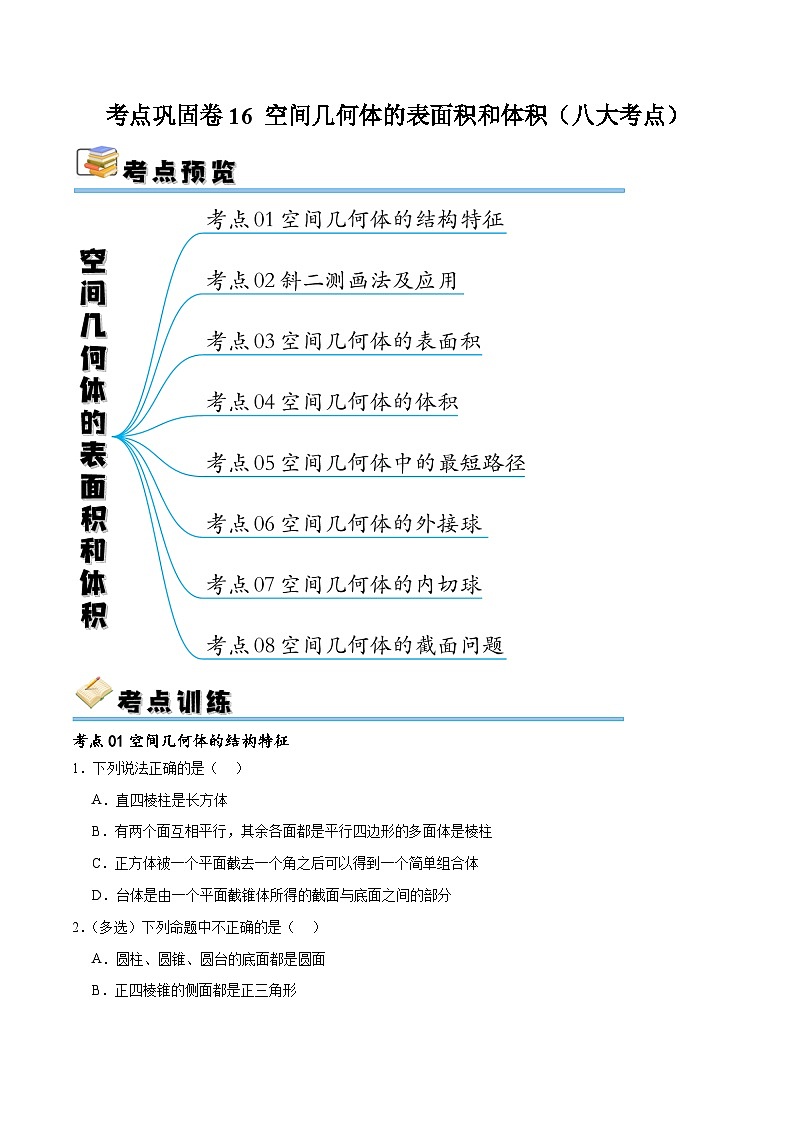


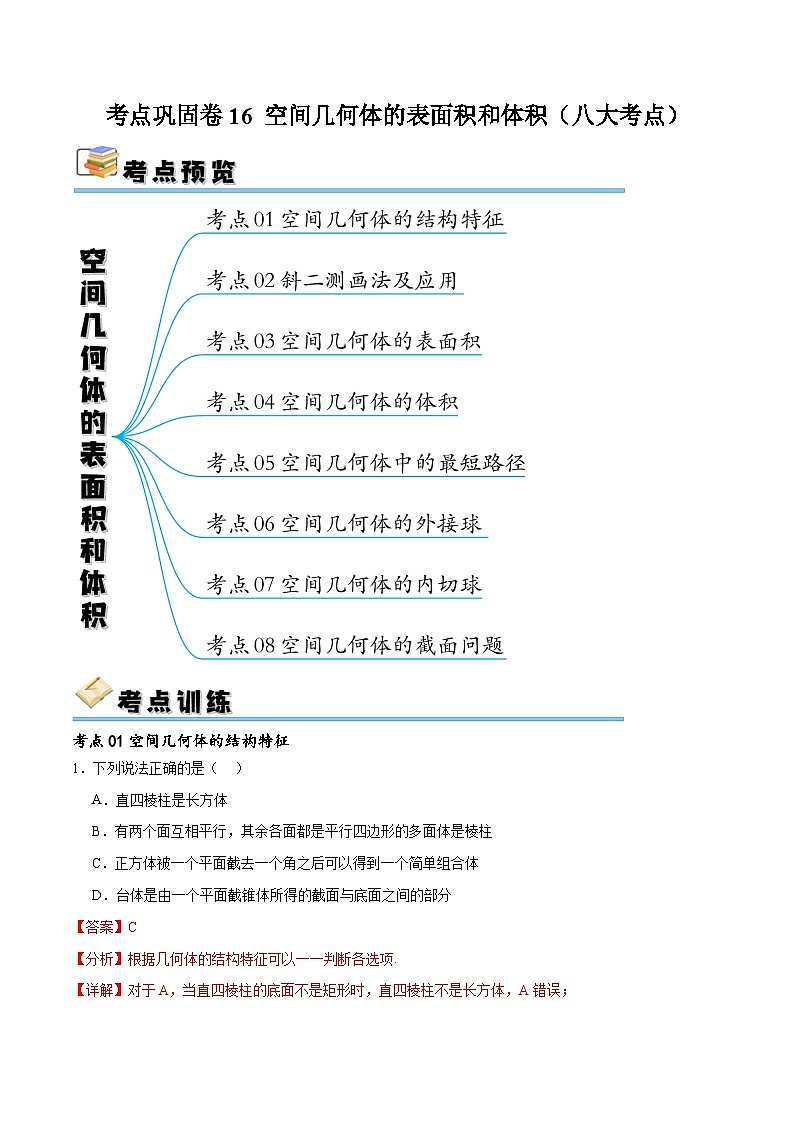


考点巩固卷16 空间几何体的表面积和体积(八大考点)-备战2024年高考数学一轮复习高分突破(新高考通用)
展开考点01空间几何体的结构特征
1.下列说法正确的是( )
A.直四棱柱是长方体
B.有两个面互相平行,其余各面都是平行四边形的多面体是棱柱
C.正方体被一个平面截去一个角之后可以得到一个简单组合体
D.台体是由一个平面截锥体所得的截面与底面之间的部分
【答案】C
【分析】根据几何体的结构特征可以一一判断各选项.
【详解】对于A,当直四棱柱的底面不是矩形时,直四棱柱不是长方体,A错误;
对于B,不符合棱柱的结构特征,如下面是一个正三棱柱,上面是一个以正三棱柱上底面为底面的斜三棱柱,B错误;
对于C,正方体被一个平面截去一个角之后可以得到一个简单组合体,C正确;
对于D,不符合台体的结构特征, 截面应该跟底面平行,D错误.
故选:C
2.(多选)下列命题中不正确的是( )
A.圆柱、圆锥、圆台的底面都是圆面
B.正四棱锥的侧面都是正三角形
C.用一个平面去截圆锥,截面与底面之间的部分是圆台
D.平行六面体的每个面都是平行四边形
【答案】BC
【分析】由正四棱锥的概念判断选项B;由旋转体的结构特征判断选项A,C;由平行六面体的特征判断选项D.
【详解】对于A,圆柱、圆锥、圆台的底面都是圆面,故选项A正确;
对于B,正四棱锥的侧面都是等腰三角形,不一定是正三角形,故选项B错误;
对于C,用平行于圆锥底面的平面去截圆锥,截面与底面之间的部分是圆台,而不是用一个平面去截圆锥,故选项C错误,
对于D,平行六面体的每个面都是平行四边形,故选项D正确,
故选:BC.
3.(多选)下列结论正确的是( )
A.等底面积、等高的两个柱体,体积相等
B.底面是正多边形的棱锥是正棱锥
C.有一个面是正方形的长方体是正四棱柱
D.用斜二测画法作水平放置的平面图形的直观图时,正方形的直观图可能还是正方形
【答案】AC
【分析】利用柱体体积公式判断A,利用正棱锥的性质判断B,利用正四棱柱的定义判断C,利用斜二测画法的要求判断D.
【详解】对于A,因为柱体的体积公式为,
所以等底面积、等高的两个柱体体积相等,故A正确;
对于B,正棱锥的侧棱相等,而底面是正多边形的棱锥,其侧棱不一定相等,故B错误;
对于C,侧棱垂直于底面,底面是正方形的棱柱是正四棱柱,
而有一个面是正方形的长方体满足上述要求,故C正确;
对于D,水平放置的正方形的直观图的邻边一定不相等,所以不可能还是正方形,故D错误.
故选:AC.
4.已知几何体,“有两个面平行,其余各面都是平行四边形”是“几何体为棱柱”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】B
【分析】利用充分条件和必要条件,结合棱柱的定义判断.
【详解】由棱柱定义知棱柱有两个面平行,其余各面都是平行四边形,故满足必要性;
但有两个面平行,其余各面都是平行四边形的几何体不一定是棱柱,
例如两个底面全等的斜棱柱拼接的几何体不是棱柱,如图所示:
,
故不满足充分性,
故选:B
5.在三棱锥中,“三棱锥为正三棱锥”是“且”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】A
【分析】验证充分性可根据正三棱锥的几何性质通过线面垂直的判定及性质判断线线垂直,必要性验证借助直四棱柱构造三棱锥满足,,结合直四棱柱的性质判断三棱锥是否为正三棱锥即可.
【详解】解:充分性:如图,在中,为中点,连接
若三棱锥为正三棱锥,则为正三角形,且,
因为为中点,所以,又平面
所以平面,又平面,则,
同理可得,故充分性成立;
必要性:如图,
在直四棱柱中,底面为菱形,且,但
由直四棱柱及底面为菱形,易得,又,
则直四棱柱的侧面均为正方形,易得,且,
由于,则不为正三角形,故三棱锥不为正三棱锥,故必要性不成立;
综上,“三棱锥为正三棱锥”是“且”的充分不必要条件.
故选:A.
考点02斜二测画法及应用
6.如图,一个水平放置的的斜二测画法的直观图是等腰直角三角形,若,则原三角形的面积为 .
【答案】
【分析】根据斜二测画法的规则,与 轴平行的线段在直观图中与轴平行,长度不变;与 轴平行的线段在直观图中与轴平行,长度减半,分别求出 的长度,即可求出面积.
【详解】根据题意可得,
在中,,
,
所以的面积为
故答案为:.
7.如图所示,梯形是平面图形用斜二测画法得到的直观图,,则平面图形中对角线的长度为( )
A.B.C.D.5
【答案】C
【分析】根据斜二测画法的规则确定原图形,利用勾股定理求得长度.
【详解】由直观图知原几何图形是直角梯形,如图,
由斜二测法则知,,,
所以.
故选:C
8.一水平放置的平面图形,用斜二测画法画出了它的直观图,该直观图是一个等腰梯形,且,则原平面图形的边 .
【答案】
【分析】分别过作于点,于点,可求出,在中求出,,从而可得,然后在直角三角形,利用勾股定理可求得结果.
【详解】分别过作于点,于点,
因为,
所以,
所以,所以,
所以,,
因为,所以为等腰直角三角形,
所以,所以,
在中,,,,
由正弦定理得,
所以,
所以,得,
所以由斜二测画法可知,,
所以,
故答案为:
9.如图,长方体的底面的斜二测直观图为平行四边形.已知,,高,,分别为,的中点,用平面截该长方体,则剩余的三棱台的体积为 .
【答案】
【分析】利用斜二测画法求出长方体的长、宽、高,再由棱台体积公式可解.
【详解】
因为,,高,
所以长方体中,,,,
又,分别为,的中点,,
由棱台体积公式.
故答案为:
10.如图所示,梯形是平面图形用斜二测画法得到的直观图,,,则 ;平面图形以所在直线为轴旋转一周所得立体图形的体积为 .
【答案】
【分析】由斜二测画法原理可得平面图形是直角梯形,进而可求;直角梯形以所在直线为轴旋转一周所得立体图形为圆台,可求其体积.
【详解】由平面图形的直观图的斜二测画法原理可知,平面图形是直角梯形,如图:
其中,,,,
过作交于,则为的中点,
在中,,,
所以;
将直角梯形以所在直线为轴旋转一周所得立体图形为圆台,
其上底面圆的半径为,下底面圆的半径为,高为,
故此圆台体积为.
故答案为:;
11.用斜二测画法画的直观图如图所示,其中,,则中边上的中线长为( )
A.B.C.D.
【答案】D
【分析】作出的原图形,结合三角形的几何性质可求得中边上的中线长.
【详解】在直观图中,,且,则,故,
又因为,则,可得,
故为等腰直角三角形,所以,,故轴,
依据题意,作出的原图形如下图所示:
延长至点,使得,则为的中点,
由题意可知,,,,且,
所以,且,故四边形为平行四边形,则,
取的中点,连接,
因为、分别为、的中点,则.
故选:D.
考点03空间几何体的表面积
12.如图,圆锥的底面直径和高均是4,过的中点作平行于底面的截面,以该截面为底面挖去一个圆柱,则剩下几何体的表面积为( )
A.B.C.D.
【答案】B
【分析】通过圆锥的底面半径和高,可求出圆柱的高和底面半径,再结合圆锥的表面积与圆柱的侧面积可求得剩下几何体的表面积.
【详解】设圆柱的高为,底面半径为,可知,
则圆锥的母线长为,
所以剩下几何体的表面积为.
故选:B.
13.如图,某几何体的形状类似胶囊,两头都是半球,中间是圆柱,其中圆柱的底面半径与半球的半径都为1,若该几何体的表面积为,则其体积为 .
【答案】
【分析】根据给定条件,求出中间圆柱的高,再利用球和圆柱的体积公式求解作答.
【详解】依题意,几何体可视为半径为1的球和底面圆半径为1,高为的圆柱组合而成,
于是几何体的表面积,解得,
所以该几何体的体积.
故答案为:
14.如图,以菱形ABCD的一边AB所在的直线为轴,其余三边旋转一周形成的面围成一个几何体,已知,.
(1)求该几何体的体积;
(2)求该几何体的表面积.
【答案】(1)
(2)
【分析】(1)根据题意可知该几何体上部分为圆锥,下部分为在圆柱内挖去一小个与上部分相同的圆锥,再根据圆柱的体积公式即可得解;
(2)根据圆柱和圆锥的侧面积公式即可得解.
【详解】(1)如图,这是所求的几何体,该几何体上部分为圆锥,下部分为在圆柱内挖去一小个与上部分相同的圆锥,
易知点D到AB的距离为,即圆柱底面圆的半径为,
所以该几何体的体积为;
(2)圆锥的侧面积为,圆柱的侧面积为,
所以该几何体的表面积为.
15.如图,将正四面体每条棱三等分,截去顶角所在的小正四面体,余下的多面体称作“阿基米德体”.若一个正四面体的棱长为12,则对应的“阿基米德体”的表面积为 .
【答案】
【分析】由阿基米德体的定义,可以得出该多面体由四个全等的正六边形和四个全等的正三角形组成,分别计算出正六边形和正三角形的面积,即可得出该几何体的表面积.
【详解】根据题意,正四面体的棱长为12,一个面的面积为,
截去顶角所在的小正四面体的边长为4,小正四面体一个面的面积为,
则该多面体中一个正六边形的面积为,
则该“阿基米德体”的表面积为.
故答案为:
16.端午节吃粽子是中华民族的传统习俗.地区不同,制作的粽子形状也不同,黔西南州最出名的就是鲜肉的灰色粽子,其形状接近于正三棱锥(如图).若正三棱锥的底面边长为2,高为1,则该三棱锥的侧面积为( )
A.B.C.D.
【答案】B
【分析】求出正三棱锥侧面三角形的高即可求解.
【详解】如图,
正三棱锥中,底面,则为正三角形的中心,
连接并延长交于,则为的中点,且,
依题意,,正三角形的边长为2,
所以,,,
,
所以该三棱锥的侧面积为.
故选:B
17.已知正四棱台上、下底面的边长分别为4和8,高为2.该正四棱台的表面积为 .
【答案】/
【分析】根据已知条件和正四棱台的特征计算侧面等腰梯形的面积,然后利用表面积的定义计算可得结果.
【详解】因为正四棱台的侧面等腰梯形,
又正四棱台的上、下底面的边长分别是4、8,高为2,
所以侧面梯形的斜高为,则梯形的面积,
上下底底面面积分别为,,
所以该四棱台的表面积为.
故答案为:.
考点04空间几何体的体积
18.如图中,,在三角形内挖去一个半圆(圆心O在边BC上,半圆与AC、AB分别相切于点C,M,交BC于点N),则图中阴影部分绕直线BC旋转一周所得旋转体的体积为 .
【答案】
【分析】根据旋转体的定义,得到图中阴影部分绕旋转一周,可得旋转体为一个圆锥挖去一个球,结合圆锥和球的体积公式,即可求解.
【详解】连接,则,
设,因为,所以,
在中,,解得,
在中,因为,可得,
设直角绕旋转一周得到的圆锥的体积为,半圆绕旋转一周得到球的体积为,图中阴影部分绕旋转一周,可得旋转体为一个圆锥挖去一个球,
所以图中阴影部分绕直线旋转一周所得旋转体的体积为:
.
故答案为:.
19.已知一个圆锥的底面半径为1,体积是,则其侧面展开图的圆心角为( )
A.B.C.D.
【答案】D
【分析】由已知条件可求出圆锥的高,从而可求出圆锥的母线长,再利用弧长公式可求得结果
【详解】设圆锥的高为,母线长为,底面半径为,侧面展开图的圆心角为,
因为圆锥的底面半径为1,体积是,
所以,得,
所以,
因为,所以,得,
即侧面展开图的圆心角为,
故选:D
20.如图,圆锥被平行于底面的一个平面所截,截去一个上、下底面半径分别为和,高为的圆台,则所得圆锥的体积为( )
A.B.C.D.
【答案】B
【分析】求出圆锥的高,利用锥体的体积公式可求得圆锥的体积.
【详解】设圆锥的高为,则,解得,
因此圆锥的体积为.
故选:B.
21.图1是宋代五大名窑中汝窑制造的双耳罐,它装物的有效部分可近似看成由两个圆台拼接而成(如图2所示)在图2中,已知下底面圆的直径是6,中间圆的直径是10,上底面圆的直径是4,上下底面圆的距离是5,且上、下两圆台的高之比是,若不考虑罐壁的厚度,则该汝窑双耳罐的容积为( )
A.B.C.D.
【答案】C
【分析】由图可知,双耳罐是由两个圆台组成,上面圆台底面半径分别为;下面圆台底面半径分别为,分别求出两个圆台的高,再利用圆台的体积公式可求得结果.
【详解】由图可知,双耳罐是由两个圆台组成,
上面圆台底面直径分别为,所以圆台底面半径分别为;
下面圆台底面直径分别为,所以圆台底面半径分别为;
又因为容器上下底面圆的距离是5,且上、下两圆台的高之比是,
所以上面圆台的高2,下面圆台的高是3,
故该汝窑双耳罐的体积为:,
.
故选:C.
22.如图,一种工业部件是由一个圆台挖去一个圆锥所制成的.已知圆台的上、下底面半径分别为和,且圆台的母线与底面所成的角为,圆锥的底面是圆台的上底面,顶点在圆台的下底面上,则该工业部件的体积为( )
A.B.C.D.
【答案】B
【分析】由题知该圆台的轴截面为等腰梯形,进而得,圆台,圆锥的高均为,再计算体积即可.
【详解】解:根据题意,该圆台的轴截面为等腰梯形,如图,
所以即为圆台母线与底面所成角,即,
分别过点、在平面内作,,垂足分别为点、,
因为,则四边形为矩形,且,
因为,,,
所以,,所以,,且,
因为,则,
所以,圆台,圆锥的高均为,
所以,该工业部件的体积为
.
故选:B.
23.如图,在正三棱柱中,,分别为,的中点.
(1)求证://平面;
(2)若,求三棱唯的体积.
【答案】(1)证明见解析
(2)
【分析】(1)解法一:构造平行四边形,根据线面平行判定定理证明即可;解法二:构造平行平面,利用面面平行的性质证明线面平行;
(2)根据几何体的线面关系确定底面积与高度距离,即可的体积.
【详解】(1)解法一:取中点,连接,,
因为是中点,所以,,
因为是中点,所以,,
所以,,
所以四边形为平行四边形,所以,
因为平面,平面,所以平面.
解法二:取中点,连接,,
因为是中点,所以,
因为平面,平面,
所以平面.
因为是中点,是中点
所以,,
所以四边形为平行四边形,所以,
因为平面,平面,
所以平面,
因为平面,平面,,
所以平面平面,
因为平面,所以平面.
(2)取中点,连接,
在正三棱柱中,
所以,且,
因为平面平面,所以,
因为,平面,平面,
所以平面,即平面,
所以的长为点到平面的距离,
又的面积为,
所以,
所以三棱锥的体积为.
考点05空间几何体中的最短路径
24.如图,某圆柱体的高为1,ABCD是该圆柱体的轴截面.已知从点B出发沿着圆柱体的侧面到点D的路径中,最短路径的长度为,则该圆柱体的侧面积是( )
A.14B.C.7D.
【答案】A
【分析】根据圆柱侧面展开图,先求出圆柱底面半径,再根据侧面积公式求圆柱体的侧面积.
【详解】
设圆柱体底面圆的半径为,将侧面的一半展开后得四边形为矩形,
则依题意得:,
所以,即,
所以该圆柱体的侧面积为:.
故选:A.
25.如图,某圆柱的一个轴截面是边长为2的正方形ABCD,点E在下底面圆周上,且,点F在母线AB上,点G是线段AC的靠近点A的四等分点,则的最小值为( )
A.B.3C.4D.
【答案】A
【分析】将绕直线AB旋转到的位置,并且点在BC的反向延长线上,连接,交AB于点,此时最小,求出即可.
【详解】将绕直线AB旋转到的位置,并且点在BC的反向延长线上,
连接,交AB于点,此时最小,如图所示:
因为,所以,
又因为,所以,
又因为,所以,
在中,由余弦定理得,
解得,即的最小值为.
故选:A.
26.如图,长方体中,,,M是的中点.
(1)求证:;
(2)求证:∥平面;
(3)点P是棱上的动点,求的最小值,并说明此时点P的位置.
【答案】(1)证明见解析
(2)证明见解析
(3),
【分析】(1)利用线面垂直的判定证明线线垂直;
(2)可以直接利用线面平行的判定定理证明,也可以先证明面面平行再利用面面平行的性质证明线面平行;
(3)将长方体侧面和沿展开,利用两点之间线段最短即可求解.
【详解】(1)连接,因为四边形为正方形,所以,
长方体中,平面,平面,
所以,
因为且平面,所以平面,
又因为平面,所以.
(2)证法一:连结交于N点,则N为的中点,
连结MN,则MN为△的中位线,故,
因为平面, 平面,所以平面;
证法二:取中点G,连接CG,则,,
所以四边形为平行四边形,所以∥,
因为平面,平面,所以∥平面,
连结,,则,,四边形GABM为平行四边形,
所以, 因为平面,平面,所以∥平面,
又因为,平面,所以平面∥平面,
又因为平面,所以∥平面,
(3)将长方体侧面和沿展开如图所示:
连接交于点,则 (当且仅当三点共线时取等号),所以即为所求点P,,
因为, 所以,即,
所以的最小值是且.
27.如图正三棱柱的底面边长为,高为2,一只蚂蚁要从顶点沿三棱柱的表面爬到顶点,若侧面紧贴墙面(不能通行),则爬行的最短路程是 .
【答案】
【分析】利用正三棱柱侧面展开图,结合两点间的最短距离是线段来求解即可.
【详解】正三棱柱的侧面部分展开图如图所示,
图1,连接与交于点,则爬行的最短路程时沿着爬行,
此时,
图2,连接,过作AB的垂线交于点,则,
则,所以,
∵,∴爬行的最短路程是.
故答案为:.
28.已知在直角三角形中,,(如图所示)
(1)若以为轴,直角三角形旋转一周,求所得几何体的表面积.
(2)一只蚂蚁在问题(1)形成的几何体上从点绕着几何体的侧面爬行一周回到点,求蚂蚁爬行的最短距离.
【答案】(1)
(2)
【分析】(1)若以为轴,直角三角形旋转一周,形成的几何体为以为半径,高的圆锥,由圆锥的表面积公式,即可求出结果.
(2)利用侧面展开图,要使蚂蚁爬行的最短距离,则沿点B的母线把圆锥侧面展开为平面图形(如图)最短距离就是点B到点的距离,代入数值,即可求出结果.
【详解】(1)在直角三角形中,由
即,得,若以为轴旋转一周,
形成的几何体为以为半径,高的圆锥,
则,其表面积为.
(2)由问题(1)的圆锥,要使蚂蚁爬行的最短距离,
则沿点的母线把圆锥侧面展开为平面图形,
最短距离就是点到点的距离,,
在中,由余弦定理得.
29.圆锥的母线,高为,点是的中点,一质点自点出发,沿侧面绕行一周到达点的最短路程为 .
【答案】
【分析】作出圆锥侧面展开图,可知所求最短路程为,结合扇形弧长公式、余弦定理可求得结果.
【详解】将圆锥的侧面展开,连接,
则的长即为质点绕行的最短路程,由题设易知:圆锥底面半径为2;
在中,,,弧长,;
利用余弦定理得:,;
质点自点出发,沿侧面绕行一周到达点的最短路程为.
故答案为:.
考点06空间几何体的外接球
30.在三棱锥中,面,为等边三角形,且,则三棱锥的外接球的表面积为 .
【答案】
【分析】由已知结合三棱锥和正三棱柱的几何特征,可得此三棱锥外接球,即为以为底面以为高的正三棱柱的外接球,分别求出棱锥底面半径r和球心距d,可得球的半径R,即可求出三棱锥外接球的表面积.
【详解】因为是直三棱锥,底面是正三角形,所以可以将图补形成为正三棱柱,如图所示,
此三棱锥外接球,即为以为底面以为高的正三棱柱的外接球,
设球心为O,作平面,则为的外接圆圆心,连接,则,
设的外接圆半径为r,三棱锥外接球半径为R,
由正弦定理,得,所以,
中,,所以,解得,
所以.
故答案为:.
31.如图,长方体中,,则四面体的外接球的体积为 .
【答案】
【分析】四面体的外接球与长方体的外接球是同一个球,可求出外接球的半径,进而得体积.
【详解】,,,
四面体的外接球与长方体的外接球是同一个球,
其半径为,其体积为.
故答案为:.
32.如图,在三棱锥的平面展开图中,,,,,,则①的余弦值为 ;②三棱锥外接球的表面积为 .
【答案】 /
【分析】根据题意求得的长,在中,由余弦定理求得的值,再由球的截面圆的性质,列出方程求得三棱锥外接球的半径为,结合球的表面积公式,即可求解.
【详解】在中,因为,,所以,所以.
在中,因为,,,
所以,所以.
又因为,
所以在中,由余弦定理得
,
设的外接圆的半径为,且外接圆的圆心为,
可得,所以,
设三棱锥外接球的半径为,且外接球的球心为,
在直角中,可得,
即,所以,
所以外接球的表面积为.
故答案为:;.
33.在矩形中,,为的中点,将和沿,翻折,使点与点重合于点,若,则三棱锥外接球的表面积为( )
A.B.C.D.
【答案】B
【分析】先证明出MP⊥平面PAD,设△ADP的外接圆的半径为r, 三棱锥M-PAD的外接球的半径为R,由,求出R,进而求出外接球的表面积.
【详解】由题意可知,.
又平面PAD,平面PAD,所以MP⊥平面PAD.
设△ADP的外接圆的半径为r,则由正弦定理可得,即,
所以,设三棱锥M-PAD的外接球的半径为R,则,
所以外接球的表面积为.
故选:B
34.在四面体PABC中,,是边长为2的等边三角形,若二面角的大小为,则四面体的外接球的表面积为( )
A.B.C.D.
【答案】C
【分析】先根据题意,作出四面体的外接球的球心大致位置,再根据二面角的定义求得,从而在中求得,结合勾股定理即可求得外接球的半径,由此得解.
【详解】设正的重心为,则是正的外接圆的圆心,
取的中点, 因为,所以是的外接圆的圆心,
过作平面,过作平面,,如图,
则为四面体的外接球的球心,
又二面角的大小为,则,
又在正中,,
则在中,,
设四面体PABC的外接球的半径为,
则,
所以四面体PABC的外接球的表面积为.
故选:C.
35.在矩形中,,,点E,F分别为BC,AD的中点,点H为AE的中点,将沿直线AE翻折至的位置,当时,三棱锥的外接球的体积是 .
【答案】
【分析】首先利用几何关系,找到球的球心,再根据球的半径求三棱锥外接球的体积.
【详解】因为在矩形中,,,点E,F分别为BC,AD的中点,
所以,为等腰直角三角形,
如图,由题可知点F为的外心,过点F作直线l,使l⊥平面ABCD.
又H点为的外心,过H点作⊥平面.
交l于O点,则点O为球心,设球的半径为,
易知,则,
在中:.
所以球的体积为.
故答案为:
考点07空间几何体的内切球
36.已知圆锥的顶点为,轴截面为锐角,,则当 时,圆锥的内切球与外接球的表面积的比值最大,最大值为 .
【答案】 / /
【分析】作出图形,设,,为线段的中点,连接,设圆锥的内切球和外接球的半径分别为、,计算出、关于的表达式,结合二次函数的基本性质可求得的最大值及其对应的值,即可得解.
【详解】如下图所示:
不妨设,,为线段的中点,
连接,圆锥的内切球球心为,半径为;外接球球心为,半径为.
圆锥的内切球与外接球的表面积之比为,
在中,,,
,
在中,,,,
即,所以,,
所以,
,
当且仅当时,即当时,等号成立,
所以,圆锥的内切球与外接球的表面积的比值的最大值为.
故答案为:;.
37.已知三棱锥P-ABC的所有顶点均在半径为2的球的O球面上,底面是边长为3的等边三角形.若三棱锥P-ABC的体积取得最大值时,该三棱锥的内切球的半径为r,则( )
A.1B.C.D.
【答案】B
【分析】设底面的中心为Q,根据题意可知,当三棱锥P-ABC的体积取得最大值时,底面ABC,求出体积的最大值,再利用等体积法求出内切球的半径即可.
【详解】设底面的中心为Q,连接BQ,OQ,
则,且底面ABC,
如图,延长QO交球面于点P,连接OB,此时三棱锥P-ABC的体积取得最大值,
因为球O的半径为2,所以,
在中,,
所以三棱锥P-ABC的体积的最大值为,
此时,
所以,
所以,解得.
故选:B.
38.已知球内切于圆台(即球与该圆台的上、下底面以及侧面均相切),且圆台的上、下底面半径,则圆台的体积与球的体积之比为( )
A.B.C.2D.
【答案】B
【分析】画出圆台的轴截面图,由几何知识可确定球的半径,即可得答案.
【详解】如图为该几何体的轴截面,其中圆是等腰梯形的内切圆,设圆与梯形的腰相切于点,与上、下底的分别切于点,,
设球的半径为,圆台上下底面的半径为,.注意到与均为角平分线,因此,
从而,故.设台体体积为,球体体积为,
则.
故选:B
39.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.在鳖臑中,平面,,且,则其内切球表面积为( )
A.B.C.D.
【答案】C
【分析】设四面体内切球的球心为,半径为,则,求得,,从而求得,根据球的表面积公式即可求解.
【详解】
因为四面体四个面都为直角三角形,平面,
所以,,
设四面体内切球的球心为,半径为,
则
所以,
因为四面体的表面积为,
又因为四面体的体积,
所以,
所以内切球表面积.
故选:C.
40.校考期末)一个正四面体的棱长为2,则它的外接球与内切球体积之比为( )
A.B.C.D.
【答案】D
【分析】作出辅助线,求出外接球和内切球的半径,从而得到体积之比.
【详解】正四面体中,取中点,连接,则⊥,
过点作⊥于点,
则⊥平面,外接球球心在上,连接,则,
因为正四面体的棱长为2,所以,,
则,,
,
由勾股定理得,即,
解得,
设内切球球心为,则在上,过点作⊥于点,则,
故,,
因为∽,所以,即,
解得,
故它的外接球与内切球半径之比为,体积之比为.
故选:D
41.正四棱锥中,底面边长,侧棱,在该四棱锥的内部有一个小球,则小球表面积的最大值为( )
A.B.C.D.
【答案】D
【分析】当小球与正四棱锥各面相切时半径最大,此时小球表面积的最大,计算求解即可.
【详解】当小球与正四棱锥各面相切时半径最大,此时小球表面积的最大,
设小球的半径为,
由底面边长,侧棱,可得正四棱锥的高,
所以,
又侧面面积为,底面面积为,
,解得,
小球表面积的最大值为.
故选:D.
考点08空间几何体的截面问题
42.用一个平面去截一个正方体,所得截面形状可能为:( )
①三角形②四边形③五边形④六边形⑤圆
A.①②③B.①②④C.①②③④D.①②③④⑤
【答案】C
【分析】由正方体的结构特征,作出截面即可判断.
【详解】用一个平面去截一个正方体,分别是所在棱的中点,所得截面形状可能为三角形、四边形、五边形、六边形,
如图所示:
故选:C.
43.在正四棱台中,,侧棱,若为的中点,则过,,三点截面的面积为( )
A.B.C.D.
【答案】A
【分析】取的中点,则,又,则,可得过,,三点截面为等腰梯形,利用题中数据及正四棱台的性质计算即可.
【详解】
取的中点,连接,则,
又,则,又根据正四棱台的性质得,
则为等腰梯形,即过,,三点截面为等腰梯形.
取的中点,连接,
在等腰梯形中,,
则,,
在等腰梯形中,,,
则梯形的高为,
所以等腰梯形的面积.
故选:A.
44.如图所示的一块长方体木料中,已知,设E为底面ABCD的中心,且,则该长方体中经过点的截面面积的最小值为 .
【答案】
【分析】作出辅助线,得到平行四边形即为该长方体中经过点的截面,建立空间直角坐标系,利用点到直线距离公式表达出截面面积,求出最值.
【详解】连接并延长,交于点,过点作平行于交于点,
连接,则平行四边形即为该长方体中经过点的截面,
以为坐标原点,所在直线分别为轴,建立空间直角坐标系,
则,,,则,
故点到直线的距离为
,
则截面面积为
,
因为,所以当时,取得最小值,
故截面面积最小值为
故答案为:
45.如图,在三棱锥木块中,VA,VB,VC两两垂直,,点P为的重心,沿过点P的平面将木块锯开,且使截面平行于直线VC和AB,则该截面的面积为 .
【答案】
【分析】如图作出平面,根据线面平行的判定定理,可证平面,平面,则平面即为所求,根据线面平行的判定定理、性质定理,可证四边形为平行四边形,根据线面垂直的判定定理、性质定理,可证四边形为矩形,根据三角形相似,可求得的值,即可得答案.
【详解】由VA,VB,VC两两垂直,,
则可将三棱锥补形到正方体中,连接AP并延长,交VC于D,过P作VC的平行线,交AV于E,交AC与F,过E作,交VB于H ,过H作,交BC于M,连接MF,如图所示
因为,所以E、F、M、H四点共面,
因为,平面,平面,
所以平面,
因为,平面,平面,
所以平面,
则平面即为所求,
因为,平面,平面,
所以平面,
又平面,平面平面,
所以,
所以四边形为平行四边形,
又,平面VAB,
所以平面VAB,
所以平面VAB,
因为平面VAB,
所以,即四边形为矩形,
因为,
所以,
因为P为的重心,
所以,则,
同理可证,
所以,则,
所以矩形的面积为
故答案为:
46.已知四棱锥中,平面ABCD,四边形ABCD为正方形,,平面过PB,BC,PD的中点,则下列关于平面截四棱锥所得的截面正确的为( )
A.所得截面是正五边形B.截面过棱PA的三等分点
C.所得截面面积为D.截面不经过CD中点
【答案】C
【分析】根据给定条件,作出平面截四棱锥所得的截面多边形,再逐一判断各选项即可.
【详解】
在四棱锥中,,取中点分别为,连接,FG,GH,BD,AC,如图,
因底面为正方形,E,F,H分别是棱PB,BC, PD的中点,
则,所以四边形EFGH是平行四边形.
对于A,令,有 ,在P A上取点,使,
连接EI,HI,JI,则,
因为点平面EFGH,有平面EFGH,
所以点平面 平面EFGH,
因此五边形EFGHI是平面截四棱锥所得的截面多边形,
而,
所以截面不是正五边形,A错误;
对于B,由A选项分析,可知截面过棱PA的四等分点,B错误;
对于C,底面平面,则,
而,则,
又平面,因此平面 平面,
于是得,有,
所以矩形EFGH面积等于,
而,则边EH上的高等于,
所以,
所以截面五边形EFGHI面积为, C正确;
对于D,截面经过CD中点,D错误.
故选:C
47.校考期末)如图,棱长为2的正方体中,,分别为棱,的中点,
(1)求作过,,三点的截面(写出作图过程);
(2)求截面图形的面积
【答案】(1)作图见解析;
(2).
【分析】(1)画直线,借助平面基本事实确定截面多边形顶点位置即可.
(2)由(1)的作图,利用割补法求出截面面积作答.
【详解】(1)在正方体中,画直线与的延长线分别交于点,
连接,分别与棱交于点,连接,如图1,
抹去和得过三点的正方体的截面五边形,如图2.
(2)在正方体中,,,分别为棱,的中点,
由(1)及图1知,,即,,则,
,等腰底边上的高,
的面积,
由,得,即有,因此,
于是,同理,
所以截面五边形的面积.
考点巩固卷19 直线与圆(十二大考点)-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份考点巩固卷19 直线与圆(十二大考点)-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含考点巩固卷19直线与圆十二大考点原卷版docx、考点巩固卷19直线与圆十二大考点解析版docx等2份试卷配套教学资源,其中试卷共67页, 欢迎下载使用。
考点巩固卷17 空间中的平行与垂直(八大考点)-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份考点巩固卷17 空间中的平行与垂直(八大考点)-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含考点巩固卷17空间中的平行与垂直八大考点原卷版docx、考点巩固卷17空间中的平行与垂直八大考点解析版docx等2份试卷配套教学资源,其中试卷共83页, 欢迎下载使用。
考点巩固卷15 等比数列(八大考点)-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份考点巩固卷15 等比数列(八大考点)-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含考点巩固卷15等比数列八大考点原卷版docx、考点巩固卷15等比数列八大考点解析版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。












