



- 专题4.2 圆切线的判定与性质综合(3大类题型)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版) 试卷 0 次下载
- 专题4.3 圆中利用转化思想求角度(4大类题型)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版) 试卷 0 次下载
- 专题4.5 线圆最值(隐圆压轴二)(题型专练)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版) 试卷 0 次下载
- 专题4.6 阿氏圆(隐圆压轴三)(题型专练)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版) 试卷 0 次下载
- 专题4.7 定弦定角(隐圆压轴四)(题型专练)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版) 试卷 0 次下载
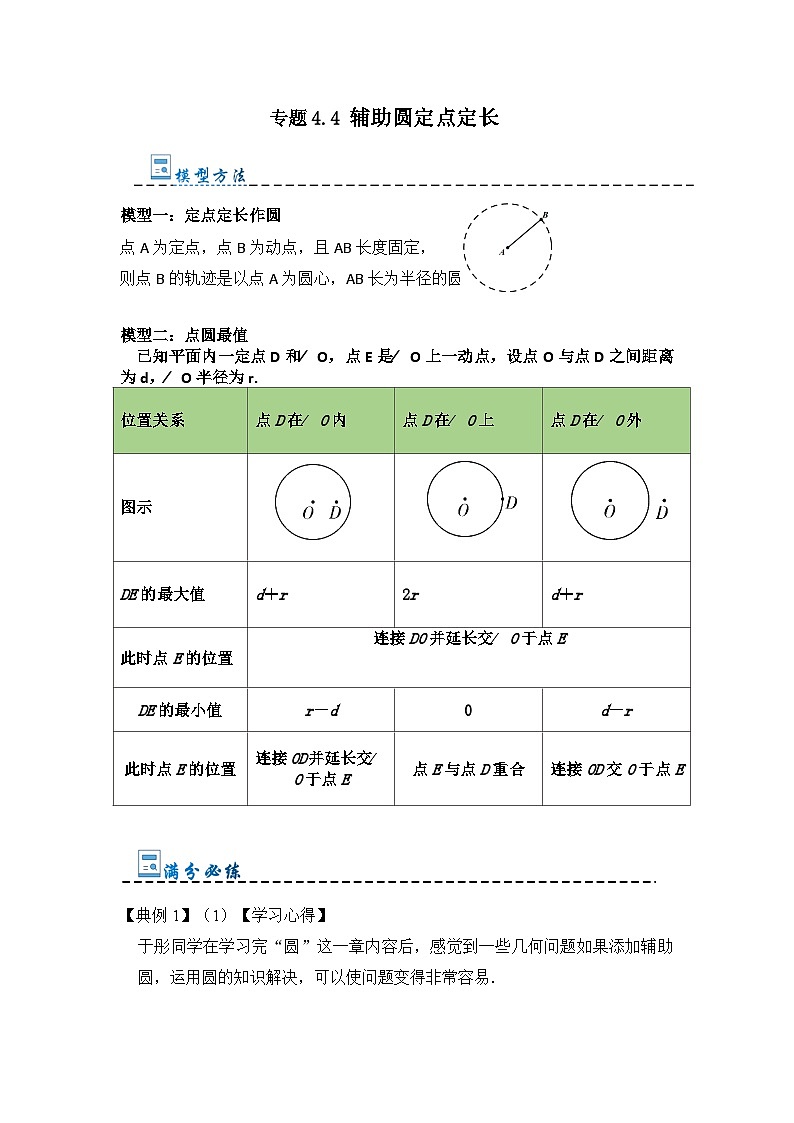
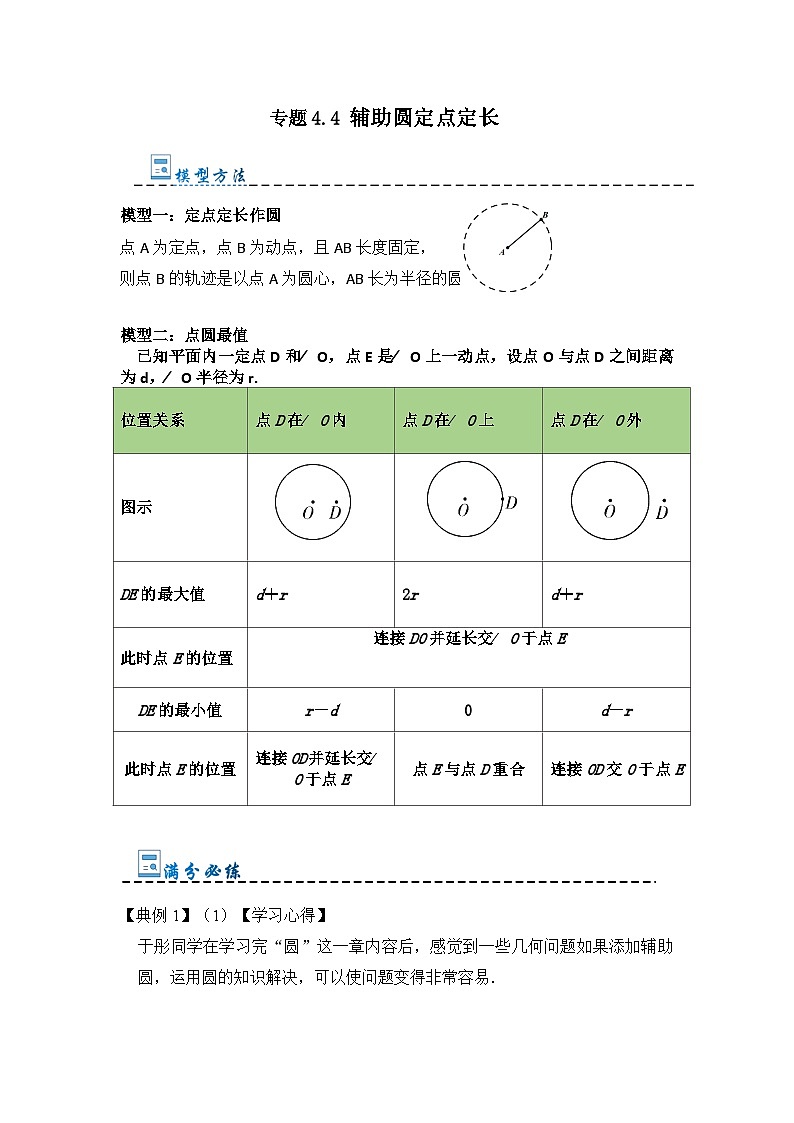
专题4.4 辅助圆定点定长(题型专练)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版)
展开模型一:定点定长作圆
点A为定点,点B为动点,且AB长度固定,
则点B的轨迹是以点A为圆心,AB长为半径的圆。
模型二:点圆最值
已知平面内一定点D和O,点E是O上一动点,设点O与点D之间距离为d,O半径为r.
【典例1】(1)【学习心得】
于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC= °.
(2)【问题解决】
如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.
(3)【问题拓展】
如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
【变式1-1】如图,在四边形ABCD中,AB=AC=AD,∠CAD=2∠BAC,若∠BCD=105°,则∠BDC= .
【变式1-2】如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
A.68°B.88°C.90°D.112°
【变式1-3】如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD= 度.
【变式1-4】如图,四边形ABCD中,AB=AC=AD,∠CBD=20°,∠BDC=30°,则∠BAD= .
【变式1-5】如图,在四边形ABCD中,AC、BD是对角线,AB=AC=AD,如果∠BAC=70°,那么∠BDC= .
【变式1-6】如图(1),在Rt△ABC中,∠A=90°,AB=AC=4,D、E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为a(0°<a≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;
(2)当∠CPD1=2∠CAD1时,则旋转角为a= (直接写结果)
(3)连接PA,△PAB面积的最大值为 (直接写结果)
【典例2】如图,在△ABC中,点D是边BC的中点,点E是边AC上的任意一点(点E不与点C重合),沿DE翻折△DCE使点C落在点F处,请画出点F的轨迹.
【变式2-1】如图,在▱ABCD中,AE⊥BC于点E,将△AEB绕点B顺时针旋转,使AB与边BC重合,得到△MNB,请画出在旋转过程中点M的运动轨迹.
【变式2-2】如图,在Rt△ABC中,∠ABC=90°,AB=4,D是BC边上一动点,将△ABD沿AD对折,得到△AB'D,当点B'落在AC边上时,点D停止运动,若AB'=AC,则在点D的运动过程中,点B'的运动路径长为 .
【变式2-3】如图,在菱形ABCD中,∠ABC=60°,BC=3,将菱形ABCD绕点B逆时针旋转,得到菱形A'BC'D',求出当点D'在BA的延长线上时,点C'运动的路径长.
【典例3】如图,在矩形ABCD中,,,E是AB边的中点,F是线面BC边上的动点,将沿EF所在的直线折叠得到,连接,求的最小值。
【变式3-1】如图,正方形ABCD的边长为6,点E是边BC上一动点,点F在边CD上,BF⊥AE,则CG的最小值为 .
【变式3-2】(锦州)如图,在矩形ABCD中,AB=3,BC=2,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△A′MN,连接A′C,则A′C的最小值是 .
【变式3-3】如图,矩形ABCD中,AB=4,BC=8,P是直线AB上的一个动点,AE=2,△APE沿PE翻折形成△FPE,连接PF、EF,则FC的最小值是 ,点F到线段BC的最短距离是 .
【变式3-4】(2022•武功县模拟)如图,在矩形ABCD中,AB=6,BC=5,点E在BC上,且CE=4BE,点M为矩形内一动点,使得∠CME=45°,连接AM,则线段AM的最小值为 .
【变式3-5】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,点E是AC的中点,点F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,则△BDF周长的最小值是 .
【典例4】(邗江区期末)如图,在平面直角坐标系xOy中,已知点A(1,0),B(3,0),C为平面内的动点,且满足∠ACB=90°,D为直线y=x上的动点,则线段CD长的最小值为( )
A.1B.2C.D.
【变式4-1】(武江区校级期末)如图,⊙M的半径为4,圆心M的坐标为(5,12),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为 .
【变式4-2】(萨尔图区校级期末)如图,点A,B的坐标分别为A(4,0),B(0,4),C为坐标平面内一点,BC=2,点M为线段AC的中点,连接OM,OM的最大值为 .
【变式4-3】(2022•鱼峰区模拟)如图,⊙M的半径为2,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最大值为 .
【变式4-4】如图,点A,B的坐标分别为A(4,0),B(0,4),C为坐标平面内一点,BC=2,点M为线段AC的中点,连接OM,OM的最大值为 .
位置关系
点D在O内
点D在O上
点D在O外
图示
DE的最大值
d+r
2r
d+r
此时点E的位置
连接DO并延长交O于点E
DE的最小值
r-d
0
d-r
此时点E的位置
连接OD并延长交O于点E
点E与点D重合
连接OD交O于点E
备战中考数学《重难点解读•专项训练》专题01 辅助圆定点定长(知识解读): 这是一份备战中考数学《重难点解读•专项训练》专题01 辅助圆定点定长(知识解读),共13页。试卷主要包含了复习方法,复习难点等内容,欢迎下载使用。
备战中考数学《重难点解读•专项训练》专题01 辅助圆定点定长(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题01 辅助圆定点定长(专项训练),文件包含专题01辅助圆定点定长专项训练原卷版docx、专题01辅助圆定点定长专项训练解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
专题4.8 四点共圆(隐圆压轴五)(题型专练)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版): 这是一份专题4.8 四点共圆(隐圆压轴五)(题型专练)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版),文件包含专题48四点共圆隐圆压轴五题型专练原卷版docx、专题48四点共圆隐圆压轴五题型专练解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。












