专题4.8 四点共圆（隐圆压轴五）（题型专练）-2023-2024学年九年级数学上册期末复习《重难点题型》（人教版）

这是一份专题4.8 四点共圆（隐圆压轴五）（题型专练）-2023-2024学年九年级数学上册期末复习《重难点题型》（人教版），文件包含专题48四点共圆隐圆压轴五题型专练原卷版docx、专题48四点共圆隐圆压轴五题型专练解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

1.四点共圆
如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”．
2．四点共圆的性质
(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等．
(2)圆内接四边形的对角互补．
(3)圆内接四边形的一个外角等于它的内对角．
3．四点共圆的判定
(1)用“角”判定：
①一组对角互补的四边形的四个顶点在同一个圆上；
②一个外角等于它的内对角的四边形的四个顶点在同一个圆上；
③如果两个三角形有一条公共边，且位于公共边同侧的两个角相等，则这两个三角形的四个顶点在同一个圆上．
(2)“等线段”判定：
四顶点到同一点的距离相等，若OA＝OB＝OC＝OD，则A，B，C，D四点共圆．
(3)用“比例线段”判定：
若线段AB，CD(或其延长线)交于点P，且PA·PC＝PB·PD，则A，B，C，D四点共圆.
模型解读：
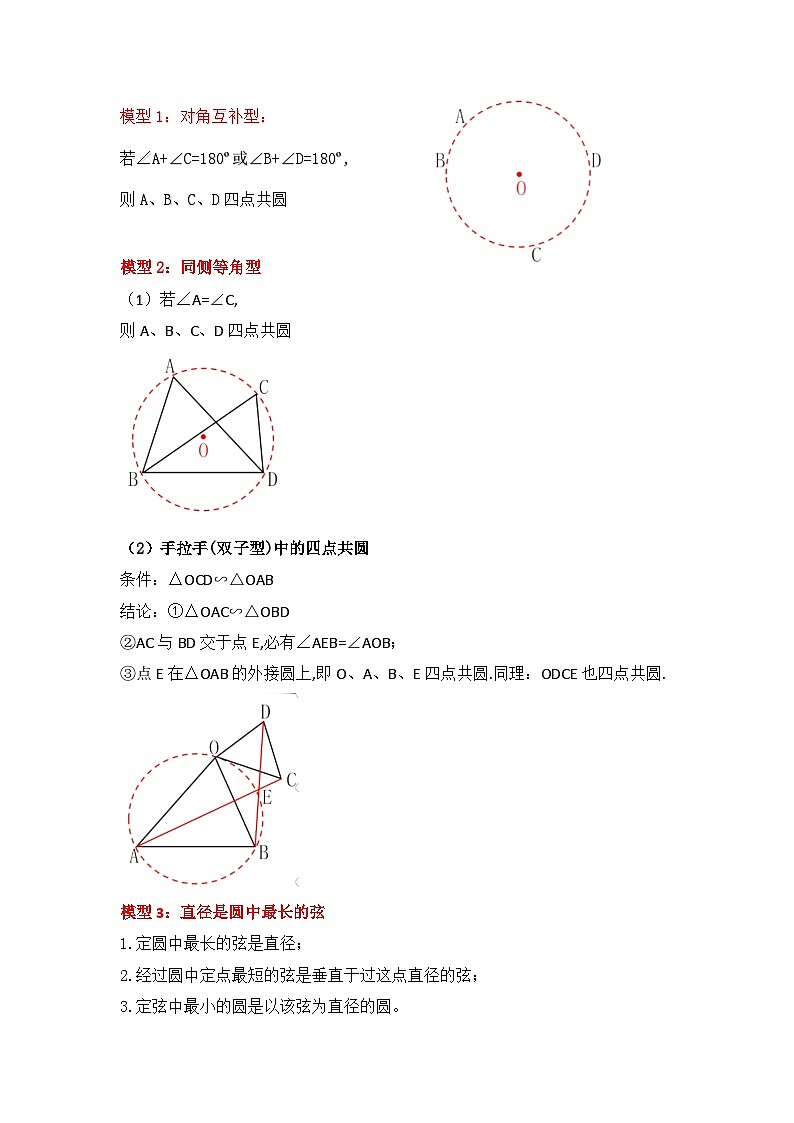
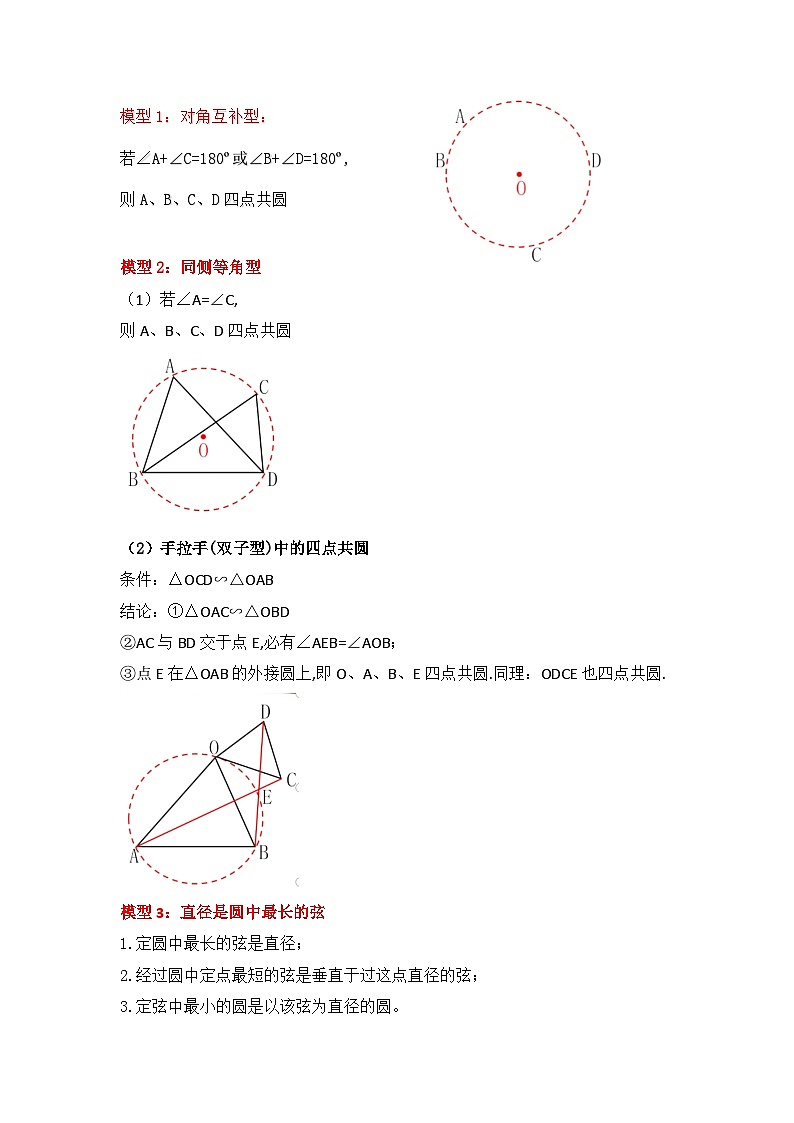
模型1：对角互补型：
若∠A+∠C=180º或∠B+∠D=180º,
则A、B、C、D四点共圆
模型2：同侧等角型
（1）若∠A=∠C,
则A、B、C、D四点共圆
（2）手拉手(双子型)中的四点共圆
条件：△OCD∽△OAB
结论：①△OAC∽△OBD
②AC与BD交于点E,必有∠AEB=∠AOB；
③点E在△OAB的外接圆上,即O、A、B、E四点共圆.同理：ODCE也四点共圆.
模型3：直径是圆中最长的弦
1.定圆中最长的弦是直径；
2.经过圆中定点最短的弦是垂直于过这点直径的弦；
3.定弦中最小的圆是以该弦为直径的圆。

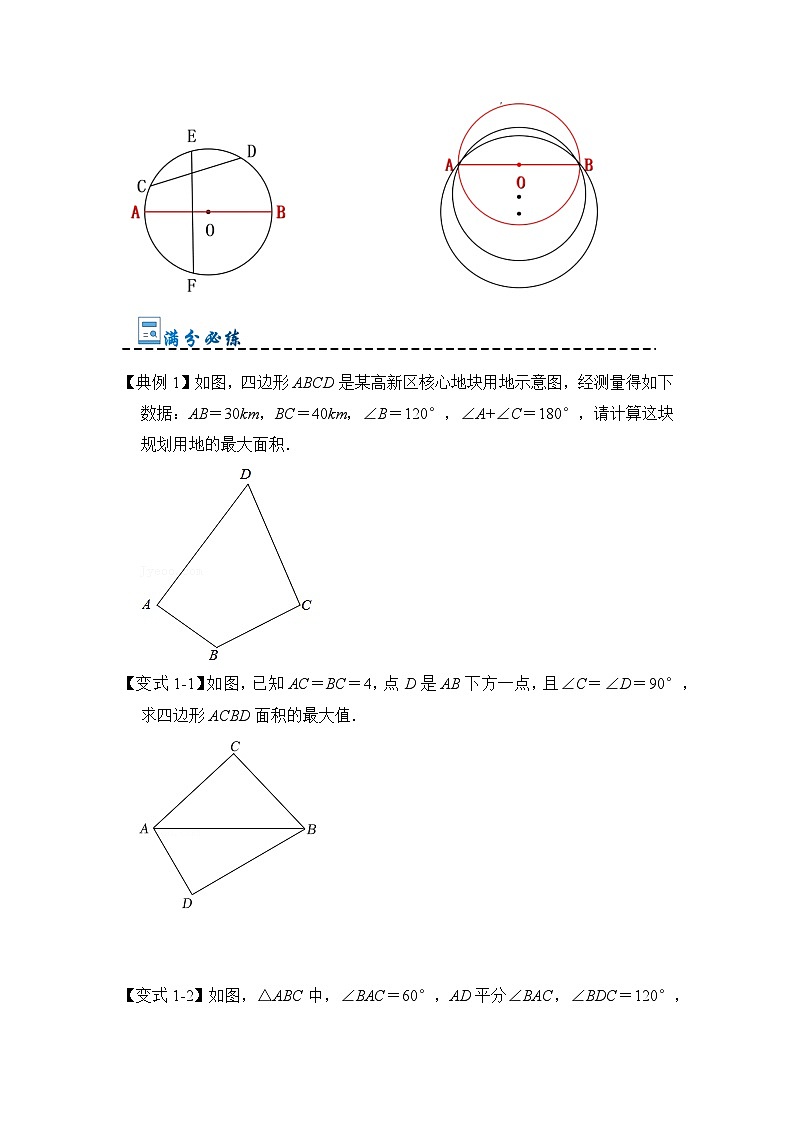
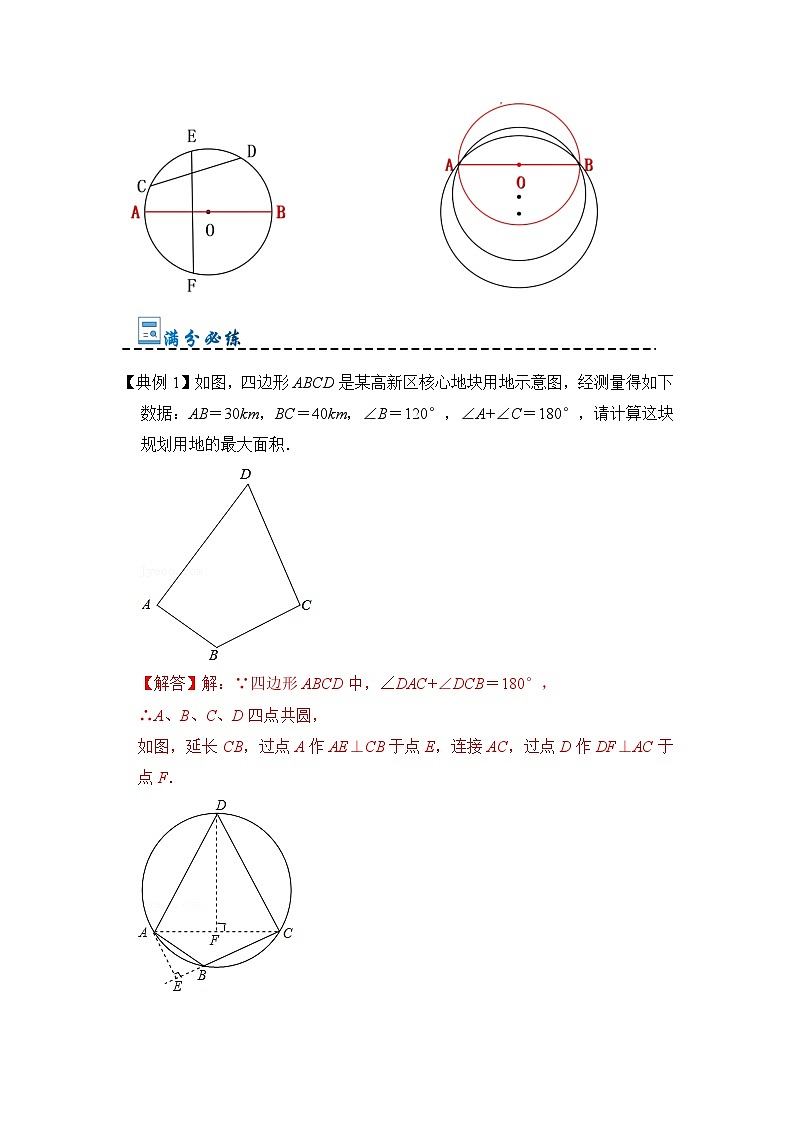
【典例1】如图，四边形ABCD是某高新区核心地块用地示意图，经测量得如下数据：AB＝30km，BC＝40km，∠B＝120°，∠A+∠C＝180°，请计算这块规划用地的最大面积．
【变式1-1】如图，已知AC＝BC＝4，点D是AB下方一点，且∠C＝∠D＝90°，求四边形ACBD面积的最大值．
【变式1-2】如图，△ABC中，∠BAC＝60°，AD平分∠BAC，∠BDC＝120°，连接BD，CD并延长分别交AC，AB于点E和点F，若DE＝6，，则BD的长为（ ）
A．10B．12C．15D．16
【变式1-3】如图，△ABC中，∠ACB＝90°，点D为边AB的中点，△ADC沿直线CD翻折至△ABC所在平面内得△A′DC，AA′与CD交于点E．若，，则点A′到AB的距离是（ ）
A．B．C．D．
【变式1-4】如图，正方形ABCD和正方形DEFG边长分别为a和b，正方形DEFG绕点D旋转，给出下列结论：①AG＝CE；②AG⊥CE；③点G、D、H、E四点共圆；④DH平分∠ADE；⑤AC2+EG2＝CG2+AE2，其中正确的结论是（ ）
A．①②③B．①②④C．①③④D．①②③⑤
【变式1-5】如图，AB＝AD＝6，∠A＝60°，点C在∠DAB内部且∠C＝120°，则CB+CD的最大值（ ）
A．4B．8C．10D．6
【变式1-6】如图，在等腰三角形纸片ABC中，AB＝AC，将该纸片翻折，使得点C落在边AB的F处，折痕为DE，D，E分别在边BC，AC上，∠AFD＝∠DEF，若DE＝4，BD＝9，则DF＝ ，△ABC的面积为 ．
【变式1-7】如图，以C为公共顶点的Rt△ABC和Rt△CED中，∠ACB＝∠CDE＝90°，∠A＝∠DCE＝30°，且点D在线段AB上，则∠ABE＝ ，若AC＝10，CD＝9，则BE＝ ．
【变式1-8】如图，AB⊥BC，AB＝5，点E、F分别是线段AB、射线BC上的动点，以EF为斜边向上作等腰Rt△DEF，∠D＝90°，连接AD，则AD的最小值为 ．
【变式1-9】【问题情境】如图①，在四边形ABCD中，∠B＝∠D＝90°，求证：A、B、C、D四点共圆．
小吉同学的作法如下：连结AC，取AC的中点O，连结OB、OD，请你帮助小吉补全余下的证明过程；
【问题解决】如图②，在正方形ABCD中，AB＝2，点E是边CD的中点，点F是边BC上的一个动点，连结AE，AF，作EP⊥AF于点P．
（1）如图②，当点P恰好落在正方形ABCD对角线BD上时，线段AP的长度为 ；
（2）如图③，过点P分别作PM⊥AB于点M，PN⊥BC于点N，连结MN，则MN的最小值为 ．
【变式1-10】如图，在Rt△ABC中，∠BAC＝90°，∠ABC＝40°，将△ABC绕A点顺时针旋转得到△ADE，使D点落在BC边上．
（1）求∠BAD的度数；
（2）求证：A，D，B，E四点共圆．