高中数学北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值教案配套课件ppt

这是一份高中数学北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值教案配套课件ppt，共36页。PPT课件主要包含了新知初探·课前预习，题型探究·课堂解透，平均水平，答案A，答案C，答案036，答案2376，易错警示，答案B，答案09等内容，欢迎下载使用。

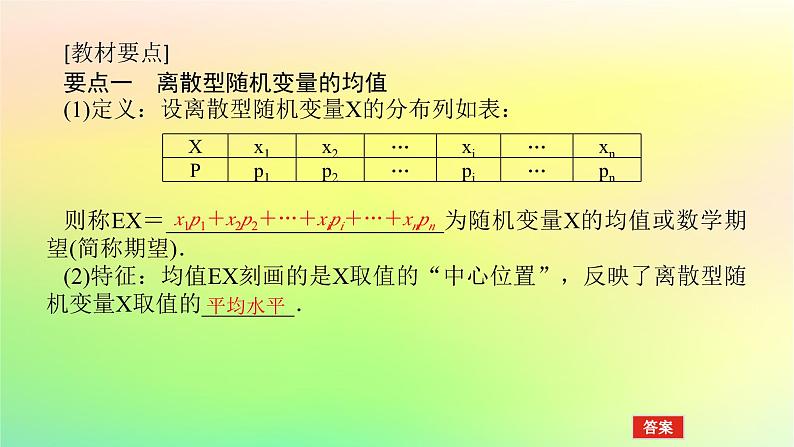
[教材要点]要点一　离散型随机变量的均值(1)定义：设离散型随机变量X的分布列如表：则称EX＝________________________为随机变量X的均值或数学期望(简称期望)．(2)特征：均值EX刻画的是X取值的“中心位置”，反映了离散型随机变量X取值的________．
x1p1＋x2p2＋…＋xipi＋…＋xnpn
状元随笔　1.均值是算术平均值概念的推广，是概率意义下的平均数．2．离散型随机变量的均值EX是一个数值，是随机变量X本身固有的一个数字特征，它不具有随机性，反映的是随机变量取值的平均水平．3．由离散型随机变量的均值的定义可知，它与离散型随机变量有相同的单位．
要点二　两点分布的均值若X服从参数为P的两点分布，则EX＝P.
[基础自测]1．思考辨析(正确的画“√”，错误的画“×”)(1)随机变量X的均值EX是一个变量，它随样本的改变而改变．(　　)(2)随机变量的均值相同，则两个分布也一定相同．(　　)(3)常数的数学期望就是这个常数本身．(　　)(4)若X服从两点分布，则EX＝np.(　　)
2．已知随机变量ξ满足P(ξ＝1)＝0.3，P(ξ＝0)＝0.7，则Eξ＝(　　)A．0.3 B．0.6C．0.7 D．1
解析：因为随机变量ξ服从两点分布，且P(ξ＝1)＝0.3，所以Eξ＝0.3.故选A.
3．随机抛掷一枚骰子，则所得骰子点数ξ的均值是(　　)A．0.6 B．1C．3.5 D．2
解析：抛掷骰子所得点数ξ的分布列为
4．已知某一随机变量X的分布列如下表：且EX＝6，则a＝________，b＝________．
解析：由0.2＋0.5＋a＝1，得a＝0.3.又由EX＝3×0.2＋b×0.5＋8×a＝6，得b＝6.
题型一　利用分布列的性质求均值例1　设ξ是一个离散型随机变量，其分布列如下表，试求Eξ
方法归纳根据分布列的性质求参数，再由均值的定义求解．
跟踪训练1　已知随机变量X的分布列如表：求EX.
题型二　求离散型随机变量的均值例2　一个盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3.从盒中任取3张卡片．(1)求所取3张卡片上的数字完全相同的概率；(2)X表示所取3张卡片上的数字的中位数，求X的分布列与数学期望．(注：若三个数a，b，c满足a≤b≤c，则称b为这三个数的中位数)
方法归纳求离散型随机变量X的均值的步骤：(1)理解X的实际意义，并写出X全部可能的取值；(2)求出X取每个值时的概率；(3)写出X的分布列(有时也可省略)；(4)利用定义公式EX＝x1p1＋x2p2＋…＋xipi＋…＋xnpn求出均值其中第1、2步是解答此类题目的关键．
跟踪训练2　在一场娱乐晚会上，有5名民间歌手(1至5号)登台演唱，由现场数百名观众投票选出最受欢迎歌手．各位观众必须独立地在选票上选3名歌手，其中观众甲是1号歌手的歌迷，他必选1号，不选2号，另在3至5号中随机选2名．观众乙和丙对5名歌手的演唱没有偏爱，因此在1至5号中随机选3名歌手．(1)求观众甲选3号歌手且观众乙未选3号歌手的概率；(2)X表示3号歌手得到观众甲、乙、丙的票数之和，求X的分布列及数学期望．
题型三　实际应用中的决策问题例3　某柑橘基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施．若实施方案一，预计当年可以使柑橘产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑橘产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二，预计当年可以使柑橘产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第二年可以使柑橘产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案时，第二年与第一年相互独立．记ξi(i＝1，2)表示方案i实施两年后柑橘产量达到灾前产量的倍数．(1)写出ξ1，ξ2的分布列； (2)实施哪种方案，两年后柑橘产量超过灾前产量的概率更大？(3)不管哪种方案，如果实施两年后柑橘产量达不到灾前产量，预计可带来效益10万元；两年后柑橘产量恰好达到灾前产量，预计可带来效益15万元；两年后柑橘产量超过灾前产量，预计可带来效益20万元．问：实施哪种方案所带来的平均效益更大？
解析：(1)ξ1所有可能的取值为0.8，0.9，1.0，1.125，1.25；ξ2所有可能的取值为0.8，0.96，1.0，1.2，1.44.ξ1，ξ2的分布列分别为
(2)令事件A、B分别表示方案一、方案二两年后柑橘产量超过灾前产量，由(1)可得，P(A)＝0.15＋0.15＝0.3，P(B)＝0.24＋0.08＝0.32.可见，方案二两年后柑橘产量超过灾前产量的概率更大．
(3)令ηi(i＝1，2)表示方案i所带来的效益，由题意及(1)易得η1，η2的分布列分别为
所以Eη1＝10×0.35＋15×0.35＋20×0.3＝14.75(万元)，Eη2＝10×0.5＋15×0.18＋20×0.32＝14.1(万元)．可见，方案一所带来的平均效益更大．
方法归纳解决实际问题的三个步骤(1)审题，确定实际问题是哪一种概率模型，可能用到的事件类型，所用的公式有哪些．(2)确定随机变量的分布列，计算随机变量的均值．(3)对照实际意义，回答概率、均值等所表示的结论．
(2)设小明、小红都选择方案甲所获得的累计得分为X1，都选择方案乙所获得的累计得分为X2，则X1，X2的分布列如下．
易错辨析　求均值时因求错分布列致误例4　一射手对靶射击，直到第一次命中为止，每次命中的概率为0.6，现有4颗子弹，则剩余子弹数目X的期望为________．
解析：X的可能取值为3，2，1，0.P(X＝3)＝0.6P(X＝2)＝0.4×0.6＝0.24P(X＝1)＝0.42×0.6＝0.096P(X＝0)＝0.43＝0.064所以EX＝3×0.6＋2×0.24＋1×0.096＋0×0.064＝2.376.
2．已知随机变量X的分布如表所示，则EX等于(　　)A.0 B．－0.2C．－1 D．－0.3
解析：由题可得0.5＋0.2＋p＝1，解得p＝0.3，则由离散型随机变量的均值公式得EX＝－1×0.5＋0×0.2＋0.3＝－0.2.
4．同学用身体语言把成语的意思传递给本组其他同学．若小组内同学甲猜对成语的概率是0.4，同学乙猜对成语的概率是0.5，且规定猜对得1分，猜不对得0分，则这两个同学各猜1次，得分之和X(单位：分)的数学期望为________．
解析：依题意得，得分之和X的可能取值分别是0，1，2，且P(X＝0)＝(1－0.4)(1－0.5)＝0.3，P(X＝1)＝0.4×(1－0.5)＋(1－0.4)×0.5＝0.5，P(X＝2)＝0.4×0.5＝0.2，所以得分之和X的分布列为
所以EX＝0×0.3＋1×0.5＋2×0.2＝0.9.
5．某研究机构准备举行一次数学新课程研讨会，共邀请50名一线教师参加，使用不同版本教材的教师人数如表所示：若随机选出2名使用人教版的教师发言，设使用人教A版的教师人数为X，求随机变量X的分布列和数学期望．