2024年中考数学压轴题之二次函数相似三角形存在性问题（二）（试题）

这是一份2024年中考数学压轴题之二次函数相似三角形存在性问题（二）（试题），共8页。试卷主要包含了如图1，已知抛物线的方程C1等内容，欢迎下载使用。

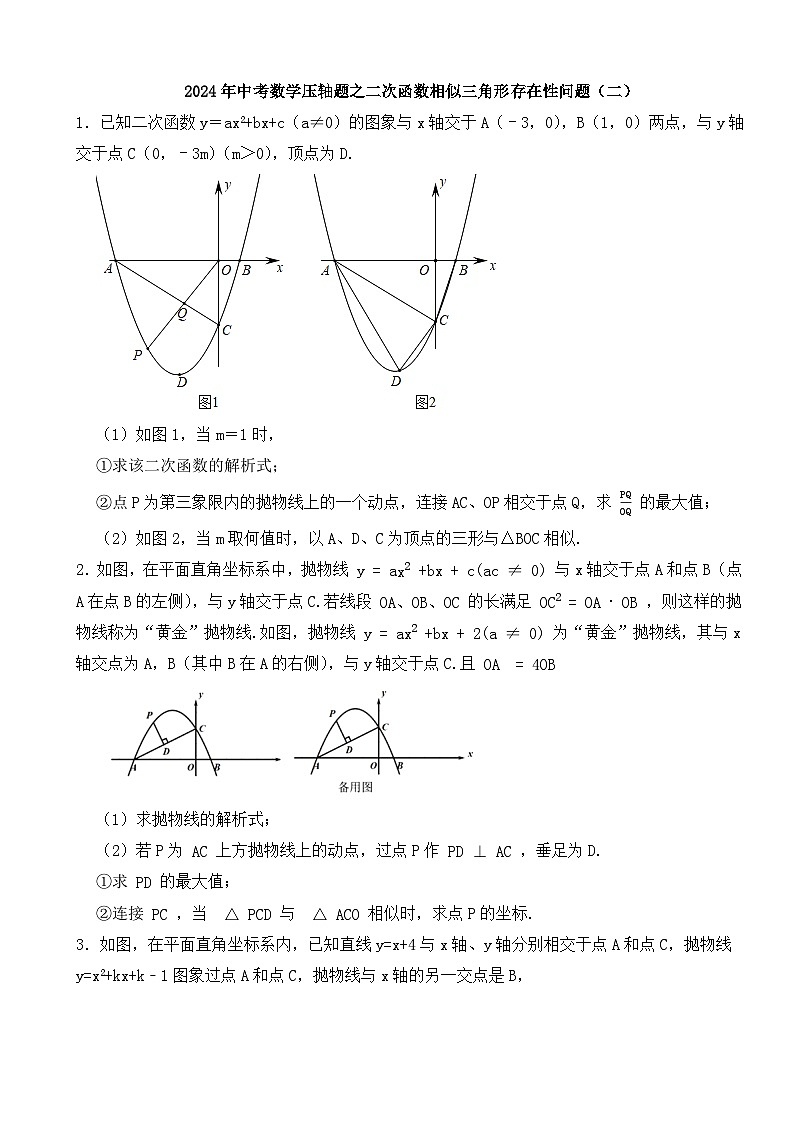
（1）如图1，当m＝1时，
①求该二次函数的解析式；
②点P为第三象限内的抛物线上的一个动点，连接AC、OP相交于点Q，求 PQOQ 的最大值；
（2）如图2，当m取何值时，以A、D、C为顶点的三形与△BOC相似.
2．如图，在平面直角坐标系中，抛物线 y=ax2+bx+c(ac≠0) 与x轴交于点A和点B（点A在点B的左侧），与y轴交于点C.若线段 OA、OB、OC 的长满足 OC2=OA⋅OB ，则这样的抛物线称为“黄金”抛物线.如图，抛物线 y=ax2+bx+2(a≠0) 为“黄金”抛物线，其与x轴交点为A，B（其中B在A的右侧），与y轴交于点C.且 OA=4OB
（1）求抛物线的解析式；
（2）若P为 AC 上方抛物线上的动点，过点P作 PD⊥AC ，垂足为D.
①求 PD 的最大值；
②连接 PC ，当 △PCD 与 △ACO 相似时，求点P的坐标.
3．如图，在平面直角坐标系内，已知直线y=x+4与x轴、y轴分别相交于点A和点C，抛物线y=x2+kx+k﹣1图象过点A和点C，抛物线与x轴的另一交点是B，
（1）求出此抛物线的解析式、对称轴以及B点坐标；
（2）若在y轴负半轴上存在点D，能使得以A、C、D为顶点的三角形与△ABC相似，请求出点D的坐标．
4．如图，二次函数y=﹣x2+ 53 x+4与x轴交于A、B两点，与y轴交于点C，点P从点O出发沿OA以每秒1个单位长度的速度向点A运动，到达点A后立刻在以原来的速度沿AO返回；点Q从点A出发沿AC以每秒1个单位长度的速度向点C匀速运动，过点Q作QD⊥x轴，垂足为D．点P、Q同时出发，当点Q到达点C时停止运动，点P也随之停止．设点P，Q的运动时间为t（t≥0）．
（1）当点P从点O向点A运动的过程中，求△QPA面积S与t的函数关系式；
（2）当线段PQ与抛物线的对称轴没有公共点时，请直接写出t的取值范围；
（3）当t为何值时，以P、D、Q为顶点的三角形与△OBC相似；
（4）如图2：FE保持垂直平分PQ，且交PQ于点F，交折线QC﹣CO﹣OP于点E，在整个运动过程中，请你直接写出点E所经过的路径长．
5．如图，已知抛物线y= 13 x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．
（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．
6．如图1，已知抛物线的方程C1： y=−1m(x+2)(x−m) (m＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．
（1）若抛物线C1过点M(2， 2)，求实数m的值；
（2）在（1）的条件下，求△BCE的面积；
（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH＋EH最小，求出点H的坐标；
（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．
7．如图所示，抛物线y=x2+bx+c经过A、B两点，A、B两点的坐标分别为（﹣1，0）、（0，﹣3）．
（1）求抛物线的函数解析式；
（2）点E为抛物线的顶点，点C为抛物线与x轴的另一交点，点D为y轴上一点，且DC=DE，求出点D的坐标；
（3）在第二问的条件下，在直线DE上存在点P，使得以C、D、P为顶点的三角形与△DOC相似，请你直接写出所有满足条件的点P的坐标．
8．如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点A的坐标为（﹣1，0），且OC=OB，tan∠ACO= 14 ．
（1）求抛物线的解析式；
（2）若点D和点C关于抛物线的对称轴对称，直线AD下方的抛物线上有一点P，过点P作PH⊥AD于点H，作PM平行于y轴交直线AD于点M，交x轴于点E，求△PHM的周长的最大值；
（3）在（2）的条件下，以点E为端点，在直线EP的右侧作一条射线与抛物线交于点N，使得∠NEP为锐角，在线段EB上是否存在点G，使得以E，N，G为顶点的三角形与△AOC相似？如果存在，请求出点G的坐标；如果不存在，请说明理由．
9．如图，二次函数y=x2-2mx+8m的图象与x轴交于A、B两点（点A在点B的左边且OA≠OB)，交y轴于点C，且经过点（m，9m），⊙E过A、B、C三点。
（1）求这条抛物线的解析式；
（2）求点E的坐标；
（3）过抛物线上一点P（点P不与B、C重合）作PQ⊥x轴于点Q，是否存在这样的点P使△PBQ和△BOC相似？如果存在，求出点P的坐标；如果不存在，说明理由
10．如图，抛物线 y=ax2+bx−2 与x轴交于A、B两点，与y轴交于点C，已知A（–1，0），且直线BC的解析式为y= 12 x-2，作垂直于x轴的直线 x=m ，与抛物线交于点F，与线段BC交于点E（不与点B和点C重合）.
（1）求抛物线的解析式；
（2）若△CEF是以CE为腰的等腰三角形，求m的值；
（3）点P为y轴左侧抛物线上的一点，过点P作 PM⊥BC 交直线BC于点M，连接PB，若以P、M、B为顶点的三角形与△ABC相似，求P点的坐标.
11．如图，已知抛物线 y=ax2+bx+c 与 x 轴交于 A、B ，且点 A(1,0) ，与y轴交于点 C(0,−2) ，其对称轴为直线 x=52 ．
（1）求这条抛物线的解析式；
（2）若在x轴上方的抛物线上有点D，使 △BCD 的内心恰好在x轴上，求此时 △BCD 的面积；
（3）在直线 BC 上方的抛物线上有一动点P，过P作 PM⊥x 轴，垂足为M是否存在P点，使得以 B、P、M 为顶点的三角形与 △OAC 相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
12．如图，已知抛物线y=−x2+bx+c经过A(0，3)和B(72，−94)两点，直线AB与x轴相交于点C，P是直线AB上方的抛物线上的一个动点，PD⊥x轴交直线AB于点D．
（1）求该抛物线的表达式；
（2）若PE∥x轴交直线AB于点E，求PD+PE的最大值；
（3）若以A，P，D为顶点的三角形与△AOC相似，请求出所有满足条件的点P，点D的坐标．
13．如图，直线y=−23x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=−43x2+bx+c经过点A，B．
（1）求点B的坐标和抛物线的解析式；
（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．
①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标.
②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点“．请直接写出使得M，P，N三点成为“共谐点”的m的值．
14．如图，抛物线y＝﹣x2+bx+c交x轴于A，B两点，交y轴于点C，直线BC的表达式为y＝﹣x+3．
（1）求抛物线的表达式；
（2）动点D在直线BC上方的二次函数图象上，连接DC，DB，设△BCD的面积为S，求S的最大值；
（3）当点E为抛物线的顶点时，在x轴上是否存在一点Q，使得以A，C，Q为顶点的三角形与△BCE相似？若存在，请求出点Q的坐标．
15．如图，已知抛物线y＝ax2+bx+6经过两点A（﹣1，0），B（3，0），C是抛物线与y轴的交点.
（1）求抛物线的解析式；
（2）点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，设△PBC的面积为S，求S关于m的函数表达式（指出自变量m的取值范围）和S的最大值；
（3）点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N使得∠CMN＝90°，且△CMN与△OBC相似，如果存在，请求出点M和点N的坐标.
16． 已知抛物线y=ax2+bx+4(a>0)与x轴交于点A(1，0)和B(4，0)，与y轴交于点C．
（1）求抛物线的表达式；
（2）如图1，点P是线段BC上的一个动点(不与点B，C重合)，过点P作x轴的垂线交抛物线于点Q，联结OQ，当四边形OCPQ恰好是平行四边形时，求点Q的坐标；
（3）如图2，在(2)的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE=2∠ODQ，在直线QE上是否存在点F，使得△BEF与△ADC相似？若存在，求点F的坐标；若不存在，请说明理由．
17． 如图1，抛物线y=−x2+bx+c经过A(−1，0)，B(4，0)两点，与y轴相交于点C，连接BC，点P为线段BC上方抛物线上一动点（不含点B、C），过点P作x轴的垂线l，交BC于点G，交x轴于点E．
（1）求抛物线的表达式．
（2）过点C作CF⊥直线l，F为垂足，当点P运动到何处时，以P，C，F为顶点的三角形与△OBC相似？并求出此时点P的坐标．
（3）如图2，连接PC，PB，请问△PBC的面积S能否取得最大值？若能，请求出最大面积S，并求出此时点P的坐标；若不能，请说明理由．