广东省深圳市坪山区2023-2024学年八年级上学期期末数学试题（含解析）

这是一份广东省深圳市坪山区2023-2024学年八年级上学期期末数学试题（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八年级 数学
第一部分 选择题
一、选择题
1．下列各数中为无理数的是（ ）
A．B．C．D．
2．直角坐标系中，点在一次函数的图象上，则的值是（ ）
A．B．C．D．
3．下列条件中，可以判断是直角三角形的是（ ）
A．B．
C．，D．
4．如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差．根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（ ）
A．甲B．乙C．丙D．丁
5．如图所示的是一所学校的平面示意图，若用表示教学楼的位置，表示旗杆的位置，则实验楼的位置可表示成（ ）
A．B．C．D．
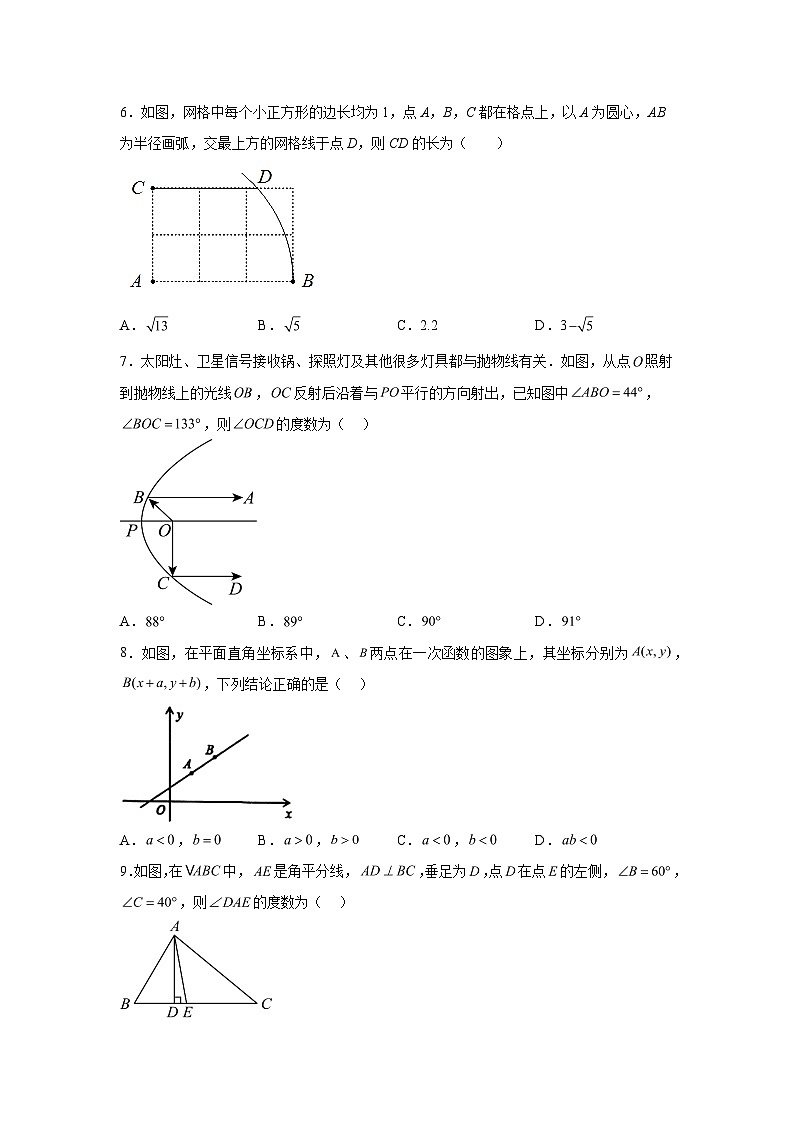
6．如图，网格中每个小正方形的边长均为1，点A，B，C都在格点上，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则CD的长为（ ）
A．B．C．2.2D．3
7．太阳灶、卫星信号接收锅、探照灯及其他很多灯具都与抛物线有关．如图，从点照射到抛物线上的光线，反射后沿着与平行的方向射出，已知图中，，则的度数为（ ）
A．B．C．D．
8．如图，在平面直角坐标系中，、两点在一次函数的图象上，其坐标分别为，，下列结论正确的是（ ）
A．，B．，C．，D．
9．如图，在中，是角平分线，，垂足为，点在点的左侧，，，则的度数为（ ）
A．B．C．D．
10．如图，平面直角坐标系中，点、的坐标分别为、，点在第一象限内，连接交轴于点，连接，，则的面积为（ ）
A．12B．20C．24D．25
第二部分 非选择题
二、填空题
11．比较大小： （填“”或“”）
12．若一次函数y＝3x﹣5与y＝2x﹣7的交点P坐标为（﹣2，﹣11），则方程组的解为 ．
13．某单位计划招聘一名管理人员、对甲、乙、丙三名候选人进行了笔试和面试两项测试．三人的测试成绩如表所示；根据录用程序，单位将笔试、面试两项测试得分按的比例确定个人成绩，成绩最高的将被录用，那么甲、乙、丙三人中被录用的候选人是 ．
14．2002年在北京石开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．如图，弦图是由四个能够重合的直角三角形与一个小正方形拼成的一个大正方形．若，，则小正方形的面积为 ．
15．如图，中，，于点，平分，交与点，于点，且交于点，若，，则 ．
三、解答题
16．化简：
(1)
(2)
17．解方程组：
18．教育部发布的《义务教育劳动课程标准（2022年版）》，将劳动从原来的综合实践活动课程中完全独立出来．某学校鼓励学生周末时间积极参加家务劳动，承担一定的家庭日常清洁、烹饪、家居美化等劳动，增强家庭责任意识．该校为了解八年级同学们周末家务劳动时间的大致情况，随机调查了部分八年级同学，并用得到的数据绘制了两幅统计图，请你根据图中信息，解答下列问题：
(1)一共调查了________人；并将条形统计图补充完整；
(2)本次抽查的学生周末劳动时间的众数是________小时，中位数为________小时；
(3)参与调查的学生甲说，“我周末参与家务劳动的时间是1.5小时，而调查中周末劳动1.5小时的学生人数最多，所以，我肯定达到了平均数．”你认为甲的说法对吗？请说明理由．
19．寒假快来了，小飞同学打算买一只200元的羽毛球拍．但是，他不想用爸妈的钱，打算利用春节前的消费热情，自己赚取．他瞄准小朋友节前买玩具的需求，用300元从批发市场购进甲、乙两种玩具，共40件．其中甲玩具的进价是9元/件，乙玩具的进价是7元/件．
(1)小飞购进甲、乙两种玩具各多少件？
(2)小飞计划将甲玩具15元/件卖出，乙玩具10元/件卖出，若甲、乙两种玩具都顺利卖完，小飞赚的钱够买那只羽毛球拍吗？
20．小明发现年级同学日常有买水喝的习惯，他调查得知，年级平均每人每天买水支出1.2元．假设年级人数是人．
(1)若学生自由买水喝，年级学生平均每天的总花费用表示，则与的函数关系是________；
(2)小明把发现的问题告知年级后，年级打算引入纯净水系统，调查得知，设备平均每天的固定维护费用是300元．实际使用过程中，学生人数与每天的总费用统计如下表：与之间的数量关系是一次函数吗？请你说明理由．
(3)该年级的人数为400人，引入纯净水系统划算吗？请你在右图中画出（1）（2）中的函数图象，然后结合图象给出结论．
21．如图，在平面直角坐标系中，，，过点作直线轴，点是直线上的动点，以为边在右上侧作等腰直角，使．
图1 图2 图3
(1)如图1当点落在点时，则点的坐标是________；
学生甲认为点的坐标一定跟点有关，于是进行了如下探究：
(2)如图2，小聪同学画草图时，让点落在、、不同的特殊位置时（在轴上、与轴平行、当落在轴上时对应点），画出了几个点对应的、、三个不同的位置，发现、、在同一条直线上，请你根据学生甲的猜测及题目条件，求出点所在直线的解析式；
(3)在（2）中，虽然求出了点所在直线的解析式，但是小明同学认为几个特殊点确定解析式是一种猜测，当点在上运动时，所有的点都在一条直线上吗？就解设了点的坐标为，希望用一般推理的方式求出和满足的关系式，请你帮助小明给出解答．
22．如下图，某学校计划在校内一道路旁建造超市，将地图简化，如图1所示，宿舍楼与校内道路的距离为50米，教学楼与校内道路的距离为160米，米，现要在校内道路旁建造一超市．
(1)请在图1中画出点（点在道路上，道路宽度忽略不记），使学生从宿舍楼走到超市，再走到教学楼所走路程最短，并求出最短路程．
(2)如图2所示，若宿舍楼和教学楼之间有一面70米长的校园文化墙，文化墙垂直于校内道路，到校内道路的距离为40米，米，米，现在依然要求学生从宿舍楼走到超市，再走到教学楼所走路程最短．
①众所周知，“两点之间，线段最短”，但由于文化墙这个障碍物的存在，需要研究两点之间不同折线长度的大小关系，他认为，并进行了证明，请你将下述证明过程补充完整：
证明：如图4，延长交于点，
，
又，________，
②如图5，延长交校内道路于点，过作于点，是上右侧的一点，利用①中证明的结论，可判断超市的位置应位于________（从以下四个选项中选择）．
A．左侧 B．线段上 C．线段上（不含点） D．右侧
③请在图6中画出超市的位置，并求出最短路程．
参考答案与解析
1．D
【分析】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，6，0.8080080008…（每两个8之间依次多1个0）等形式．依据定义即可作出判断．
【详解】A．是有理数，不符合题意；
B．是有理数，不符合题意；
C．是整数，不符合题意；
D．是无限不循环小数，是无理数，符合题意；
故选：D．
2．A
【分析】直接把点的坐标代入解析式得到a的一元一次方程，解方程即可.
【详解】∵点在一次函数的图象上，
∴3a+1=4
解得，a=1，
故选：A.
【点睛】本题主要考查一次函数图象上点的坐标特征，把点的坐标代入求解一元一次方程即可．
3．B
【分析】本题主要考查了勾股定理的逆定理，三角形内角和定理，若三角形中两较小边的平方和等于最长边的平方，那么这个三角形为直角三角形，有一个角为90度的三角形是直角三角形，据此求解即可．
【详解】解：A、任何三角形都满足，不能判断是直角三角形，不符合题意；
B、设，
∵，
∴是直角三角形，符合题意；
C、∵，，
∴，
∴不是直角三角形，不符合题意；
D、∵，，
∴，
∴不是直角三角形，不符合题意；
故选B．
4．A
【分析】此题考查了平均数和方差．首先比较平均数，平均数相同时选择方差较小的参加比赛．
【详解】解：∵甲和丙的平均数较大，
∴从甲和丙中选择一人参加竞赛，
∵甲的方差较小，
∴选择甲参加比赛，
故选：A．
5．B
【分析】本题主要考查了坐标确定位置．直接利用已知点坐标得出原点位置进而得出答案．
【详解】解：如图所示，
实验楼的位置可表示成．
故选∶B．
6．B
【分析】连接AD，由勾股定理即可得出CD的长．
【详解】解：如图，连接AD，则AD=AB=3，
由勾股定理可得，Rt△ADC中，
故选B．
【点睛】本题考查了勾股定理的运用，由连接AD构造直角三角形是解决问题的关键．
7．B
【分析】本题考查了平行线的性质，两直线平行，内错角相等．由平行线的性质即可得出，求得，再根据平行线的性质即可求解．
【详解】解：由题意知，
∴，
∴，
∴，
故选：B．
8．B
【分析】本题主要考查了点的坐标以及一次函数的性质．依据点A与点B的位置，即可得到点B的横坐标以及纵坐标都比点A的横坐标以及纵坐标大．
【详解】解：由题意可得，函数图象y随x增大而增大，
∴，
∴，，
故选：B．
9．A
【分析】本题主要考查三角形内角和定理、角平分线的定义以及三角形外角的性质．由，得由角平分线的定义，得．根据三角形外角的性质，得．由，根据三角形内角和定理，故可求得．
【详解】解：∵，
∴．
又∵是的角平分线，
∴，
∴．
∵，
∴，
∴．
故选：A．
10．C
【分析】本题主要考查了全等三角形的判定和性质，坐标与图形．过点B作轴于点E，则，证明，可得，再由，可得，可证明，可得，再根据的面积，即可求解．
【详解】解：如图，过点B作轴于点E，则，
∵点、的坐标分别为、，点，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
∴，
∴的面积
．
故选：C
11．
【分析】本题考查了实数的大小比较，根据实数的性质，运用比差法计算是解题的关键．
【详解】解：∵，
∴，
故答案为：．
12．
【分析】根据函数图象交点坐标为两函数解析式组成的方程组的解即可求解．
【详解】解：∵一次函数y＝3x﹣5与y＝2x﹣7的交点P坐标为（﹣2，﹣11），
∴方程组的解为．
故答案为：
【点睛】本题考查了一次函数与二元一次方程（组）的关系，函数图象交点坐标为两函数解析式组成的方程组的解．
13．甲
【分析】本题主要考查了加权平均数．根据加权平均数的概念分别计算出三人的得分，从而得出答案．
【详解】解：甲的最后成绩为：(分)，
乙的最后成绩为：(分)，
丙的最后成绩为：(分)，
，
最终被录用的是甲，
故答案为：甲．
14．4
【分析】本题考查了勾股定理．利用勾股定理求得的长，再利用小正方形面积计算即可求解．
【详解】解：在，，，，
∴，
∴小正方形面积，
故答案为：4．
15．##
【分析】本题考查了全等三角形的判定和性质，勾股定理，等腰三角形的性质．连接，证明，可得，从而得到，再由勾股定理求出，然后根据，可得，再由勾股定理，即可求出．
【详解】解：如图，连接，
∵，，
∴，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
∵平分，
∴，
在和中，
∵，，，
∴，
∴，
∵，
∴，
∴，
∵，
即，
解得：，
∴．
故答案为：
16．(1)
(2)5
【分析】此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．
（1）先利用二次根式的性质分别化简，再计算加减即可求解；
（2）先利用平方差公式将括号展开，再计算除法，进一步计算即可求解．
【详解】（1）解：
；
（2）解：
．
17．
【分析】本题主要考查了解二元一次方程组．利用加减消元法解答，即可求解．
【详解】解：
由，得：，
解得：，
把代入，得：，
解得：，
所以原方程组的解为．
18．(1)100，图见解析
(2)1.5；2
(3)甲的说法不正确．
【分析】（1）由图形中家庭劳动时间为2.5小时的人数及其所占百分比可得总人数，用总人数减去其它人数可得家庭劳动时间为1.5小时的人数，再将图形补充完整即可；
（2）根据众数和中位数的定义求解即可；
（3）根据平均数的定义计算即可判断．
【详解】（1）解：（人），
∴家庭劳动时间为1.5小时的人数为（人），
补全统计图如图所示：
；
故答案为：100；
（2）解：本次抽查的学生周末劳动时间最多的是1.5小时，则众数是1.5小时，
处于中间的两个数是2、2小时，则中位数为2小时；
故答案为：1.5；2；
（3）解：平均数为小时；
，
所以甲的说法不正确．
【点睛】本题考查条形统计图、扇形统计图、中位数、众数和平均数，掌握两个统计图中数量之间的关系，理解中位数的意义是解题的前提．
19．(1)购进甲种玩具10件，乙种玩具30件；
(2)甲、乙两种玩具都顺利卖完，小飞赚的钱不够买那只羽毛球拍．
【分析】本题考查了二元一次方程组的应用．
（1）设购进甲种玩具x件，乙种玩具y件，根据总价=单价×数量结合该商场用300元购进甲、乙两种玩具共40件，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）根据总利润=每件玩具的利润×数量，即可求出结论．
【详解】（1）解：解：设甲、乙两种玩具分别为x件、y件，
则：，
解得：，
答：购进甲种玩具10件，乙种玩具30件；
（2）解：（元）；
，
答：甲、乙两种玩具都顺利卖完，小飞赚的钱不够买那只羽毛球拍．
20．(1)
(2)与之间的数量关系是一次函数关系；
(3)该年级的人数为400人，引入纯净水系统划算．
【分析】本题考查了一次函数及其应用问题．
（1）根据题意即可得出；
（2）首先判断与的函数关系式为一次函数，再利用待定系数法求解即可；
（3）描点、连线，画出相关函数的图象，根据图象回答即可．
【详解】（1）解：∵年级平均每人每天买水支出1.2元，
∴与的函数关系式为，
故答案为：；
（2）解：根据题意每增加100人，年级学生平均每天的总花费增加40元，
∴设与的函数关系式为，
∴，解得，
∴与的函数关系式为；
故答案为：；
（3）解：当时，；当时，；
描点、连线，画出和的图象如图，

观察图象，该年级的人数为400人，引入纯净水系统划算．
21．(1)
(2)点所在直线的解析式为；
(3)见解析
【分析】本题主要考查平面直角坐标系和全等三角形的结合，作出辅助线利用线段相等去求点的坐标和直线的解析式是解题的关键．
（1）作于点，证明，推出，，据此即可求解；
（2）求得点的坐标是，由（1）知点的坐标是，利用待定系数法即可求解；
（3）作于，于，证明，利用全等三角形的性质即可求解．
【详解】（1）解：作于点，
∵，，
∴，，
∵，，
∴，
∴，
∴，，
∴点的坐标是，
故答案为：；
（2）解：当点在于直线上时，如图，
，
∴点的坐标是，
由（1）知点的坐标是，
设点所在直线的解析式为，
则，解得，
∴点所在直线的解析式为；
（3）解：如图，作于，于，
∵，
∴四边形是矩形，
，，
∴，，
，
在和中，
，
，
，，
∵点的坐标为，
∴，，，，
∵，
∴，
整理得．
22．(1)画图见解析，最短路程为
(2)①；②B；③画图见解析，最短路程为300米
【分析】此题考查了轴对称−最短路径问题，勾股定理，三角形三边的关系等知识，解题的关键是正确画出图形．
（1）作点A关于l的对称点，然后连接交l于点P，即为所求，得到的长度即为的最小值，过点A作交的延长线于点C，求出，，然后利用勾股定理求解即可；
（2）①根据三角形两边之和大于第三边求解即可；
②作点A关于l的对称点，然后根据①中证明的结论求解即可；
③首先根据题意画出图形，然后表示出相应线段的长度，然后利用勾股定理求解即可．
【详解】（1）如图所示，
∴，
∴的长度即为的最小值，
∵，，，
∴，，
∴，
∴；
（2）①证明：如图4，延长交于点，
，，
，
又，，
，
；
②如图所示，作点A关于l的对称点，
∴，，
由①中证明的结论可得，
，
∴超市的位置应位于线段上，
故选：B；
③如图所示，过点A作，过点B作，作点A关于l的对称点，连接交l于点P，过点作交延长线于点E，过点D作，
∵，，，
∴，，
∴，
∴，
∵，，
∴，，
∴，
∴，
∴．
∴最短路程为300米．
甲
乙
丙
丁
平均（）
方差
测试项目
测试成绩/分
甲
乙
丙
笔试
70
80
90
面试
90
80
70
/人
100
200
300
……
/元
340
380
420
……