山东省滨州市无棣县2024届九年级上学期期中学业水平检测数学试卷(含答案)

这是一份山东省滨州市无棣县2024届九年级上学期期中学业水平检测数学试卷(含答案)，共15页。

九年级数学试题
第Ⅰ卷 （选择题 共30分）
选择题（本题共10个小题，在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,每小题3分,满分30分）
1．随着我国航天领域的快速发展，从“天宫一号”发射升空，到天和核心舱归位，我国正式迈入了“空间站时代”．下面是有关我国航天领域的图标，其图标既是轴对称图形又是中心对称图形的是（ ）
A． B．C． D．
2．用配方法解方程x2﹣6x+4＝0时，配方后得的方程为（ ）
A．（x+3）2＝5B．（x﹣3）2＝﹣13
C．（x﹣3）2＝5D．（x﹣3）2＝13
3．抛物线y＝3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是（ ）
A．y＝3（x﹣1）2﹣2B．y＝3（x+1）2﹣2
C．y＝3（x+1）2+2D．y＝3（x﹣1）2+2
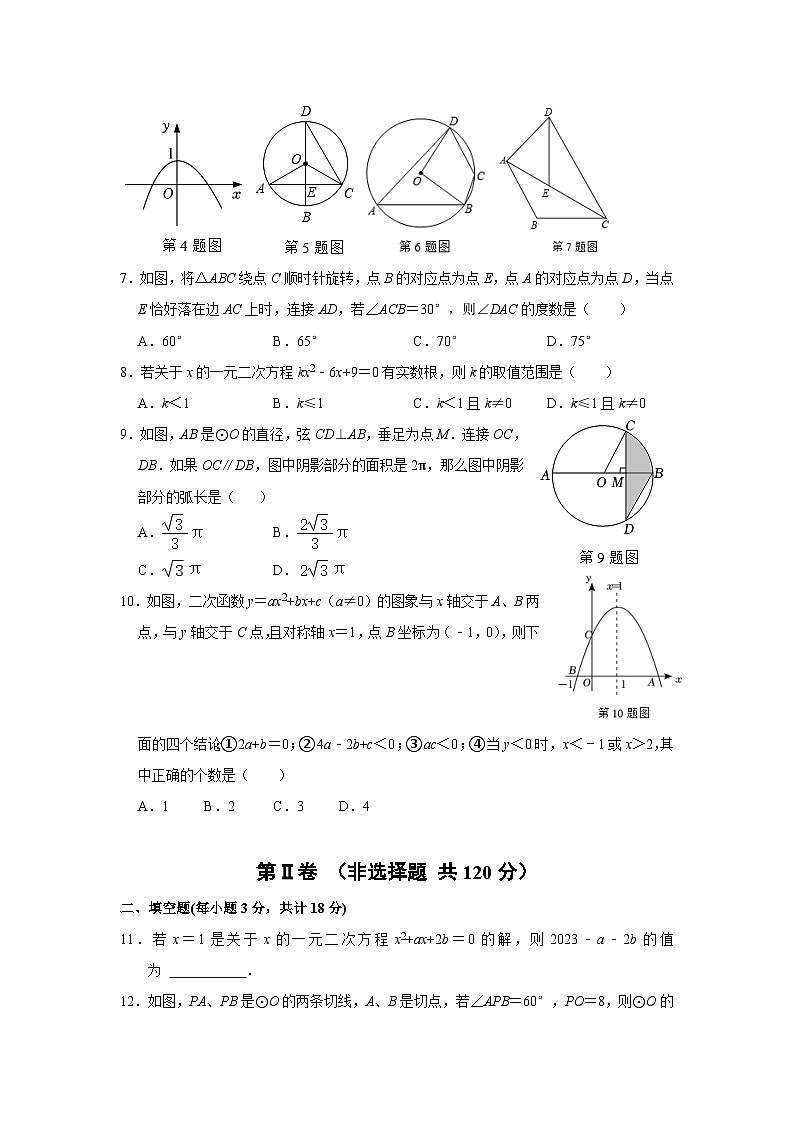
4．已知，二次函数y＝ax2+bx+c（a≠0）的图象如图，图象最高点落在y轴上，下列对b的取值正确的是（ ）
A．b＞0B．b＜0C．b＝0D．b＝1
5．如图，已知BD是⊙O的直径，BD⊥AC于点E，∠AOC＝100°，则∠BDC的度数是（ ）
A．20°B．25°C．30°D．40°
6．如图，四边形ABCD内接于⊙O，若∠C＝130°，则∠BOD的度数为（ ）
A．50°B．100°C．130°D．150°
7．如图，将△ABC绕点C顺时针旋转，点B的对应点为点E，点A的对应点为点D，当点E恰好落在边AC上时，连接AD，若∠ACB＝30°，则∠DAC的度数是（ ）
A．60°B．65°C．70°D．75°
8．若关于x的一元二次方程kx2﹣6x+9＝0有实数根，则k的取值范围是（ ）
A．k＜1B．k≤1C．k＜1且k≠0D．k≤1且k≠0
9．如图，AB是⊙O的直径，弦CD⊥AB，垂足为点M．连接OC，DB．如果OC∥DB，图中阴影部分的面积是2π，那么图中阴影部分的弧长是（ ）
A．B．
C．D．
10．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，且对称轴x＝1，点B坐标为（﹣1，0），则下面的四个结论：①2a+b＝0；②4a﹣2b+c＜0；③ac＜0；④当y＜0时，x＜﹣1或x＞2，其中正确的个数是（ ）
A．1 B．2C．3 D．4
第Ⅱ卷 （非选择题 共120分）
二、填空题(每小题3分，共计18分)
11．若x＝1是关于x的一元二次方程x2+ax+2b＝0的解，则2023﹣a﹣2b的值为 ．
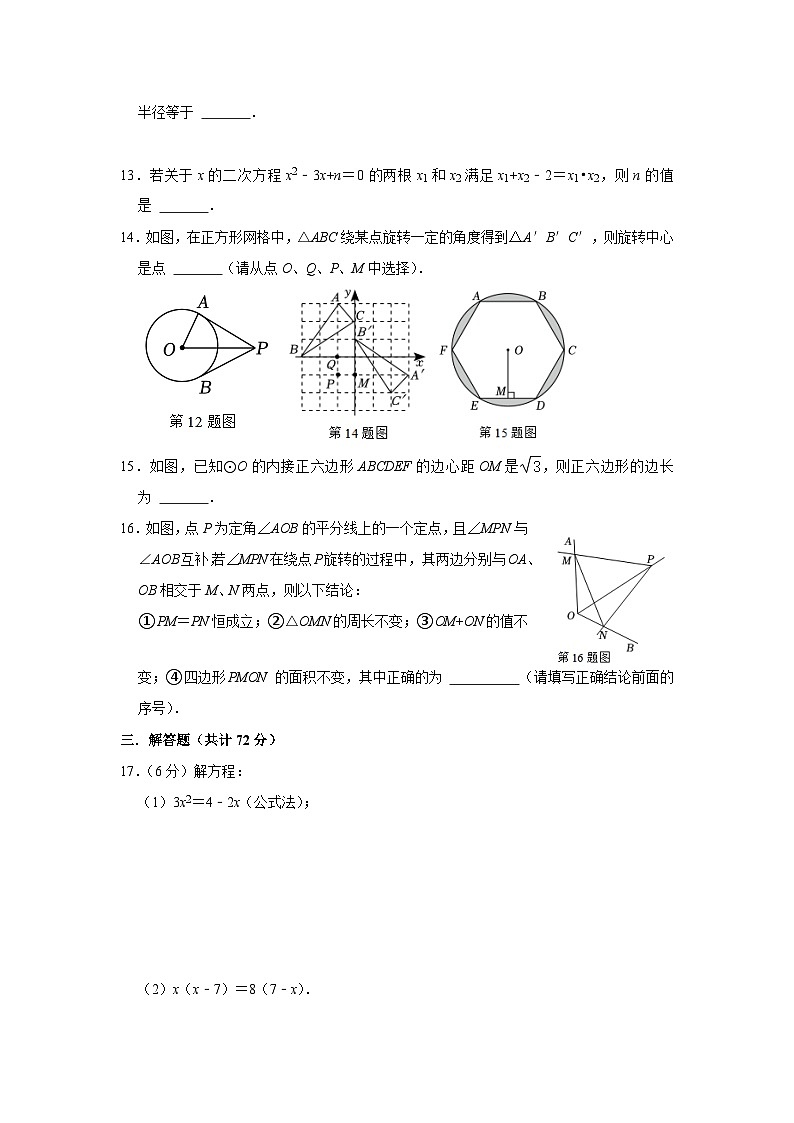
12．如图，PA、PB是⊙O的两条切线，A、B是切点，若∠APB＝60°，PO＝8，则⊙O的半径等于 ．
13．若关于x的二次方程x2﹣3x+n＝0的两根x1和x2满足x1+x2﹣2＝x1•x2，则n的值是 ．
14．如图，在正方形网格中，△ABC绕某点旋转一定的角度得到△A′B′C′，则旋转中心是点 （请从点O、Q、P、M中选择）．
15．如图，已知⊙O的内接正六边形ABCDEF的边心距OM是，则正六边形的边长为 ．
16．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：
①PM＝PN恒成立；②△OMN的周长不变；③OM+ON的值不变；④四边形PMON的面积不变，其中正确的为 （请填写正确结论前面的序号）．
三．解答题（共计72分）
17．（6分）解方程：
（1）3x2＝4﹣2x（公式法）；
（2）x（x﹣7）＝8（7﹣x）．
18．（6分）如图，在平面直角坐标系中，A（﹣1，4），B（﹣4，0），C（﹣1，0）．
（1）△A1B1C1与△ABC关于原点O对称，写出点A1、B1、C1的坐标；
（2）△A2B2C2是△ABC绕原点O顺时针旋转90°得到的，写出A2、B2、C2的坐标．
19．（6分）如图，△ABC内接于⊙O，动手操作．
（1）求作：三角形ABC的内切圆I；要求：尺规作图，不写作法，但保留作图痕迹．推理发现；
（2）若AI与⊙O交于点D，连接BD，DC．求证：BD＝DI＝DC．
20．（8分）如图，⊙O的直径AB＝10cm，弦AC＝6cm，∠ACB的平分线交⊙O于D．
（1）判断△ABD的形状，并说明理由；
（2）求点O到弦BD的距离．
21．（8分）如图，利用一面墙（墙长25米），用总长度49米的栅栏（图中实线部分）围成一个矩形围栏ABCD，且中间共留两个1米的小门，设栅栏BC长为x米．
（1）AB＝ 米（用含x的代数式表示）；
（2）若矩形围栏ABCD面积为210平方米，求栅栏BC的长；
（3）矩形围栏ABCD面积是否有可能达到240平方米？若有可能，求出相应x的值，若不可能，请说明理由．
22．（8分）如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，直线BF与AD延长线交于点F，且∠AFB＝∠ABC．
（1）求证：直线BF是⊙O的切线；
（2）若CD＝12，BE＝3，求⊙O的半径．
23．（10分）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣4与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C，点D为BC的中点．
（1）求该抛物线的函数表达式；
（2）点G是该抛物线对称轴上的动点，若GA+GC有最小值，求此时点G的坐标；
（3）若点P是第四象限内该抛物线上一动点，求△BDP面积的最大值．
24．（8分）如图，排球运动场的场地长18m，球网高度2.24m，球网在场地中央，距离球场左、右边界均为9m．一名球员在场地左侧边界练习发球，排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分．
在球运行时，将球与场地左边界的水平距离记为x（米），与地面的高度记为y（米），经多次测试后，得到如下数据：
（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；
（2）击球点的高度为 米，排球飞行过程中可达到的最大高度为 米；
（3）求出y与x的函数解析式；
（4）判断排球能否过球网，并说明理由．
25．（12分）阅读下面材料，并解决问题：
（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB＝ ；
（2）基本运用
请你利用第（1）题的解答思想方法，解答下面问题
已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF2＝BE2+FC2；
（3）能力提升
如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．
2023—2024学年义务教育第一次学业质量监测纸笔测试
九年级数学试题参考答案
11．2024 12．4 13．1 14．P 15. 2 16．①③④
三．解答题（共9小题，满分72分）
17．（1）3x2＝4﹣2x，
移项，得3x2+2x﹣4＝0，
这里a＝3，b＝2，c＝﹣4，
b2﹣4ac＝4+48＝52．
∴x＝
＝
＝．
∴x1＝，x2＝．………………3分
（2）x（x﹣7）＝8（7﹣x），
移项，得x（x﹣7）+8（x﹣7）＝0，
∴（x﹣7）（x+8）＝0．
∴x1＝7，x2＝﹣8．………………6分
18．解：（1）如图，△A1B1C1即为所求，A1（1，﹣4），B1（4，0），C1（1，0）；…3分
（2）如图，△A2B2C2即为所求，A2（4，1），B2（0，4），C2（0，1）．………………6分
19．解（1）如图所示，
………………………………3分
⊙I就是所求作的△ABC的内切圆；
（2）证明：∵⊙I就是所求作的△ABC的内切圆，
∴
∴BD＝DC，
∵∠DIB＝∠ABI+∠BAI，
∠DBI＝∠DBC+∠IBC，
又∠ABI＝∠CBI，
∠DBC＝∠DAC＝∠BAI，
∴∠DBI＝∠DIB，
∴BD＝DI．
∴BD＝DI＝DC．…………………………………………6分
20．解：（1）△ABD是等腰直角三角形，理由如下：
∵AB是⊙O的直径，
∴∠ACB＝∠ADB＝90°，
∵∠ACB的平分线交⊙O于D，
∴∠ACD＝∠BCD＝45°，
∴，
∴AD＝BD，
∴△ABD是等腰直角三角形；…………………………4分
（2）过O作OE⊥DB于E，如图所示：
则∠OEB＝90°，
∵AB＝10cm，
∴OB＝AB＝5（cm），
由（1）得：△ABD是等腰直角三角形，
∴∠ABD＝45°，
∴△OBE是等腰直角三角形，
∴OE＝OB＝（cm），
即点O到弦BD的距离为cm；………………………………8分
21．解：（1）设栅栏BC长为x米，
∵栅栏的全长为49米，且中间共留两个1米的小门，
∴AB＝49+2﹣3x＝51﹣3x（米），
故答案为：（51﹣3x）；……………………………………2分
（2）依题意，得：（51﹣3x）x＝210，
整理，得：x2﹣17x+70＝0，
解得：x1＝7，x2＝10．
当x＝7时，AB＝51﹣3x＝30＞25，不合题意，舍去，
当x＝10时，AB＝51﹣3x＝21，符合题意，
答：栅栏BC的长为10米；………………………………5分
（3）不可能，理由如下：
依题意，得：（51﹣3x）x＝240，
整理得：x2﹣17x+80＝0，
∵Δ＝（﹣17）2﹣4×1×80＝﹣31＜0，
∴方程没有实数根，
∴矩形围栏ABCD面积不可能达到240平方米．…………8分
22．（1）证明：∵，
∴∠ABC＝∠ADC，
∵∠AFB＝∠ABC，
∴∠ADC＝∠AFB，
∴CD∥BF，
∵CD⊥AB，
∴AB⊥BF，
∵OB为⊙O的半径．
∴直线BF是⊙O的切线；……………………4分
（2）解：设⊙O的半径为R，连接OD，如图，
∵AB⊥CD，CD＝12，
∴，
∵BE＝3，
∴OE＝R﹣3，
在Rt△OED中，
∵OE2+DE2＝OD2，
∴R2＝（R﹣3）2+62，
解得：．
即⊙O的半径为．………………………………8分
23．解：（1）∵抛物线y＝ax2+bx﹣4与x轴交于点A（﹣2，0），B（4，0），
∴，
解得：，
∴该抛物线的函数表达式为；………………………3分
（2）解：点G是该抛物线对称轴上的动点，
∴GA＝GB，
∴GA+GC＝GB+GC，
∴当点G在直线BC与抛物线对称轴的交点上时，GA+GC最小，
令x＝0得，y＝﹣4，
∴点C的坐标为（0，﹣4），
设直线BC的解析式为y＝kx﹣4（k≠0），
把B（4，0）代入得，0＝4k﹣4，
解得：k＝1，
∴直线BC的解析式为y＝x﹣4，
抛物线的对称轴为直线x＝＝1，
联立得：，
解得：，
∴此时点G的坐标为（1，﹣3）；………………………………7分
（3）如图，过点P作PQ⊥x轴交BC于点Q，
∵B（4，0），（0，﹣4），点D为BC的中点，
∴D（2，﹣2），
设P（0＜m＜4），则Q（m，m﹣4），
∴PQ＝m﹣4﹣＝，
∴
＝
＝
＝，
∵，0＜m＜4，
∴当m＝2时，S△BDP有最大值为2．……………………………………10分
24．解：（1）函数图象如图所示，
……2分
（2）由抛物线可得，击球点的高度为2米，排球飞行过程中可达到的最大高度为2.5米，
故答案为：2，2.5；……………………4分
（3）设解析式为y＝a（x﹣6）2+2.5，
把（0，2）代入y＝a（x﹣6）2+2.5，得2＝a（0﹣6）2+2.5，
所以a＝﹣，
所以解析式为y＝﹣（x﹣6）2+2.5＝﹣x2+x+2；…………6分
（4）排球能过球网，理由如下：
当x＝9时，y＝﹣×（9﹣6）2+2.5＝2.375＞2.24，
∴排球能过球网．……………………8分
25．解：（1）∵△ACP′≌△ABP，
∴AP′＝AP＝3、CP′＝BP＝4、∠AP′C＝∠APB，
由题意知旋转角∠PA P′＝60°，
∴△AP P′为等边三角形，
P P′＝AP＝3，∠A P′P＝60°，
易证△P P′C为直角三角形，且∠P P′C＝90°，
∴∠APB＝∠AP′C＝∠A P′P+∠P P′C＝60°+90°＝150°；
故答案为：150°；……………………………………2分
（2）如图2，把△ABE绕点A逆时针旋转90°得到△ACE′，
由旋转的性质得，AE′＝AE，CE′＝BE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，
∵∠EAF＝45°，
∴∠E′AF＝∠CAE′+∠CAF＝∠BAE+∠CAF＝∠BAC﹣∠EAF＝90°﹣45°＝45°，
∴∠EAF＝∠E′AF，
在△EAF和△E′AF中，
∴△EAF≌△E′AF（SAS），
∴E′F＝EF，
∵∠CAB＝90°，AB＝AC，
∴∠B＝∠ACB＝45°，
∴∠E′CF＝45°+45°＝90°，
由勾股定理得，E′F2＝CE′2+FC2，
即EF2＝BE2+FC2．……………………………………………………7分
（3）如图3，将△AOB绕点B顺时针旋转60°至△A′O′B处，连接OO′，
∵在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，
∴AB＝2，
∴BC＝，
∵△AOB绕点B顺时针方向旋转60°，
∴△A′O′B如图所示；
∠A′BC＝∠ABC+60°＝30°+60°＝90°，
∵∠C＝90°，AC＝1，∠ABC＝30°，
∴AB＝2AC＝2，
∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，
∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，
∴△BOO′是等边三角形，
∴BO＝OO′，∠BOO′＝∠BO′O＝60°，
∵∠AOC＝∠COB＝∠BOA＝120°，
∴∠COB+∠BOO′＝∠BO′A′+∠BOO′＝120°+60°＝180°，
∴C、O、A′、O′四点共线，
在Rt△A′BC中，A′C＝，
∴OA+OB+OC＝A′O′+OO′+OC＝A′C＝．………………………………12分
x（米）
0
1
2
4
6
7
8
y（米）
2
2.15
2.28
2.44
2.5
2.49
2.44
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
A
C
B
B
D
D
B
C