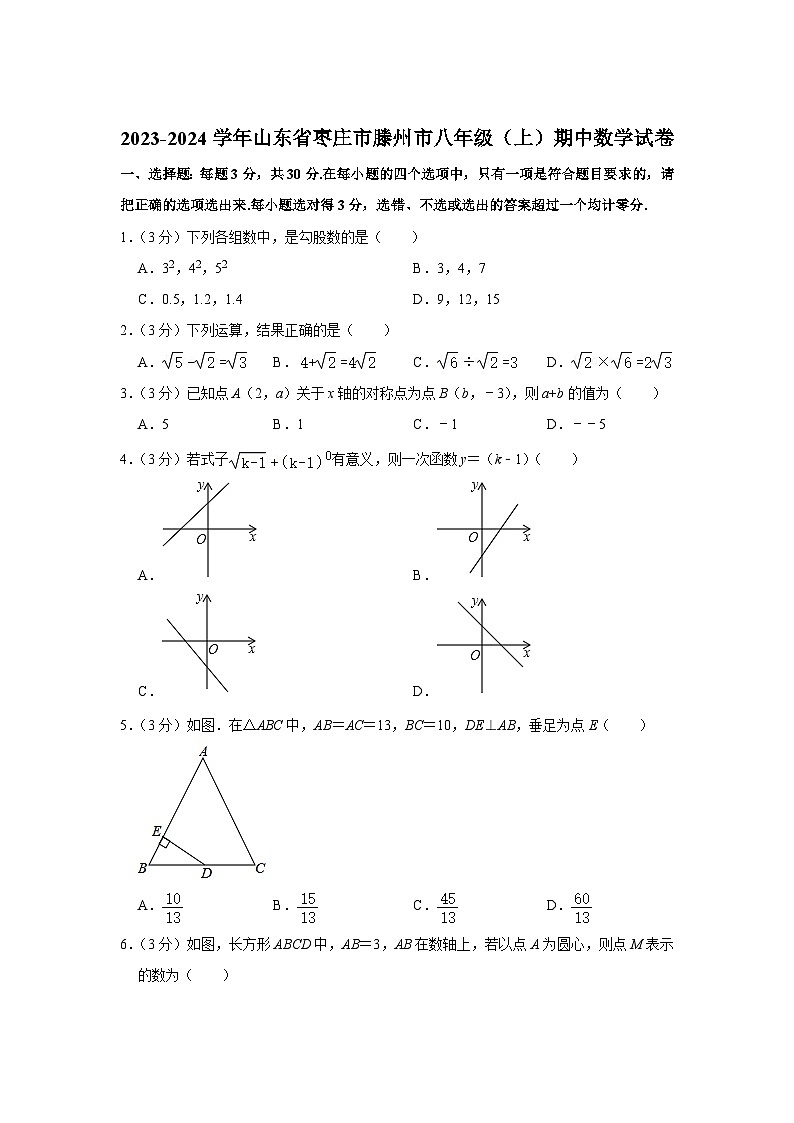
山东省枣庄市滕州市2023-2024学年八年级上学期期中考试数学试卷(含解析)

这是一份山东省枣庄市滕州市2023-2024学年八年级上学期期中考试数学试卷(含解析)，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：每题3分，共30分.在每小题的四个选项中，只有一项是符合题目要求的，请把正确的选项选出来.每小题选对得3分，选错、不选或选出的答案超过一个均计零分.
1．（3分）下列各组数中，是勾股数的是（ ）
A．32，42，52B．3，4，7
C．0.5，1.2，1.4D．9，12，15
2．（3分）下列运算，结果正确的是（ ）
A．B．C．D．
3．（3分）已知点A（2，a）关于x轴的对称点为点B（b，﹣3），则a+b的值为（ ）
A．5B．1C．﹣1D．﹣﹣5
4．（3分）若式子有意义，则一次函数y＝（k﹣1）（ ）
A．B．
C．D．
5．（3分）如图．在△ABC中，AB＝AC＝13，BC＝10，DE⊥AB，垂足为点E（ ）
A．B．C．D．
6．（3分）如图，长方形ABCD中，AB＝3，AB在数轴上，若以点A为圆心，则点M表示的数为（ ）
A．﹣1B．﹣1C．2D．
7．（3分）在等腰Rt△ABC中，点B，点C在直角坐标系中的坐标分别是（2，1），（﹣2，1）（ ）
A．（﹣2，5）B．（﹣2，﹣3）C．（0，﹣1）D．（2，3）
8．（3分）若函数y＝（m﹣1）x+m2﹣1是正比例函数，则m的值为（ ）
A．m＝﹣1B．m＝1C．m＝±1D．m≠1
9．（3分）若点P（a，b）在直线y＝2x+1上，则代数式1﹣4a+2b的值为（ ）
A．3B．﹣1C．2D．0
10．（3分）如图，直线y＝x+2与x轴、y轴分别交于点A和点B，点P为OA上一动点，PC+PD值最小时点P的坐标为（ ）
A．（﹣，0）B．（﹣，0）C．（﹣，0）D．（﹣，0）
二、填空题：每题3分，共18分，将答案填在题的横线上.
11．（3分）如图，正方形ABCD由四个全等的直角三角形和一个小正方形EFGH构成．设直角三角形的两条直角边分别为a，b（b＞a），正方形ABCD与正方形EFGH的面积分别为25，9 ．
12．（3分）计算：＝ ．
13．（3分）已知A（﹣2，1），B（﹣6，0），若白棋A飞挂后，黑棋C尖顶 ， ）．
14．（3分）若一次函数y＝﹣2x+1的图象过A（m，n），则4m+2n+2022的值为 ．
15．（3分）已知直线y＝x+3的图象与x，y轴交于A、B两点，直线l经过原点，把△AOB的面积分成2：1的两部分，则直线l的解析式为 ．
16．（3分）甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达B地并停留1h后，直至与甲车相遇．在此过程中，两车之间的距离y（km）（h）之间的函数关系如图所示．下列说法：①乙车的速度是120km/h；②m＝160（7，80）；④n＝7.4．其中说法正确的是 （填写序号）．
三、解答题：共8小题，满分72，解答应写出文字说明，说理过程或演算步骤.
17．（8分）计算：
（1）；
（2）×．
18．（8分）“某市道路交通管理条例”规定：小汽车在城市街路上行驶速度不得超过60千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，过了2秒后到达B处，测得小汽车与车速检测仪间距离为50米，则超速了多少？
19．（8分）如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A（3，4），B（5，﹣1），C（1，2）．
（1）作出与△ABC关于x轴对称的图形△A1B1C1；
（2）已知点P（﹣2a+3，a﹣1），直线PB1∥x轴，求点P的坐标．
20．（9分）先化简，再求值：a+，其中a＝1007．如图是小亮和小芳的解答过程．
（1） 的解法是错误的；
（2）错误的原因在于未能正确地运用二次根式的性质： ；
（3）先化简，再求值：，其中a＝﹣2023．
21．（10分）如图，一次函数的图象与x轴和y轴分别交于点A和B，使点A与点B重合、直线CD与x轴交于点C，与AB交于点D．
（1）点A的坐标为 ，点B的坐标为 ；
（2）求OC的长度；
（3）在直线AB上是否存在点P使得△APO的面积为20？若存在，请求出所有符合条件的点P的坐标；若不存在
22．（9分）如图，一次函数y＝﹣kx+1与x轴、y轴分别交于A、B两点，且∠BAO＝30°．
（1）如图1，把△AOB绕点A顺时针旋转60°后得到△AO′B′，则点B′的坐标是多少？
（2）如图2，把△AOB绕点A顺时针旋转90°后得到△AO″B″，则点B″的坐标是多少？
（3）如图3，若存在x轴上一点C，使△ACB为等腰三角形
23．（8分）我公司组织20辆货车到运A、B、C三种水果共100吨到外地销售，按计划：20辆车都要装运，每辆货车只能装运同一种水果，根据表提供的信息，解答以下问题：
（1）设安排x辆货车装运A水果，安排y辆货车装运B水果，求y与x之间的函数关系式；
（2）如果装运三种水果的车辆数都不少于2辆，怎样安排装运方案，使得三种水果全部售完所获得的利润最大？最大利润是多少？
24．（12分）如图，直线l是一次函数y＝kx+b的图象，直线经过点（3，﹣3），交y轴于点B（0，1）．
（1）求直线l的解析式；
（2）求l与两坐标轴所围成的三角形的面积；
（3）当x 时，y≥0；
（4）求原点到直线l的距离．
2023-2024学年山东省枣庄市滕州市八年级（上）期中数学答案
一、选择题：每题3分，共30分.在每小题的四个选项中，只有一项是符合题目要求的，请把正确的选项选出来.每小题选对得3分，选错、不选或选出的答案超过一个均计零分.
1．
解析：解：A、∵32＝7，42＝16，72＝25，95+162＜252，故选项错误，不符合题意；
B、∵42+42＜72，故选项错误，不符合题意；
C、∵6.5，1.2不符合勾股数定义，不符合题意；
D、∵92+125＝81+144＝225＝152，故选项正确，符合题意．
故选：D．
2．
解析：解：A． 与不能合并；
B．6与，所以B选项不符合题意；
C．原式＝＝；
D．原式＝＝，所以D选项符合题意．
故选：D．
3．
解析：解：∵点A（2，a）关于x轴的对称点是B（b，
∴a＝3，b＝2，
∴a+b＝3+2＝4．
故选：A．
4．
解析：解：∵式子有意义，
∴，解得k＞1，
∴k﹣4＞0，
∴一次函数y＝（k﹣1）x+k﹣2的图象过一、二、三象限．
故选：A．
5．
解析：解：连接AD，
∵△ABC中，AB＝AC＝13，D为BC中点，
∴AD⊥BC，BD＝，
∴AD＝＝12，
又∵DE⊥AB，
∴BD•AD＝，
∴ED＝＝＝，
故选：D．
6．
解析：解：由勾股定理，得
AC＝＝，
AM＝AC＝，
M点的坐标是﹣4，
故选：A．
7．
解析：解：如图，满足等腰Rt△ABC的A点坐标有（2、（0、（8、（2、（﹣2、（﹣5，
∴点A的坐标不可能是（2，3），
故选：D．
8．
解析：解：根据题意得，m2﹣1＝3且m﹣1≠0，
解得m＝±2且m≠1，
所以m＝﹣1．
故选：A．
9．
解析：解：∵点P（a，b）在直线y＝2x+1上，
∴b＝7a+1，即2a﹣b＝﹣2，
1﹣4a+8b
＝1﹣2（3a﹣b）
＝1﹣2×（﹣4）
＝1+2
＝6．
故选：A．
10．
解析：解：作点D关于x轴的对称点D′，连接CD′交x轴于点P，如图．
令y＝x+6中x＝0，
∴点B的坐标为（0，4）；
令y＝x+4中y＝0，则，解得：x＝﹣3，
∴点A的坐标为（﹣3，4）．
∵点C、D分别为线段AB，
∴点C（﹣，5），1）．
∵点D′和点D关于x轴对称，
∴点D′的坐标为（0，﹣6）．
设直线CD′的解析式为y＝kx+b，
∵直线CD′过点C（﹣，5），﹣1），
∴有，解得：，
∴直线CD′的解析式为y＝﹣x﹣1．
令y＝5，则0＝﹣，解得：x＝﹣，
∴点P的坐标为（﹣，0）．
故选：A．
二、填空题：每题3分，共18分，将答案填在题的横线上.
11．
解析：解：
解得，ab＝8，
∵（a+b）2＝a2+2ab+b7＝（a2+b2）+6ab
∴（a+b）2＝25+2×2＝41，
∵b＞a＞0，
∴a+b＝，
故答案为：．
12．
解析：解：原式＝（+）×（﹣﹣）
＝（3﹣2）×（﹣）
＝﹣．
故答案为：﹣．
13．
解析：解：∵A（﹣2，1），5），
∴建立如图所示的平面直角坐标系，
∴C（﹣1，1）．
故答案为：﹣2，1．
14．
解析：解：∵一次函数y＝﹣2x+1的图象过A（m，n），
∴﹣5m+1＝n，
∴2m+n＝8，
∴4m+2n+2022＝3（2m+n）+2022＝2×2+2022＝2024．
故答案为：2024．
15．
解析：解：由直线y＝x+3的解析式可求得A（﹣3，7），3），
如图（1），当直线l把△ABO的面积分为S△AOC：S△BOC＝2：6时，
作CF⊥OA于F，CE⊥OB于E，则△AOC＝2，
∴，即，
∴CF＝2，
∵＝，，
解得CE＝5．
∴C（﹣1，2），
∴直线l的解析式为y＝﹣2x；
如图（2），当直线l把△ABO的面积分为S△AOC：S△BOC＝1：2时，
同理求得C（﹣4，1），
∴直线l的解析式为．
16．
解析：解：由图象可知，乙出发时，2小时后．则说明乙每小时比甲快40km．①正确；
由图象第2﹣3小时，乙由相遇点到达B，每小时比甲快40km，则m＝160；
当乙在B休息1h时，甲前进80km，80）；
乙返回时，甲乙相距80km，则n＝6+4+0.4＝8.4，
故答案为：①②③④．
三、解答题：共8小题，满分72，解答应写出文字说明，说理过程或演算步骤.
17．
解析：解：（1）
＝12﹣（6）2﹣（3+3+2）
＝1﹣12﹣1﹣7﹣2
＝﹣15﹣6；
（2）×
＝﹣
＝﹣
＝1﹣．
18．
解析：解：根据题意，得AC＝30m，∠C＝90°，
在Rt△ACB中，根据勾股定理2＝AB2﹣AC3＝502﹣302＝408，
所以BC＝40，
小汽车2秒行驶40米，则1小时行驶20×3600＝72000（米），
即小汽车行驶速度为72千米/时，因为 72＞60．
19．
解析：解：（1）如图，△A1B1C3即为所求．
（2）∵B（5，﹣1）3与点B关于x轴对称，
∴B1（5，2）．
∵P（﹣2a+3，a﹣5）1∥x轴，
∴点P的纵坐标为1，
∴a﹣2＝1，
∴a＝2，
∴﹣2a+3＝﹣1，
∴点P的坐标为（﹣5，1）．
20．
解析：解：（1）小亮的解法是错误的，
故答案为：小亮；
（2）错误的原因在于未能正确地运用二次根式的性质＝﹣a（a＜0），
故答案为：＝﹣a（a＜0）；
（3）∵a＝﹣2007，
∴a﹣3＝﹣2010＜6，
则原式＝a+2
＝a+2|a﹣3|
＝a﹣2（a﹣3）
＝a﹣2a+8
＝﹣a+6
＝2023+6
＝2029．
21．
解析：解：（1）当x＝0时，y＝﹣，
∴点B的坐标为（0，4）；
当y＝8时，﹣x+6＝0，
解得：x＝8，
∴点A的坐标为（3，0）．
故答案为：（8，2），4）；
（2）设OC＝a，则AC＝8﹣a，
由折叠可知：BC＝AC＝5﹣a，
在Rt△BOC中，∠BOC＝90°，
∴BC2﹣OC2＝OB7，
∴（8﹣a）2﹣a4＝16，
∴a＝3，即OC＝3；
（3）存在，设点P的坐标为（m，﹣．
∵点A的坐标为（8，3），
∴AO＝8，
∴S△APO＝×AO×|yP|＝20，
∴×8×|﹣，
解得：m＝﹣6或m＝18，
当m＝﹣2时，﹣m+4＝﹣；
当m＝18时，﹣m+3＝﹣，
∴点P的坐标为（﹣4，5）或（18．
22．
解析：解：（1）∵一次函数y＝﹣kx+1与x轴、y轴分别交于A，
令x＝0，则y＝6，
∴点B（0，1），
∴OB＝3，
∵∠BAO＝30°．
∴AB＝2，OA＝，
∵旋转角是60°，
∴∠OAB′＝30°+60°＝90°，AB′＝AB＝4，
∴AB′⊥x轴，
∴点B′（，2）；
（2）∵把△AOB绕点A顺时针旋转90°后得到△AO″B″，
∴O″A＝OA＝，O″B″＝OB＝1，∠AO″B″＝∠AOB＝90°，
∴O″A⊥x轴，O″B″∥x轴，
∴B″点到x轴距离为，到y轴距离为，
∴点B″的坐标为（+1，）；
（3）如图，
①当AB＝BC时，
∵OB⊥x轴，
∴OA＝OC，
∴点C1的坐标为：（﹣，7）；
②当AB＝AC时，
∵AB＝2，
点C2（6+，0）7（﹣2；
③当AC＝BC时，
设点C8（x，0），
则﹣x＝，
解得：x＝，
∴点C3的坐标为：（，0）；
综上可得：点C的坐标为：（﹣，0）或（2+﹣2，0）．
23．
解析：解：（1）根据题意，装运C水果有20﹣x﹣y辆货车，
∴6x+5y+4（20﹣x﹣y）＝100，
∴y＝﹣2x+20．
（2）∵装运三种水果的车辆数都不少于2辆，
∴x≥2，﹣2x+20≥2，
∴8≤x≤9，
∴x＝2，4，4，5，7，7，8或3．
三种水果全部售完所获得的利润m＝500×6x+600×5y+400×4（20﹣x﹣y）＝﹣1400x+60000，
∴m＝﹣1400x+60000（x＝2，3，6，5，6，6，8或9）．
∵m随x的减小而增大，
∴当x＝2时，y＝﹣2×2+20＝16，m＝﹣1400×3+60000＝57200．
∴安排2辆货车装运A水果，安排16辆货车装运B水果，使得三种水果全部售完所获得的利润最大．
24．
解析：解：（1）把（3，﹣3），5）代入y＝kx+b，
得，
解得：，
∴直线l的解析式为y＝﹣x+8；
（2）在y＝﹣x+3中，则﹣，
解得x＝，
∴A（，0），
∵B（0，6），
∴OA＝，OB＝4，
∴S△AOB＝＝×1＝，
∴直线l与两坐标轴所围成的三角形的面积为；
（3）∵A（，0），
∴当x≤时，y≥0；
故答案为：≤；
（4）设原点到直线的距离为h，
∵OA＝，OB＝1，
∴AB＝＝＝，
∵S△AOB＝AB•h，
∴＝×h，
∴h＝．
故原点到直线l的距离为．
水果
A
B
C
每辆货车运载量吨
6
5
4
每吨水果获利元
500
600
400