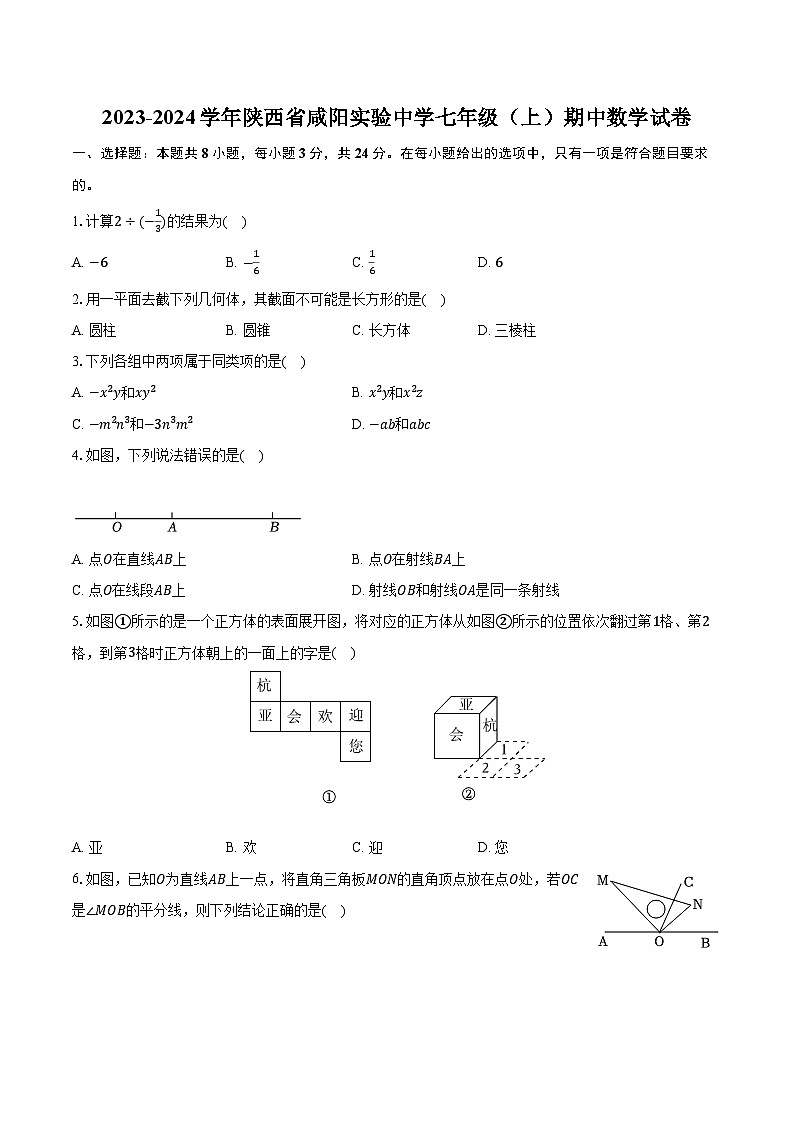
2023-2024学年陕西省咸阳实验中学七年级（上）期中数学试卷（含解析）

这是一份2023-2024学年陕西省咸阳实验中学七年级（上）期中数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.计算2÷(−13)的结果为( )
A. −6B. −16C. 16D. 6
2.用一平面去截下列几何体，其截面不可能是长方形的是( )
A. 圆柱B. 圆锥C. 长方体D. 三棱柱
3.下列各组中两项属于同类项的是( )
A. −x2y和xy2B. x2y和x2z
C. −m2n3和−3n3m2D. −ab和abc
4.如图，下列说法错误的是( )
A. 点O在直线AB上B. 点O在射线BA上
C. 点O在线段AB上D. 射线OB和射线OA是同一条射线
5.如图①所示的是一个正方体的表面展开图，将对应的正方体从如图②所示的位置依次翻过第1格、第2格，到第3格时正方体朝上的一面上的字是( )
A. 亚B. 欢C. 迎D. 您
6.如图，已知O为直线AB上一点，将直角三角板MON的直角顶点放在点O处，若OC是∠MOB的平分线，则下列结论正确的是( )
A. ∠AOM=3∠NOCB. ∠AOM=2∠NOC
C. 2∠AOM=3∠NOCD. 3∠AOM=5∠NOC
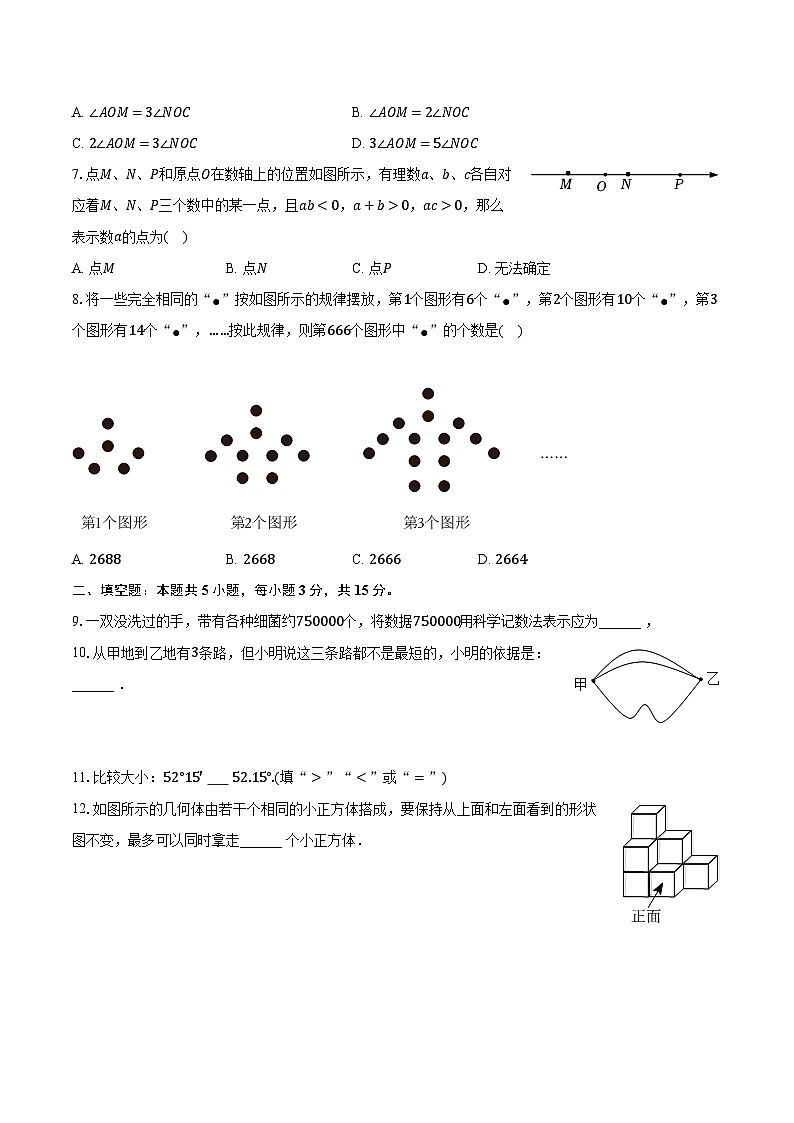
7.点M、N、P和原点O在数轴上的位置如图所示，有理数a、b、c各自对应着M、N、P三个数中的某一点，且ab<0，a+b>0，ac>0，那么表示数a的点为( )
A. 点MB. 点NC. 点PD. 无法确定
8.将一些完全相同的“●”按如图所示的规律摆放，第1个图形有6个“●”，第2个图形有10个“●”，第3个图形有14个“●”，……按此规律，则第666个图形中“●”的个数是( )
A. 2688B. 2668C. 2666D. 2664
二、填空题：本题共5小题，每小题3分，共15分。
9.一双没洗过的手，带有各种细菌约750000个，将数据750000用科学记数法表示应为______ ，
10.从甲地到乙地有3条路，但小明说这三条路都不是最短的，小明的依据是：______ ．
11.比较大小：52°15′ 52.15°.(填“>”“<”或“=”)
12.如图所示的几何体由若干个相同的小正方体搭成，要保持从上面和左面看到的形状图不变，最多可以同时拿走______ 个小正方体．
13.某工厂计划购买A、B两种型号的机器共33台，已知A、B两种型号机器的单价分别为2.6万元/台和1.5万元/台，若购买A型号机器的费用为2.6(15+x)万元(x<18)，则购买A、B两种型号的机器的总费用为______ 万元．
三、解答题：本题共13小题，共81分。解答应写出文字说明，证明过程或演算步骤。
14.(本小题5分)
计算：
(1)−6×|−13|÷(−2)−12；
(2)−32−[8÷(−2)3−1]+12÷2×12．
15.(本小题5分)
已知线段a，b，点A，P的位置如图所示，画射线AP，并用尺规作图法在射线AP上求作线段AB，使得AB=AP+b−a.(保留作图痕迹，不写作法)
16.(本小题5分)
小明利用星期天制作了一个底面边长都为4cm，侧棱长为16cm的五棱柱形的无盖笔筒．
(1)这个五棱柱笔筒的外部共有多少个面？多少条棱？
(2)制作这个笔筒的侧面至少需要多少平方厘米的材料？
17.(本小题5分)
阅读下列材料：
计算：124÷(13−14+112).
解法一：原式=124÷13−124÷14+124÷112=124×3−124×4+124×12=1124．
解法二：原式=124÷(412−312+112)=124÷212=124×6=14．
解法三：原式的倒数=(13−14+112)÷124=(13−14+112)×24=13×24−14×24+112×24=4．
所以，原式=14．
(1)上述得到的结果不同，你认为解法______是错误的；
(2)请你选择合适的解法计算：(−142)÷(16−314+23−27).
18.(本小题5分)
先化简，在求值：−13(6xy−9x)+34(−8x+4xy)+xy，其中x=−3，y=−2．
19.(本小题5分)
已知正多边形的周长为56，从其一个顶点出发共有4条对角线，求这个正多边形的边长．
20.(本小题5分)
有20袋大米，以每袋30千克为标准，超过或不足的千克数分别用正负数来表述，记录如下：
(1)20袋大米中，最重的一袋比最轻的一袋重多少千克？
(2)与标准重量比较，20袋大米总计超过(或不足)多少千克？
(3)若大米每千克售价为10元，出售这20袋大米可卖多少元？
21.(本小题6分)
已知多项式：A=4x2−4xy+y2，3A−B=13x2−11xy−2y2．
(1)求多项式B；
(2)若x是单项式−6m2n的系数，y是−12的倒数，求B的值．
22.(本小题7分)
如图，C为线段AB的中点，点D在线段AB上，且AD：BD=3：2，若E为线段DB的中点，请判断线段AD，线段CE的数量关系，并说明理由．
23.(本小题7分)
如图，长为y cm，宽为x cm的大长方形被分㸝成7块，除阴影部分的A和B外，其他5块空白部分是形状、大小完全相同的小长方形，且小长方形的宽为5cm．
(1)由图可知：每个小长方形的长为______ cm；(用含x或y的代数式表示)
(2)用含x或y的代数式表示阴影部分A和B的周长之和；(结果化为最简形式)
(3)当y=30时，用含x的代数式表示阴影部分A与B的面积之和．
24.(本小题8分)
如图所示，OB是∠AOC的平分线，OD是∠COE的平分线．
(1)如果∠AOB=40°，∠DOE=25°，求∠BOE的度数；
(2)如果∠AOE=120°，∠COD=20°，求∠AOB的度数．
25.(本小题8分)
阅读理解：蕊蕊是一个勤奋好学的学生，她常常通过书籍、网络等渠道主动学习各种知识，下面是她从网络搜到的两位数乘11的速算法，其口诀是：“头尾一拉，中间相加，满十进一”例如：①24×11=264.计算过程：24的十位与个位两数分开，中间相加，即2+4=6，最后结果是264；②68×11=748.计算过程：68的十位与个位两数分开，中间相加，即6+8=14，满十进一，最后结果是748．
(1)填空：①23×11= ______ ，②95×11= ______ ；
(2)若某个两位数的十位数字是a，个位数字是b(a+b<10)，将这个两位数与11相乘，根据上述方法得到积是一个三位数，请你用含a、b的代数式分别表示出这个三位数的百位、十位与个位上的数字；
(3)若某个两位数的十位数字是m，个位数字是n(m+n>10)，将这个两位数与11相乘，根据上述方法，请你用含m、n的代数式表示出所得的结果.(结果化为最简形式)
26.(本小题10分)
点A在数轴上所表示的数如图所示，将点A向左平移2个单位长度，得到点B的相反数，点P是数轴上一动点．

(1)点B表示的数是______ ；
(2)若点B在数轴上移动了m个单位长度得到点C，且AC=3，求m的值；
(3)若点D为AP的中点，点E为BP的中点，点P在运动过程中，线段DE的长度是否发生变化？若不发生变化，请你求出线段DE的长度；若发生变化，请你说明理由．
答案和解析
1.【答案】A
【解析】解：2÷(−13)
=2×(−3)
=−6，
故选：A．
根据有理数的除法运算法则计算即可求解．
本题考查有理数的除法，掌握除法法则是解题的关键．
2.【答案】B
【解析】解：A、圆柱的截面可能是圆、长方形等，此项不符合题意；
B、圆锥的截面可能是圆、三角形，不可能为长方形，此项符合题意；
C、长方体的截面可能是三角形、四边形、五边形、六边形，可能为长方形，此项不符题意；
D、三棱柱的截面可能为三角形、长方形，此项不符题意；
故选：B．
根据圆锥、圆柱、正方体、长方体的形状特点逐项判断即可得．
本题考查了几何体的截面，掌握各个几何体截面的不同形状是解答本题的关键．
3.【答案】C
【解析】解：A.−x2y和xy2，相同字母的指数分别不相等，不是同类项，故本选项不符合题意；
B.x2y和x2z的字母不相同，不是同类项，故本选项不符合题意；
C.−m2n3和−3n3m2的字母相同，相同字母的指数也分别相等，是同类项，故本选项符合题意；
D.−ab和abc的字母不完全相同，不是同类项，故本选项不符合题意；
故选：C．
根据同类项的定义逐个判断即可．
本题考查了同类项的定义，能熟记同类项的定义是解此题的关键，所含字母相同，并且相同字母的指数也分别相同的项叫同类项，常数项是同类项．
4.【答案】C
【解析】解：A.点O在直线AB上，正确，不符合题意；
B.点O在射线BA上，正确，不符合题意；
C.点O在线段AB上，不正确，符合题意；
D.射线OB和射线OA是同一条射线，正确，不符合题意，
故选：C．
根据线段，射线，直线的特点判断即可．
本题考查了线段，射线，直线的关系，熟练掌握各自的特点是解题的关键．
5.【答案】B
【解析】解：由正方体表面展开图的“相间、Z端是对面”可知，
“杭”与“您”相对，
“亚”与“欢”相对，
“会”与“迎”相对，
翻过第1格时，“杭”在下面，“亚”在右面，“会”在前面，
翻过第2格时，“杭”在后面，“亚”在右面，“会”在下面，
翻过第3格时，“亚”在下面，因此“欢”在上面，
故选：B．
根据正方体表面展开图的特征判断长相对的面，再根据翻滚的规律得出答案即可．
本题考查正方体相对两个面上的文字，掌握正方体表面展开图的特征是正确解答的前提．
6.【答案】B
【解析】解：∵∠MON=90°，
∴∠AOM=90°−∠BON，
∴2∠BON=180°−2∠AOM，
∵OC是∠MOB的平分线，
∴∠MOC=∠BOC=12∠MOB，
∴∠AOM=180°−2∠BOC=180°−2∠BON−2∠CON，
∴∠AOM=180°−(180°−2∠AOM)−2∠CON，
∴∠AOM=2∠NOC，
故选：B．
先求出2∠BON=180°−2∠AOM，利用角平分线的定义再求解，∠AOM=180°−2∠BOC=180°−2∠BON−2∠CON，从而可得答案．
本题考查了角的和差运算，角的平分线定义，熟练运用角的和差关系探究角与角之间的关系是解题的关键．
7.【答案】C
【解析】解：∵ab<0，a+b>0，
∴点M表示数a，点P表示数b或点M表示数b，点P表示数a，则点N表示数c，
∴由数轴可得c>0，
又∵ac>0，
∴a>0，
∴点P表示数a，点M表示数b，
故选：C．
由ab<0，a+b>0可推得点N表示数c，根据ac>0即知点P表示数a．
本题考查数轴，解题的关键是明确数轴的特点，能根据题目中的信息，判断各个数在数轴上对应哪一个点．
8.【答案】C
【解析】解：根据题意，得第一个图形的数量为6=(2×1+1)×2，
第2个图形的数量为10=(2×2+1)×2，
第3个图形的数量为14=(2×3+1)×2，
……，
故666个图形的数量为(2×666+1)×2=2666，
故选：C．
仔细观察图形，找到图形变化的规律，然后按规律求解即可．
本题考查了图形的变化类问题，解题的关键是能够找到图形的变化规律，然后求解．
9.【答案】7.5×105
【解析】解：750000=7.5×105．
故答案为：7.5×105．
根据科学记数法的定义和乘方的意义得到750000=7.5×105．
本题考查了科学记数法−表示较大的数：用a×10n(1≤a<10,n为正整数)表示数的方法叫科学记数法．也考查了乘方的意义．
10.【答案】两点之间线段最短
【解析】解：根据图的信息，三条线路不是最短的，理由是两点之间线段最短．
故答案为：两点之间线段最短．
根据两点之间距离(线段)最短即可求解．
本题考查两点之间线段最短的应用知识，属于基本能力考查．
11.【答案】>
【解析】解：∵52.15°=52°+0.15×60′=52°9′，
∴52°15′>52°9′，
∴52°15′>52.15°．
故答案为：>．
将角的度数换算成度分秒的形式，再进行比较即可得出结论．
本题考查的度分秒的换算以及角的大小比较，掌握将角的度数换算成度分秒的形式是关键．
12.【答案】1
【解析】解：要保持从上面和左面看到的形状图不变，
从左面看：，从上面看：
则从正面看，第二列第二层最多可以拿走1个，
故答案为：1．
根据左视图和俯视图求解即可．
本题考查了三视图的画法，综合分析两种视图是解题的关键．
13.【答案】(1.1x+66)
【解析】解：根据题意，得买A种型号机器的数量为2.6(15+x)÷2.6=(15+x)(台)，
买B种型号机器的数量为33−(15+x)=(18−x)(台)，
故总费用为2.6(15+x)+1.5(18−x)=(1.1x+66)万元，
故答案为：(1.1x+66)．
先求出买A种型号机器的数量，再求出求出买B种型号机器的数量即可求出购买购买A、B两种型号的机器的总费用．
本题考查列代数式，读懂题意列出算是是解题的关键．
14.【答案】解：(1)−6×|−13|÷(−2)−12
=−6×13×(−12)−1
=1−1
=0；
(2)−32−[8÷(−2)3−1]+12÷2×12
=−9−[8÷(−8)−1]+12×12×12
=−9−(−1−1)+3
=−9+2+3
=−4．
【解析】(1)按照先乘方，再乘除，最后计算加减的运算顺序计算即可；
(2)按照先乘方，再乘除，最后计算加减的运算顺序计算即可．
本题考查了有理数含乘方的运算，熟练掌握运算顺序是解题的关键．
15.【答案】解：如图所示，

证明：∵AC=AP+PC，AC=AB+BC，
∴AB+BC=AP+PC，
∴AB+a=AP+b，
∴AB=AP+b−a．
【解析】作法：1.作射线AP；2.在射线AP上截取PC=b；3.在线段CA上截取CB=a.A则AB即为所求．
本题考查尺规画线段以及线段的和差，解题的关键是掌握尺规作图的方法．
16.【答案】解：(1)根据题意，得这个五棱柱笔筒的外部共有6个面，15条棱．
(2)由题意得：此五棱柱每个侧面为长方形，侧棱为16厘米，底面边长为4厘米，有5个侧面，
∴4×16×5=320(cm2)，
答：制作此笔筒的侧面需要320cm2的材料．
【解析】(1)直接根据五棱柱的特征，即可求解．
(2)根据侧面是矩形，底面每条边长相等且等于4cm，侧棱为16cm，即可求解．
本题考查了棱柱的特征，侧棱，侧面积，熟练掌握棱柱的特征是解题的关键，
17.【答案】解：(1)一
(2)原式的倒数为：
(16−314+23−27)÷(−142)
=(16−314+23−27)×(−42)
=−7+9−28+12=−35+21=−14，
则原式=−114．
【解析】【分析】
此题考查了有理数的除法，熟练掌握除法法则是解本题的关键．
(1)我认为解法一是错误的；
(2)选择解法三求出值即可．
【解答】
解：(1)上述得到的结果不同，我认为解法一是错误的；
故答案为：一；
(2)见答案．
18.【答案】解：原式=−2xy+3x−6x+3xy+xy
=2xy−3x，
当x=−3，y=−2时，
原式=2×(−3)×(−2)−3×(−3)
=12+9
=21．
【解析】先根据整式加减混合运算法则进行计算，然后再代入求值即可．
本题主要考查了整式的加减--化简求值，熟练掌握运算法则是解本题的关键．
19.【答案】解：∵过多边形的一个顶点共有4条对角线，
故该多边形边数为4+3=7，
设这个正方形的边长为x，
则7x=56，
解得：x=8
即这个正多边形的边长为8．
【解析】本题主要考查了多边形的对角线，熟记多边形的对角线公式是解题的关键．
根据n边形从一个顶点出发可引出(n−3)条对角线，可求多边形的边数，再根据多边形的周长的定义可求这个多边形的各边长．
20.【答案】解：(1)由题意得：最重的一袋为30+2.5=32.5(千克)，最轻的一袋为30−3=27(千克)，
∵32.5−27=5.5(千克)，
∴最重的一袋比最轻的一袋重5.5千克；
(2)∵(−3)×1+1×2+0×3+2.5×8+(−2)×4+(−1.5)×2
=−3+2+0+20−8−3
=22−14
=8(千克)，
∴与标准重量比较，20袋大米总计超过8千克；
(3)这20袋大米总重为30×20+8=600+8=608(千克)，
∵608×10=6080(元)，
∴出售这20袋大米可卖6080元．
【解析】(1)利用正负数的意义从表格中找出最重的一袋和最轻的一袋的质量，将它们相减即可得出结论；
(2)利用表格数据计算代数和，通过观察计算结果即可得出结论；
(3)利用表格数据计算出20袋大米的总重，再乘以销售单价即可得出结论．
本题主要考查了正负数的意义，有理数的混合运算，正确理解正负数的意义是解题的关键．
21.【答案】解：(1)∵A=4x2−4xy+y2，3A−B=13x2−11xy−2y2
∴B=3A−(13x2−11xy−2y2)
A=4x2−4xy+y2
=12x2−12xy+3y2−13x2+11xy+2y2
=−x2−xy+5y2．
(2)∵x是单项式−6m2n的系数，y是−12的倒数，
∴x=−6，y=−2，
∴B=−x2−xy+5y2=−(−6)2−(−6)×(−2)+5(−2)2
=−36−12+20=−28．
【解析】(1)根据题意，运用整式的加减运算法则计算求解即可．
(2)根据题意，确定x的值，y得值，代入计算求解即可．
本题考查整式的加减，单项式的系数，倒数，求代数式的值，熟练掌握整式的加减运算是解题的关键，
22.【答案】解：AD=2CE.理由如下：
设AB=10x，
∵C为线段AB的中点，
∴AC=BC=5x，
∵AD：BD=3：2，
∴AD=35AB=6x,BD=25AB=4x，
∵E为线段DB的中点，
∴DE=BE=12BD=2x，
∴CE=BC−DE=3x，
∴AD=2CE．
【解析】设AB=10x，根据题意用含x的代数式表示线段AD，线段CE，后确定数量的关系即可．
本题考查了线段的中点，线段的和差倍比，熟练掌握掌握线段的中点是解题的关键．
23.【答案】(y−15)
【解析】解：(1)根据题意，得y=3×5+l小长方形的长，
故l小长方形的长=(y−15)cm，
故答案为：(y−15)．
(2)设阴影A的长为m，宽为n，阴影B的长为p，宽为q，根据l小长方形A的长=m=y−15(cm)，n=x−10(cm)，p=15(cm)，q=x−(y−15)=(x−y+15)(cm)，
∴阴影部分A的周长为2(m+n)=2(y−15+x−10)=(2x+2y−50)(cm)，
阴影部分B的周长为2(p+q)=2(x−y+15+15)=(2x−2y+60)(cm)，
∴阴影部分A和B的周长之和为(2x+2y−50+2x−2y+60)=(4x+10)(cm)．
(3)设阴影A的长为m，宽为n，阴影B的长为p，宽为q，根据l小长方形A的长=m=y−15(cm)，n=x−10(cm)，p=15(cm)，q=x−(y−15)=(x−y+15)(cm)，
∴阴影部分A的面积为mn=(y−15)(x−10)=(xy−10y−15x+150)(cm2)，
阴影部分B的面积为pq=15(x−y+15)=(15x−15y+225)(cm2)，
∴阴影部分A和B的面积之和为(xy−10y−15x+150+15x−15y+225)=(xy−25y+375)(cm2).
当y=30时，(30x−375)(cm2).
(1)观察图形，由大长方形的长等于小长方形的宽的3倍与小长方形的长的和计算即可．
(2)设阴影A的长为m，宽为n，阴影B的长为p，宽为q，根据l小长方形A的长=m=y−15(cm)，n=x−10(cm)，p=15(cm)，q=x−(y−15)=(x−y+15)(cm)，根据题意计算即可．
(3)设阴影A的长为m，宽为n，阴影B的长为p，宽为q，根据l小长方形A的长=m=y−15(cm)，n=x−10(cm)，p=15(cm)，q=x−(y−15)=(x−y+1745)(cm)，根据题意计算即可．
本题考查了列代数式以及整式的混合运算，掌握整式的混合运算法则是解题的关键．
24.【答案】解：(1)∵OB是∠AOC的平分线，OD是∠COE的平分线，
∠AOB=40°，∠DOE=25°，
∴∠BOC=∠AOB=40°，∠COD=∠DOE=25°，则∠COE=2∠DOE=50°，
∴∠BOE=∠BOC+∠COE=40°+50°=90°．
(2)∵OD是∠COE的平分线，∠COD=20°，
∴∠COE=2∠COD=2×20°=40°，
∵∠AOE=120°，
∴∠AOC=∠AOE−∠COE=120°−40°=80°，
∵OB是∠AOC的平分线，
∴∠AOB=12∠AOC=12×80°=40°．
【解析】(1)根据角平分线的定义以及角的和差关系进行计算即可．
(2)根据角平分线的定义进行计算即可．
本题考查角平分线，熟练掌握角的和差关系、角平分线的定义是解决本题的关键．
25.【答案】253 1045
【解析】解：(1)23×11，
23的十位与个位两数分开，中间相加，即2+3=5，最后结果是253，
95×11，
95的十位与个位两数分开，中间相加，即9+5=14，满十进一，最后结果是1045，
故答案为：253；1045；
(2)依题意得：
这个三位数的百位为：a，
这个三位数的十位为：(a+b)，
这个三位数的个位为：b
(3)依题意得：
100(m+1)+10(m+n−10)+n
=100m+100+10m+10n−100+n
=110m+11n．
(1)根据口诀“头尾一拉，中间相加，满十进一”即可求解；
(2)根据口诀：“头尾一拉，中间相加，满十进一”，分别表示出这个三位数的百位、十位及个位上的数字即可求解；
(3)根据口诀：“头尾一拉，中间相加，满十进一”表示出这个数，再利用整式的加减运算即可求解．
本题考查了数字规律探索、整式加减的应用、列代数式，理解口诀，灵活应用口诀是本题解题关键．
26.【答案】−2
【解析】解：(1)∵点A表示的数是4，
∴平移左减2两个单位得到的数是2，
其相反数即为点B表示的数．
∴点B表示的是−2，
故答案为：−2．
(2)∵点A表示的数是4，AC=3，
∴|4−xC|=3，
∴4−xC=3或4−xC=−3，
解得xC=1或xC=7，
∵点B表示的是−2，
∴向右平移1−(−2)=3或7−(−2)=9，
故m=3或m=9．
(3)设点P表示的数是xP，点D表示的数是xD，点E表示的数是xE，
∵点B表示的是−2，点A表示的数是4，
当xP<−2时，xD=4+xP2，xE=−2+xP2，
∴DE=xD−xE=4+xP2−−2+xP2=3；
当−2≤xP≤4时，xD=4+xP2，xE=−2+xP2，
∴DE=xD−xE=4+xP2−−2+xP2=3；
当xP>4时，xD=4+xP2，xE=−2+xP2，
∴DE=xD−xE=4+xP2−−2+xP2=3；
故线段DE的长度不变，且为3．
(1)根据点A表示的数是4，平移左减2两个单位得到的数是2，其相反数即为点B表示的数．
(2)根据点A表示的数是4，AC=3，确定点C表示的数，再计算平移单位数即可．
(3)分xP<−2，−2≤xP≤4，xP>4三种情况计算即可．
本题考查了数轴上的动点问题，两点间的距离，数轴上的平移，熟练掌握两点间的距离是解题的关键，与标准质量的差值(单位：千克)
−3
1
0
2.5
−2
−1.5
袋数
1
2
3
8
4
2