

期末经典题型检测卷2023-2024学年人教版数学七年级上册
展开一、单选题
1.下列各数中,最小的是( )
A.B.C.D.
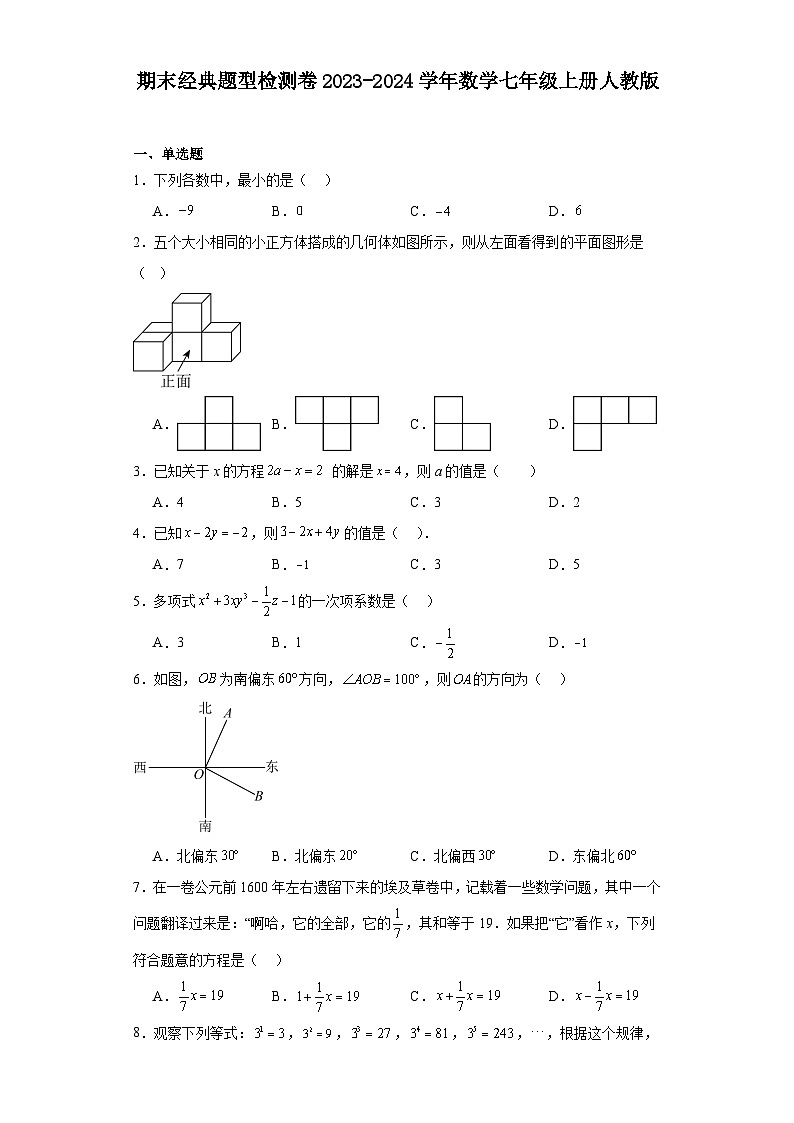
2.五个大小相同的小正方体搭成的几何体如图所示,则从左面看得到的平面图形是( )
A.B.C.D.
3.已知关于x的方程 的解是,则a的值是( )
A.4B.5C.3D.2
4.已知,则的值是( ).
A.7B.C.3D.5
5.多项式的一次项系数是( )
A.3B.1C.D.
6.如图,为南偏东方向,,则的方向为( )
A.北偏东B.北偏东C.北偏西D.东偏北
7.在一卷公元前1600年左右遗留下来的埃及草卷中,记载着一些数学问题,其中一个问题翻译过来是:“啊哈,它的全部,它的,其和等于19.如果把“它”看作x,下列符合题意的方程是( )
A.B.C.D.
8.观察下列等式:,,,,,,根据这个规律,则的末尾数字是( )
A.0B.2C.9D.8
二、填空题
9.若关于x,y的单项式与的和仍为单项式,则的值为 .
10.已知线段,在直线上有一点,且,若点,分别是线段,的中点,则线段的长为 .
11.已知是关于x的一元一次方程,则m的值为 .
12.某商品进价为n元/件,在销售旺季,该商品售价较进价高.销售旺季过后.将该商品按售价打8折促销.这时一件商品的售价为 元/件.
13.计算: .
14.数在数轴上所对应点如图所示:化简 .
15.将正方体骰子(相对面上的点数分别为1和6,2和5,3和4)放置于水平桌面上,如图①,将骰子向右翻滚;然后在桌面上按逆时针方向旋转,则视作完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成9次变换后,骰子朝上一面的点数是 .
16.如图1,点A,B,C是数轴上从左到右排列的三个点,对应的数分别为,b,6,某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对齐刻度,点C对齐刻度.则数轴上点B所对应的数b为 .
三、解答题
17.计算:
18.解下列方程:
(1);
(2).
19.已知多项式.若多项式的值与字母x的取值无关,求的值.
20.如图,在直线上任取一点O,过点O作射线,平分,平分,当时,求的度数.
21.2023年9月23日-10月8日,第十九届亚洲运动会在中国杭州举行,其吉祥物“宸宸、琮琮和莲莲”倍受广大群众喜爱.新年将至,学校计划订购一批吉祥物的挂件和徽章.经调查发现,同一款式的挂件和徽章在甲、乙两家商店标价均相同,其中挂件每个标价40元,徽章每个标价20元.同时,两家商店分别开展不同的新年促销活动优惠方式如下:
甲商店:买一个挂件送一个徽章;
乙商店:挂件和徽章都按8折(标价的80%)出售.
如果学校计划订购挂件30个,徽章若干(多于30个),
(1)当订购35个徽章时,如果在甲商店订购,费用需__________元;
(2)当订购多少个徽章时,在甲、乙两家商店分别订购的费用相同;
(3)当订购100个徽章时,如果甲、乙两家商店可以自由选择,请设计一种最省钱的订购方案,并说明理由.
22.如图1,在直线上取点,从点引射线.直角三角尺的直角顶点在点处(注:),现将直角三角尺绕点逆时针转动,起始时三角尺的边在直线上.
(1)图1中的度数为______.
(2)如图2,若平分,请说明所在射线是的平分线.
(3)记为,若满足,求的度数.
23.已知数轴上点表示的数是0,A,两点表示的数分别是,,且满足.动点从点A出发,以每秒1个单位长度的速度向点运动,设运动时间为秒,点运动到点时停止.
(1)填空∶①________,________.
②点表示的数为________(用含有的式子表示);
③当的值为________时,点停止运动;
(2)当点在线段上运动时,若为的中点,为的中点,试判断在点运动的过程中,线段的长度是否发生变化.如果发生变化,请说明理由,如果不发生变化,请求出线段的值;
(3)当点运动到点时,动点开始从点A出发,以每秒个单位长度的速度在A,两点之间往返运动.动点仍按照原来的速度运动,直至点停止运动,点也停止运动.当,两点之间的距离为时,直接写出的值.
24.【阅读】计算的值,令,则,因此,所以,即.
仿照以上推理计算:的值.
参考答案:
1.A
【分析】本题考查了有理数大小比较,利用数轴将各个数表示出来,是解答本题的关键.
根据有理数的性质,将选项中每个数字在数轴上表示出来,得到最小的数是,由此得到答案.
【详解】解:根据题意,
将选项中每个数字在数轴上表示出来,如图所示:
,
最小的数是,
故选:.
2.C
【分析】本题考查从从不同方向看几何体,理解从左面看几何体的意义即可求解.
【详解】解:根据搭成的几何体,从左面看得到的平面图形是,
故选:C.
3.C
【分析】本题主要考查了解一元一次方程,一元一次方程解的定义,根据一元一次方程的解是使方程左右两边相等的未知数的值把代入原方程求出a的值即可.
【详解】解:∵关于x的方程 的解是,
∴,
∴,
故选C.
4.A
【分析】本题考查了代数式求值,解决本题的关键是利用整体思想.根据整体代入思想即可求解.
【详解】解:
,
故选:A .
5.C
【分析】本题主要考查了多项式的相关定义,几个单项式的和的形式叫做多项式,每个单项式叫做多项式的项,不含字母的项叫做常数项,多项式里,次数最高项的次数叫做多项式的次数,据此求解即可.
【详解】解:多项式的一次项是,它的系数是,
故选C.
6.B
【分析】本题考查了方位角,熟练掌握方位角的判断方法是解题的关键,利用角的和差先求出的度数,然后即可得解.
【详解】解:如图,
为南偏东方向,
,
,
,
的方向为北偏东,
故选:B.
7.C
【分析】本题主要考查了一元一次方程的应用,解题的关键是理解题意,根据等量关系列出方程.
【详解】解:∵它的全部,它的,其和等于19,
∴把“它”看作x,可以列方程:.
故选:C.
8.B
【分析】本题考查了实数类规律探究,能够发现规律是解题的关键;
首先得出个位数字变化规律,进而得出的结果的个位数字即可.
【详解】,,,,,,
个位数字4个数为一组循环,分别为3,9,7,1,
的个位数字为0,
,
的个位数字为2,
故选:B
9.
【分析】本题考查了单项式的定义,同类项的判断,先根据两个单项式的和仍为单项式可得到这两个单项式为同类项,进而可得到的值,然后代入即可得到结果,判断两个单项式为同类项是解题的关键.
【详解】解:∵关于x,y的单项式与的和仍为单项式,
∴,解得,
∴,
故答案为:.
10.
【分析】本题主要考查两点间的距离,线段中点的定义,注意分类讨论.
可分两种情况:当点C在线段上时,当点C在射线上时,根据两点间的距离先求解的长,再根据线段中点的定义可求解的长.
【详解】解:当点C在线段上时,如图,
∵,,
∴,
∵点M、N分别是线段、的中点,
∴,
当点C在射线上时,如图,
∵,,
∴,
∵点M、N分别是线段、的中点,
,
故答案为:.
11.1
【分析】本题考查了绝对值,一元一次方程的定义,熟练掌握一元一次方程的定义是解题的关键.根据一元一次方程的定义,只含有一个未知数,并且未知数的最高次数是1的整式方程,进行计算即可解答.
【详解】解:由题意得:
且,
∴或1且,
∴.
故答案为:1.
12.
【分析】本题考查了用字母表示数.先求出旺季的售价,再求出8折促销后的售价即可.
【详解】解:根据题意可得:旺季的售价为,
将该商品按售价打8折促销后的售价为,
故答案为:.
13.
【分析】此题考查了有理数的加减混合运算,绝对值的化简等知识,原式利用绝对值的意义进行化简化简,再进行加减计算即可得到结果.
【详解】解:
.
故答案为:
14.
【分析】本题主要考查了实数与数轴,绝对值的意义,利用数,,在数轴上所对应点的位置,判断出,的符号是解题的关键.
利用数,,在数轴上所对应点的位置,判断出,的符号,再利用绝对值的意义化简求值即可.
【详解】解:由题意得:,,
,,
.
故答案为:.
15.3
【分析】本题考查了规律型:图形的变化,根据题意得到连续3次变换是一个循环,然后根据9被3整除,即可确定骰子朝上一面的点数.
【详解】解:根据题意可知,第一次变换骰子朝上一面的点数是5;
第二次变换骰子朝上一面的点数是6;
第三次变换骰子朝上一面的点数是3;
第四次变换骰子朝上一面的点数是5;
⋯⋯,
发现可得连续3次变换是一循环.
.
所以得到第3次变换后的图形,即按上述规则连续完成9次变换后,骰子朝上一面的点数是3.
故答案为:3.
16.0
【分析】本题考查的是数轴的概念,有理数四则混合运算的应用,解题的关键是确定数轴上的单位长度等于多少厘米.
数轴上A、C两点间的单位长度是,点C对齐刻度,所以数轴的单位长度是,的长度是,除以得在数轴上的单位长度.
【详解】∵,
∴数轴的单位长度是,
∵,
∴在数轴上A,B的距离是3个单位长度,
∴点B所对应的数b为.
故答案为:0.
17.
【分析】本题主要考查有理数的混合运算,原式先计算乘方和括号内的,再把除法转换为乘法,计算乘法即可.
【详解】解:
.
18.(1)
(2)
【分析】本题主要考查解一元一次方程,
(1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.
【详解】(1)解:
移项得,
合并同类项得,;
(2)解:
去分母得,
去括号得,
移项,合并同类项得,
系数化为1得,.
19.
【分析】此题考查了整式的加减—化简求值,熟练掌握运算法则是解本题的关键.原式去括号合并后,根据多项式的值与字母x取值无关,确定出m与n的值即可
【详解】解:原式
由多项式的值与字母的取值无关,得到
解得∶
20.
【分析】本题主要考查了角平分线的定义,先根据角平分线的定义得到,再由平角的定义求出,进而由角平分线的定义得到.
【详解】∵平分,,
∴,
∴,
∵平分,
∴.
21.(1)1300
(2)190
(3)最省钱的订购方案为在甲商店购买挂件30个,徽章30个,在乙商店购买徽章70个,理由见解析
【分析】本题主要考查了有理数的混合运算,一元一次方程的应用:
(1)用30个挂件的费用加上5个徽章的费用,即可求解;
(2)设当订购x个徽章时,在甲、乙两家商店分别订购的费用相同,根据题意,列出方程,即可求解;
(3)分别求出在甲商店购买费用;在乙商店购买费用;在甲商店购买挂件30个,徽章30个,在乙商店购买徽章70个的费用,即可求解.
【详解】(1)解:元,
即在甲商店订购,费用需1300元,
故答案为:1300;
(2)解:设当订购x个徽章时,在甲、乙两家商店分别订购的费用相同,根据题意得:,
解得:,
答:当订购190个徽章时,在甲、乙两家商店分别订购的费用相同;
(3)解:最省钱的订购方案为在甲商店购买挂件30个,徽章30个,在乙商店购买徽章70个,理由如下:
若在甲商店购买,费用为元,
若在乙商店购买,费用为元,
若在甲商店购买挂件30个,徽章30个,在乙商店购买徽章70个,费用为
元,
∵,
∴最省钱的订购方案为在甲商店购买挂件30个,徽章30个,在乙商店购买徽章70个.
22.(1)
(2)见解析
(3)或
【分析】本题考查几何图形中角度的计算,角平分线的定义,注意分类讨论是解题的关键.
(1)根据求解;
(2)根据角平分线的定义及角的和差关系可得;
(3)分在内部与外部两种情况,结合,,根据列式求出,进而可得的度数.
【详解】(1)解:,,
,
故答案为:;
(2)证明:平分,
,
,
,
,
,
即所在射线是的平分线;
(3)解:分两种情况:
当在内部时,如图:
,,
,
,
,
,
解得,
;
当在外部时,如图:
,,
,
,
,
,
解得,
;
综上可得,的度数为或.
23.(1)①,15;②;③21;
(2)线段的长度不发生变化,为3
(3)或
【分析】本题考查了一元一次方程的应用,数轴上两点间的距离,非负数的性质,找到相等关系是解题的关键.
(1)①根据非负数的性质求解;②根据向右运动用加法列式表示;③根据“时间路程速度”计算;
(2)根据两点之间的距离公式求解;
(3)根据两点之间的距离公式求解.
【详解】(1)解:①,
,
,
故答案为:,15;
②点P表示的数为:,
故答案为:;
③,
故答案为:21;
(2)解:线段的长度不发生变化,为3;理由:
M表示的数为:,N表示的数为:,
;
(3)解:,即点运动到点需要14秒,
当时,点从向运动,点表示的数为,
则,
解得:或(不合题意,舍去),
当时,点从向运动,点表示的数为,
则,
解得:或(不合题意,舍去),
综上,当或时,P、Q相距.
24.
【分析】本题考查了规律问题和有理数的混合运算,模仿例题设辅助未知数,即可解决问题.
【详解】解:设①,
则②,
∴得,,
∴,
即.
苏科版2023-2024学年七年级上册期末经典题型检测卷(含解析): 这是一份苏科版2023-2024学年七年级上册期末经典题型检测卷(含解析),共22页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
期末经典题型检测卷2023-2024学年人教版数学八年级上册: 这是一份期末经典题型检测卷2023-2024学年人教版数学八年级上册,共24页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
期末经典题型检测卷2023-2024学年青岛版数学七年级上册: 这是一份期末经典题型检测卷2023-2024学年青岛版数学七年级上册,共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












