期末经典题型检测卷2023-2024学年数学九年级上册青岛版

这是一份期末经典题型检测卷2023-2024学年数学九年级上册青岛版，共26页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．已知的直径为，点A到圆心的距离为，则点A与的位置关系是（ ）
A．点A在圆内B．点A在圆上C．点A在圆外D．无法确定
2．在中，，，，那么等于（ ）
A．B．C．D．
3．参加一次商品展销会的每两家公司之间都签订了一份合同，所有公司共签订了45份合同．设有家公司参加商品展销会，则所列方程正确的是（ ）
A．B．
C．D．
4．如图，线段是的直径，是的弦，过点C作的切线交的延长线于点E，，则（ ）
A．B．C．D．
5．如图，在中，，斜边上的高，矩形的边在边上，顶点G、F分别在边、上，如果正好经过的重心，那么的积等于（ ）
A．4B．1C．D．
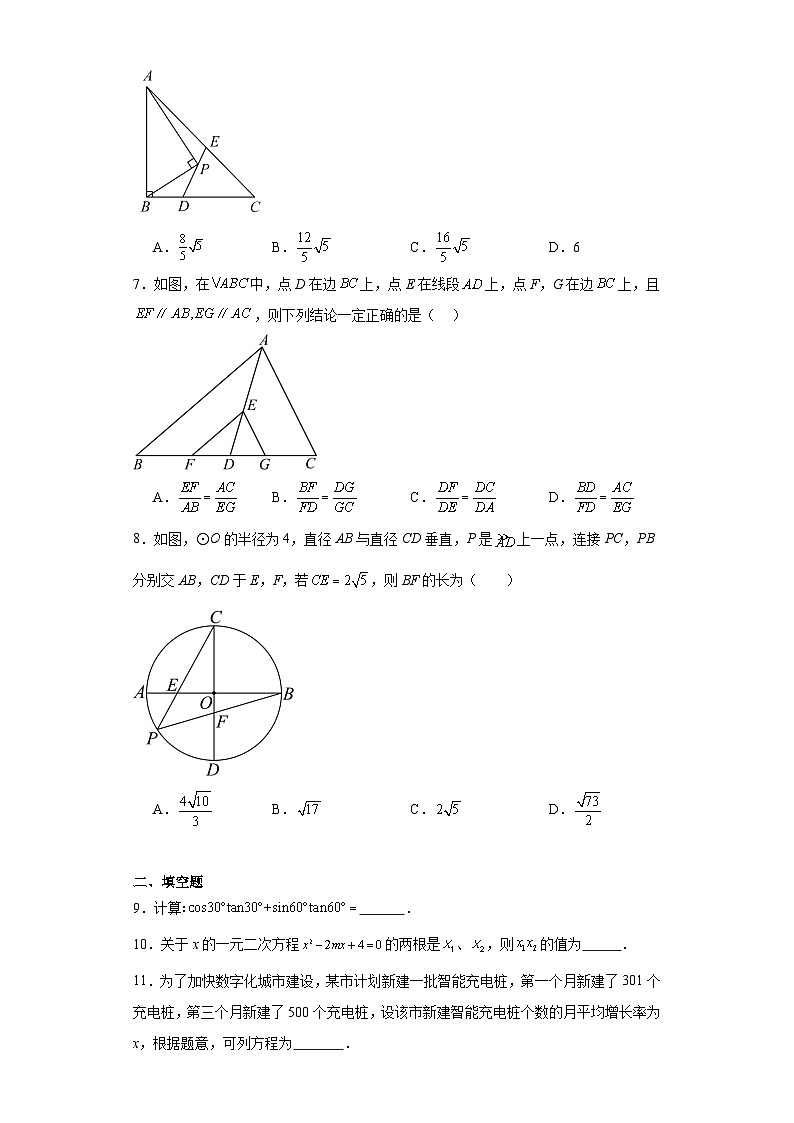
6．如图，中，，，D在边上，且，P为形内一点，满足，直线交于点E，当最大时，的长是（ ）
A．B．C．D．6
7．如图，在中，点D在边上，点E在线段上，点F，G在边上，且，则下列结论一定正确的是（ ）
A．B．C．D．
8．如图，⊙O的半径为4，直径AB与直径CD垂直，P是上一点，连接PC，PB分别交AB，CD于E，F，若，则BF的长为（ ）

A．B．C．D．
二、填空题
9．计算∶ ．
10．关于x的一元二次方程的两根是、，则的值为 ．
11．为了加快数字化城市建设，某市计划新建一批智能充电桩，第一个月新建了301个充电桩，第三个月新建了500个充电桩，设该市新建智能充电桩个数的月平均增长率为x，根据题意，可列方程为 ．
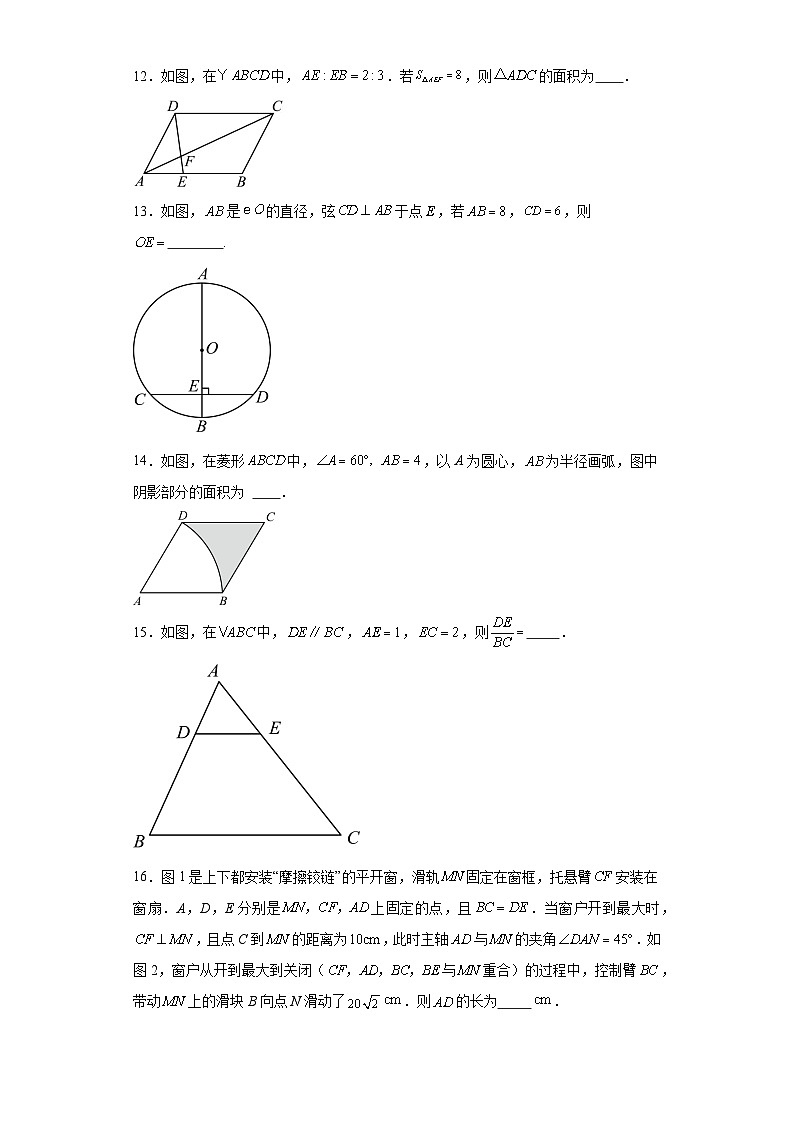
12．如图，在中，．若，则的面积为 ．
13．如图，是的直径，弦于点，若，，则 .
14．如图，在菱形中，，以A为圆心，为半径画弧，图中阴影部分的面积为 ．
15．如图，在中，，，，则 ．
16．图1是上下都安装“摩擦铰链”的平开窗，滑轨固定在窗框，托悬臂安装在窗扇．A，D，E分别是上固定的点，且．当窗户开到最大时，，且点C到的距离为，此时主轴与的夹角．如图2，窗户从开到最大到关闭（与重合）的过程中，控制臂，带动上的滑块B向点N滑动了．则的长为 ．
三、解答题
17．解下列方程
(1)；
(2)；
(3)；
(4)．
18．如图，在矩形中，E是的中点，，垂足为F．
(1)求证：；
(2)若，求的长．
19．某学校在“美化校园，幸福学习”活动中，计划利用如图所示的直角墙角（阴影部分，两边足够长），用长的篱笆围成一个矩形花园（篱笆只围两边）．
(1)若花园的面积为，求的长；
(2)若在直角墙角内点P处有一棵桂花树，且到墙的距离为，若要将这棵树围在矩形花园内（含边界，不考虑树的粗细），问该花园的面积能否为？若能，求出的长；若不能，请说明理由．
20．如图，为的直径，交于点C，D为上一点，延长交于点E，延长至F，使，连接．
(1)求证：为的切线；
(2)若且，求的半径．
21．如图，在边长为6的正方形中，点是线段上一点，过点作交的延长线于点，连接交于点，过点作于点，交于点，连接，．
(1)求证：；
(2)求证：；
(3)当点是线段的三等分点时，请直接写出的长．
22．随着人民生活水平的日益提高，许多农村的房屋普遍进行了改造，小明家改造时在门前安装了一个遮阳棚，如图，在侧面示意图中，遮阳篷长为4米，与墙面的夹角，靠墙端A离地高为3米，当太阳光线与地面的夹角为时，求阴影的长．（结果精确到米；参考数据：）
23．在边长为6的菱形中，动点从点出发，沿向终点运动，连接交于点．
① ②
(1)如图①，当点在边上时，连接．
①求证：；
②若，，，求点到的距离及的值；
(2)如图②，若，记点运动所经过的路程为．试问：为何值时，为等腰三角形．
参考答案：
1．C
【分析】本题考查了对点与圆的位置关系的判断．根据点与圆的位置关系判断即可．
【详解】解：∵的直径为，
∴的半径为，
∵点A到圆心的距离为，
∴点A与的位置关系是点A在圆外．
故选：C
2．D
【分析】本题考查了三角函数的计算，根据正切的定义计算选择即可．
【详解】∵，，，
∴，
故选D．
3．A
【分析】本题考查了由实际问题抽象出一元二次方程．每家公司都与其他公司签定了一份合同，设有x家公司参加，则每个公司要签份合同，签订合同共有份．
【详解】解：设有x家公司参加，依题意，得
．
故选：A．
4．B
【分析】本题考查圆周角定理，切线的性质，根据是的切线可得，进而求出，根据同弧所对的圆周角等于圆心角的一半即可求解．
【详解】解：如图，连接，
是的切线，
，
，
，
，
故选B．
5．B
【分析】本题考查了三角形的重心，相似三角形的判定和性质，矩形的性质，设的重心是，连接，延长交于，由三角形的重心的性质可得，再结合矩形的性质和平行线分线段成比例及余角的性质证明，即可推出．
【详解】解：设的重心是，连接，延长交于，
，
四边形是矩形，
，，
，
，
，
，
，
，
，
，
，
，
，
，
，，，，
，
．
故选：B．
6．C
【分析】本题主要考查轨迹和最值问题，涉及勾股定理、切线定理以及相似三角形的判定和性质，根据题意得点P在以为直径的圆上，当最大时，线段与相切，取的中点，连接和，可证明，得，在中可求得答案．
【详解】解：∵，
∴点P在以为直径的圆上，
取的中点，连接和，如图，
当最大时，线段与相切，则，
∵，，
∴，
∵，
∴，
∵，，
∴
∴，
在中，，
则，解得，
那么，．
故选：C．
7．D
【分析】本题主要考查了相似三角形的判定和性质，平行线分线段成比例，解题的关键是掌握相似三角形对应边成比例．根据题意得出，再逐个判断即可．
【详解】解：A、∵，
∴，
∴，
∴，故A不正确，不符合题意；
B、∵，
∴，
∴，故B不正确，不符合题意；
C、∵，
∴，
∴，则，
当时，，故C不正确，不符合题意；
D、∵，
∴，
∴，
∴，故D正确，符合题意；
故选：D．
8．A
【分析】本题主要考查圆周角定理、解直角三角形等知识，连接BD，过点F作，证明，设，则，构建方程求出m，即可求解.
【详解】解：连接BD，过点F作于H．

∵，
∴，
∵，，
∴，
∴，
∵，
∴，
设，则，
∵，，
∴，
∵，
∴，
∴，
∴，
∴，
∴．
故选：A．
9．2
【分析】本题考查的是特殊角的三角函数值的混合运算，先根据特殊角的三角函数值得到原式化为，然后进行二次根式的混合运算即可．熟记特殊角的三角函数值是解本题的关键．
【详解】解：原式
．
故答案为2．
10．4
【分析】本题主要考查了一元二次方程根与系数的关系，对于一元二次方程，若是该方程的两个实数根，则，由此可得答案．
【详解】解：∵关于x的一元二次方程的两根是、，
∴，
故答案为：4．
11．
【分析】本题考查一元一次方程实际应用．根据题意设月平均增长率为x，第一个月到第三个月经过了2个月，根据题干即可列出方程．
【详解】解：∵设该市新建智能充电桩个数的月平均增长率为x，
又∵第一个月新建了301个充电桩，第三个月新建了500个充电桩，
∴方程为：，
故答案为：．
12．70
【分析】本题考查平行四边形的性质，相似三角形的判定和性质．根据平行四边形的性质，得到，进而得到，得到，，得到，根据同高三角形的面积比等于底边比求出，再利用，求解即可．
【详解】解：∵，
∴．
∵四边形是平行四边形，
∴，
∴，，
∴，，
∴，
∵，
∴，，
∴．
故答案为：70．
13．
【分析】本题考查了垂径定理，熟记定理内容是解题关键．连接，根据即可求解．
【详解】解：连接，如图所示；
∵是的直径，弦于点，
∴
∵，
∴，
故答案为：
14．．
【分析】本题考查了菱形面积和扇形面积的计算，根据“阴影面积=菱形面积-扇形面积”求解即可．
【详解】解：过点作，如图，
∵四边形是菱形，
∴，
∴，
∴菱形的面积为：；
扇形的面积为：
阴影部分的面积为：，
故答案为：．
15．
【分析】本题考查了相似三角形的判定和性质，根据，得到，得到，由，， 即可求．
【详解】解：，
，
，
，，
，
，
故答案为：．
16．
【分析】根据题意，分别求出即可解决问题．本题考查解直角三角形的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
【详解】解：由题意四边形是平行四边形，
∴，
∵当窗户开到最大时，，，
∴，
∵点C到的距离为，
∴，
∴，
∵户从开到最大到关闭，滑块B向点N滑动了，
由题意，，
∵，
∴，
∴，
故答案为：
17．(1)，
(2)，
(3)，
(4)，
【分析】（1）变形后利用开平方法解方程即可；
（2）变形后利用因式分解法解方程即可；
（3）利用因式分解法解方程即可；
（4）利用因式分解法解方程即可．
此题考查了解一元二次方程，熟练掌握一元二次方程的解法并灵活选择是解题的关键．
【详解】（1）
解：，
，
∴，
∴，
（2），
解：，
，
或，
所以，.
（3），
解：，
∴或，
解得，.
（4），
解：，
∴或，
∴，
18．(1)证明见解析
(2)
【分析】（1）利用矩形的性质得到，再利用三角形内角和定理和垂线的定义证明，即可证明；
（2）先利用矩形的性质得到，再由线段中点的定义得到，则可利用勾股定理求出，再由相似三角形的性质得到，据此代值计算即可．
【详解】（1）证明：∵四边形是矩形，
∴，
∵，
∴，
∴，
∴，
∴；
（2）解：∵四边形四边形是矩形，，
∴，
∵E是的中点，
∴，
∵，
∴，
∵，
∴，即，
∴．
【点睛】本题主要考查了矩形的性质，勾股定理，相似三角形的性质与判定，三角形内角和定理等等，证明是解题的关键．
19．(1)5米或15米
(2)不能，理由见解析
【分析】本题主要考查了一元二次方程的实际应用，正确理解题意找到等量关系列出方程是解题的关键．
（1）米，则米，由矩形面积公式得出方程，解方程即可；
（2）根据题意可得方程，求出x的值，然后再根据P处这棵树是否被围在花园内进行分析即可．
【详解】（1）解：米，则米，
由题意得：，
解得：，，
答：的长为5米或15米；
（2）解：花园的面积不能为，理由如下：
米， 米，
由题意得：，
解得：，
当时，，
即当米，米米，这棵树没有被围在花园内，
将这棵树围在矩形花园内（含边界，不考虑树的粗细），则花园的面积不能为．
20．(1)见解析
(2)的半径为3
【分析】本题考查了切线的判定与性质，勾股定理，等腰三角形的性质，熟记切线的判定定理是解题的关键．
（1）连接，根据等边对等角结合对等角相等即可推出结论；
（2）设的半径，则，，在中，由勾股定理得得出方程求解即可．
【详解】（1）证明：如图，连接，
∵，
∴，
∵，
∴，
∵，，
∴，
即，
∴，
∵是半径，
∴为的切线；
（2）解：设的半径，则，
∴，
在中，由勾股定理得，
，
∴，
解得，或（舍去），
∴的半径为3．
21．(1)见解析
(2)见解析
(3)或3
【分析】（1）证明是等腰直角三角形，根据直角三角形斜边中线的性质可得，即可得证；
（2）先证明和是等腰直角三角形，可得，证明，即可得证；
（3）连接，由全等的性质及等腰三角形的性质可得，设，则，，分两种情况讨论：①当时，②当时，在中，利用勾股定理，建立方程求解即可．
【详解】（1）证明：，
，
四边形是正方形，
，，，
，，
，
，
，
，
，
在中，
，
，
；
（2）证明：，，
，，
是等腰直角三角形，
，
又，
，
为等腰直角三角形，
，，
，
四边形中，，
A、H、E、D共圆，
，
，
，
，
又，，
，
，
，
；
（3）解：如图，连接，
，，
，，
，
，
，
设，则，，
正方形的边长为6，点是线段的三等分点，
①当时，则，
在中，，即，
解得：，
，
②当时，则，
在中，，即，
解得：，
，
当点是线段的三等分点时，的长为或3．
【点睛】本题考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，相似三角形的判定和性质，勾股定理，熟练掌握知识点并灵活运用是解题的关键．
22．
【分析】本题主要考查了解直角三角形的实际应用，矩形的性质与判定，过点作于点，于点，则四边形是矩形，据此可得，解得到，，进而求出，再解得到，则．
【详解】解：如图所示，过点作于点，于点，则四边形是矩形，
∴，
在中，，
∴，，
∴，
在中，，
∴，
∴阴影的长为．
23．(1)①证明见解析；②点到的距离为，；
(2)或或
【分析】（1）①如图①，根据菱形的性质，证明即可．
②提示：如图①，作交的延长线于点．由，结合特殊角的三角函数计算即可．
(2)，菱形是正方形．．分三种情形求解即可．
【详解】（1）①如图．四边形是菱形，
，．
又∵，
．
②作交的延长线于点．
由．，，
得．
在中，．
即点到的距离为．
在中，．
．
在中，，
由①知，，
．
．
（2），
菱形是正方形．
．
下面分三种情形：
（Ⅰ）若，则．
此时，点恰好与点重合，得．
（Ⅱ）若，则．
此时，点恰好与点重合，得．
（Ⅲ）如图②，若，则．
②
，
．
又，
．
．
，
．
故．
综上所述，当或或时，是等腰三角形．
【点睛】本题考查了菱形的性质，正方形的判定和性质，三角函数的应用，特殊角的三角函数值，三角形全等的判定和性质，等腰三角形的判定，分类思想，熟练掌握菱形的性质，三角函数的定义，等腰三角形的判定，三角形全等的判定是解题的关键．