



专题突破卷20 立体几何的截面问题-备战2024年高考数学一轮复习高分突破(新高考通用)
展开1.作出截面图
1.如图,直四棱柱的底面为正方形,为的中点.
(1)请在直四棱柱中,画出经过三点的截面并写出作法(无需证明).
(2)求截面的面积.
【答案】(1)图形见解析
(2)
【分析】(1)取的中点,连接、、、,则四边形即为所求;
(2)依题意可得四边形为菱形,连接,,求出,,即可得解.
【详解】(1)取的中点,连接、、、,
则四边形即为过点、和的平面截直四棱柱所得截面;
取的中点,连接、,因为为的中点,为直四棱柱,底面为正方形,
所以且,且,所以且,
所以为平行四边形,所以,
又且,所以为平行四边形,所以,
所以,即、、、四点共面.
(2)在直四棱柱中,,、分别为、的中点,
所以,
所以四边形为菱形,连接,,则,
又,,
所以.
2.如图,在棱长为2的正方体中,E,F,G分别为的中点.过作该正方体的截面,使得该截面与平面平行,写出作法,并说明理由;
【答案】答案见解析
【分析】利用线面平行的判定定理、面面平行的判定定理即可求解.
【详解】取的中点H,
连接,截面为要求作的截面.
理由如下:
因为E,F分别为的中点,所以,
又平面平面,所以平面.
在正方形中,因为G为的中点,
所以,且,
所以四边形为平行四边形,
所以,同理可证,
又平面平面,
可得平面.
又,平面,
所以平面平面.
连接,因为G为的中点, H为中点,
所以,
又,则,
所以,B,H,G四点共面,
从而截面为要求作的截面.
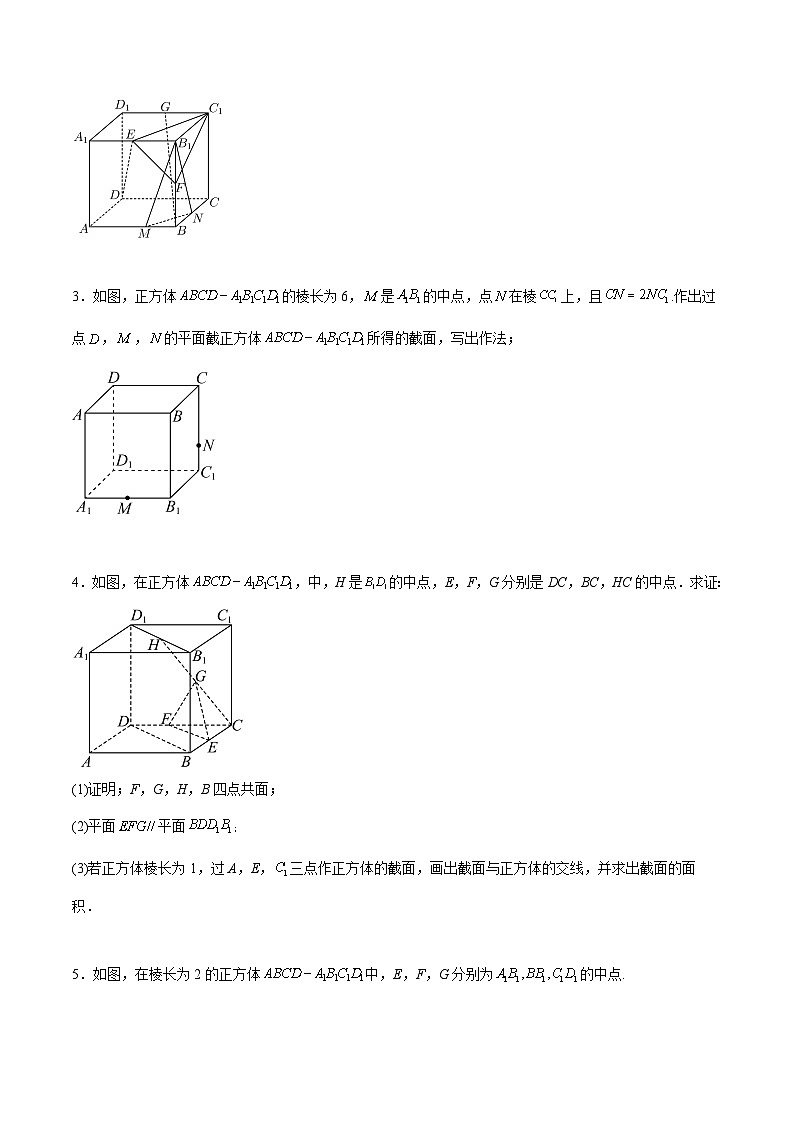
3.如图,正方体的棱长为6,是的中点,点在棱上,且.作出过点,,的平面截正方体所得的截面,写出作法;
【答案】答案见解析
【分析】由平面的基本性质作图.
【详解】如图所示,五边形即为所求截面.
作法如下:连接并延长交的延长线于点,
连接交于点,交的延长线于点,
连接交于点,连接,,
所以五边形即为所求截面.
4.如图,在正方体,中,H是的中点,E,F,G分别是DC,BC,HC的中点.求证:
(1)证明;F,G,H,B四点共面;
(2)平面平面﹔
(3)若正方体棱长为1,过A,E,三点作正方体的截面,画出截面与正方体的交线,并求出截面的面积.
【答案】(1)证明见解析
(2)证明见解析
(3)画图见解析,截面的面积为.
【分析】(1)连接BH,可得,即可证明F,G,H,B四点共面;
(2)由面面平行的判定定理即可证明;
(3)取的中点N,连接,,取的中点M,连接,,画出截面,求解即可.
【详解】(1)证明:连接BH,∵FG为的中位线,
∴,∴F,G,H,B四点共面;
(2)由(1)知,,
∵平面,平面,∴平面;
∵,平面,平面,∴平面,
∵,EF、EG都在面EFG内,∴平面平面
(3)取的中点N,连接,,∴,,
取的中点M,连接,,∴,,
∴截面为平行四边形,且,
所以截面的面积为.
5.如图,在棱长为2的正方体中,E,F,G分别为的中点.
(1)过作该正方体的截面,使得该截面与平面平行,写出作法,并说明理由;
(2)设分别为棱上一点,与均不重合,且,求三棱锥体积的最大值.
【答案】(1)答案见解析
(2)
【分析】(1)取的中点H,连接,所以截面为要求作的截面.通过面面平行的判定进行证明;
(2)利用三棱锥的体积公式并结合均值不等式进行求解.
【详解】(1)取的中点H,
连接,所以截面为要求作的截面.
理由如下:
因为E,F分别为的中点,所以,又平面平面,所以平面.
在正方形中,因为G为的中点,所以,且,
所以四边形为平行四边形,所以,同理可证,
又平面平面,可得平面.
又,平面,所以平面平面.
连接,因为G为的中点, H为中点,所以,又,则,
所以,B,H,G四点共面,从而截面为要求作的截面.
(2)设,由,
得,则,
当仅当时,等号成立.
,
因为,所以三棱琟体积的最大值为.
2.截面的周长及面积问题
6.如图,在棱长为1的正方体中,分别为棱的中点,过作该正方体外接球的截面,所得截面的面积的最小值为( )
A.B.C.D.
【答案】C
【分析】易得正方体外接球的球心在其中心点处,要使过的平面截该球得到的截面面积最小,则截面圆的圆心为线段的中点求解.
【详解】解:如图,
正方体外接球的球心在其中心点处,球的半径,
要使过的平面截该球得到的截面面积最小,则截面圆的圆心为线段的中点,
连接,则,
所以,
此时截面圆的半径,
此时,截面面积的最小值.
故选:C.
7.已知正方体的棱长为2,点为线段的中点,若点平面,且平面,则平面截正方体所得截面的周长为( )
A.B.C.D.
【答案】C
【分析】记的中点分别为E,F,先证三角形即为平面截正方体所得截面,然后可得周长.
【详解】记的中点分别为E,F,连接,
由正方体性质可知,平面,
因为平面,所以
又为正方形,所以
因为,平面,所以平面,
因为平面,所以
因为P,E分别为的中点,所以,所以,
同理可证,
又,平面
所以平面,
所以三角形即为平面截正方体所得截面,
易知三角形为正三角形,
所以截面周长为.
故选:C
8.在棱长为2的正方体中,P,Q是,的中点,过点A作平面,使得平面平面,则平面截正方体所得截面的面积是( )
A.B.2C.D.
【答案】C
【分析】取中点,中点,利用面面平行的判定定理确定平面,利用余弦定理及三角形面积公式求解即可.
【详解】如图,取中点,中点,连接,
因为,平面,平面,所以平面,
又,平面,平面,所以平面,又,
平面,平面,所以平面平面,
即三角形为所得截面,
在中,,,
由余弦定理得,
所以,
所以.
故选:C.
9.如图,在棱长为4的正方体中,的中点是P,过点作与截面平行的截面,则该截面的周长为( )
A.B.C.D.4
【答案】C
【分析】分别取的中点,可得四边形为平行四边形,即为过点的截面,求出其周长可得答案.
【详解】分别取的中点,连接,
可得,可得四边形为平行四边形,可得,
因为,所以四边形为平行四边形,可得,
所以,所以四边形为平行四边形,,
平面即为过点的截面,
平面,平面,所以平面,
因为,所以四边形为平行四边形,可得,
平面,平面,所以平面,
且,平面,所以平面平面,
,,
所以截面的周长为.
故选:C.
10.在《九章算术》中,底面是直角三角形的直三棱柱被称为“堑堵”,如图,棱柱为一“堑堵”,是的中点,,则在过点且与直线平行的截面中,当截面图形为等腰梯形时,该截面的面积等于 ,该“堑堵”的外接球的表面积为 .
【答案】
【分析】取中点,利用线线平行可得线面平行,进而可得四边形即为符合要求的等腰梯形.即可由长度关系确定、、均为等边三角形.由三角形面积即可求解空1,补形为正方体,即可由正方体的外接球求解.
【详解】如图,分别取的中点E,F,G,连接FG,EP,EF,,
则且.在直三棱柱中,易知且,
∵E,P分别为的中点,且,
∴四边形为平行四边形,且,
,目,四点共面.
∵E,F分别为的中点,,又平面,平面,
平面.
,且F,G分别为的中点,,
,
∴四边形即为符合要求的等腰梯形.
当不是的中点时,不平行于平面,
则四边形不是等腰梯形,故等腰梯形有且仅有一个.
取的中点,连接DF、DG,
∵,,且点为的中点,∴且 ,
∴四边形为平行四边形,可得,同理可得,
、、均为等边三角形.
.
将三棱柱补成正方体,
则其外接球即为正方体的外接球,故正方体的体对角线为外接球的一条直径,
∴外接球的直径,
故球的表面积为.
故答案为:,
11.在正三棱柱中,,,,,平面CMN截三棱柱所得截面的周长是( )
A.B.
C.D.
【答案】B
【分析】首先作出截面,再根据几何关系求边长,即可求解周长.
【详解】如图1,延长与交于点,连结,与交于点,
连结,则四边形为所求截面,
其中,,
如图2,,所以,即,
如图1,若,则,所以,
即点是的中点,
所以,
中,,
所以,
所以四边形的周长为.
故选:B
3.截面分体积
12.在斜三棱柱中,,分别为侧棱,上的点,且知,过,,的截面将三棱柱分成上下两个部分体积之比为( )
A.B.C.D.
【答案】A
【分析】由已知中三棱柱的侧棱和上各有一动点,满足,可得四边形与四边形的面积相等,等于侧面的面积的一半,根据等底同高的棱锥体积相等,可将四棱锥的体积转化三棱锥的体积,进而根据同底同高的棱锥体积为棱柱的,求出四棱锥的体积,进而得到答案.
【详解】设三棱柱的体积为
侧棱和上各有一动点,满足,
四边形与四边形的面积相等.
故四棱锥的体积等于三棱锥的体积等于.
则四棱锥的体积等于.
故过,,三点的截面把棱柱分成两部分,则其体积比为
故选:.
13.如图,正方体,中,E、F分别是棱AB、BC的中点,过点、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为,记,则 .
【答案】
【分析】根据平面的基本性质画出过的截面,再利用柱体、锥体的体积公式求,即可得结果.
【详解】延长交的延长线与点,连接交于点,连接:
延长交的延长线与点,连接交于点,连接:
所以过的截面为,如下图示:
设正方体的棱长为,
则过的截面下方几何体的体积为,
所以另一部分体积为,则.
故答案为:
14.如图,在长方体中,.分别过的两个平行截面将长方体分成三部分,其体积分别记为,若,则截面的面积为( )
A.B.C.D.16
【答案】C
【分析】由体积比求出的长,则,进而即可得到截面的面积.
【详解】因为长方体平面平面,
平面平面,平面平面,
所以,同理可得,
所以,,,
所以,
又因为,所以,
所以,
因为平面,平面,所以,
所以,
故选:C.
15.如图,正方体中,点,,分别是,的中点,过点,,的截面将正方体分割成两个部分,记这两个部分的体积分别为,则( )
A.B.C.D.
【答案】C
【分析】如图所示,过点,,的截面下方几何体转化为一个大的三棱锥,减去两个小的三棱锥,上方部分,用总的正方体的体积减去下方的部分体积即可.
【详解】作直线,分别交于两点,连接分别交于两点,
如图所示, 过点,,的截面即为五边形 ,
设正方体的棱长为,
因为点,,分别是,的中点
所以,即,
因为,
所以
则过点,,的截面下方体积为:,
∴另一部分体积为,
∴.
故选:C.
16.在棱长为a的正方体中,E,F分别为棱BC,的中点,过点A,E,F作一个截面,该截面将正方体分成两个多面体,则体积较小的多面体的体积为 .
【答案】
【分析】先作出截面,判断出为三棱台,结合台体体积公式运算求解.
【详解】如图,依次连接,四边形即为所求截面,
因为点E、F分别为棱、的中点,所以∥,
可知为三棱台,所以,
其体积,
且正方体的体积为,
则另一部分的体积为,
因为,所以体积较小的多面体的体积为.
故答案为:.
17.如图所示,已知平行六面体,E是中点,过的截面把平行六面体分成两个部分,求左右两部分体积之比.
【答案】7:17
【分析】被截面分割成的左边的几何体是个三棱台,要求其体积,由于E为中点,可补成锥体,也即补上一个全等的平行六面体就能迅速求解.
【详解】
的延长线交延长线于,由E为中点知A为中点,联结,则和的交点必在F.作,,,即补上一个全等的平行六面体.
,
,
.
又
,.
4.球截面问题
18.在三棱锥中,和都是等边三角形,,平面平面,M是棱AC上一点,且,则过M的平面截三棱锥外接球所得截面面积的最大值与最小值之和为( )
A.24πB.25πC.26πD.27π
【答案】D
【分析】根据题设找到三棱锥外接球球心位置,由已知及球体截面的性质求过M平面截球体的最大截面积,根据外接球球心、面面垂直以及比例关系易知共线,且过M平面截球体的最小截面积时该平面,且,即可求最大、最小面积和.
【详解】由题设,若为中点,分别是等边和等边的中心,
连接,则分别在上,且,
,,,面,故面,
又面,所以,面面,
又面面,过作面的垂线与过作面的垂线交于,
即面,面,则为外接球球心,
面,且,,则面,所以面面,
综上,结合面面,面面,则面、面为同一平面,所以面,
由面面,,面,面面,
所以面,面,即,且知:为正方形,
如图,
,,若外接球半径为,
所以,
由球体的性质,要使过M平面截三棱锥外接球所得截面面积的最大,则平面必过球心,
所以,最大截面圆面积为,
要使过M平面截三棱锥外接球所得截面面积的最小,则该平面,
因为,而都在面上,故,
而,故,显然共线,故,
此时截面圆的半径为,则,
所以,最小截面圆面积为,
综上,最大值与最小值之和为.
故选:D.
【点睛】关键点点睛:根据球的性质判断过M平面截棱锥外接球截面面积最大、最小时截面与的位置关系,利用几何关系求截面圆半径,最后求面积和.
19.已知正四面体ABCD的表面积为,E为棱AB的中点,球О为该正四面体的外接球,则过DE的平面被球О所截得的截面面积最小值为( )
A.B.C.D.
【答案】C
【分析】先根据表面积求出四面体的棱长,得出外接球的半径,根据截面圆的性质可得答案.
【详解】设正四面体的棱长为,则,∴,
∴正四面体的高为;
将正四面体放置于正方体中,如图1所示:可得正方体的外接球就是正四面体的外接球,
∵正四面体的棱长为2,∴正方体的棱长为,可得外接球半径满足,
E为棱AB的中点,过DE作其外接球的截面,当球心O到截面的距离最大时,截面圆的面积达到最小值,
此时球心O到截面的距离等于O到DE的距离,O到DE的距离为,
可得截面圆的半径为,得到截面圆的面积最小值为.
故选:C.
20.在矩形中,,将沿对角线翻折至的位置,使得平面平面,则在三棱锥的外接球中,以为直径的截面到球心的距离为( )
A.B.C.D.
【答案】B
【分析】如图,取的中点为,连接,过作,垂足为,连接,可证为三棱锥的外接球的球心,利用解直角三角形可求,据此可求球心到以为直径的截面的距离.
【详解】如图,取的中点为,连接,过作,垂足为,连接.
因为三角形为直角三角形,故,
同理,故,
所以为三棱锥的外接球的球心,而,
因为,平面,平面平面,
平面平面,故平面,
而平面,故.
在直角三角形中,,故,
故,
在直角三角形中,,
故,故.
设球心到以为直径的截面的距离为,
则,
故选:B.
【点睛】思路点睛:三棱锥外接球的球心,可根据球心的定义来判断(即球心到各顶点的距离相等),而球面截面圆的半径、球心到截面的距离、球的半径可构成直角三角形.
21.已知三棱锥满足底面,在中,,,,是线段上一点,且,球为三棱锥的外接球,过点作球的截面,若所得截面圆的面积的最小值与最大值之和为,则球的表面积为( )
A.72πB.86πC.112πD.128π
【答案】D
【分析】先找到外接球球心,过的中点作,则平面,取,则为外接球球心,过点作球的截面,最大的截面过球心,最小的截面是过且与垂直的截面,由此可用表示出两截面圆半径.
【详解】如图,是边中点,是边中点,∵,∴是的外心,
作,∵平面,∴平面,平面,
∴,取,易得,
∴是三棱锥的外接球的球心.
是中点,则,,∴,
∵,∴,∴,
设,则,,又,
∴,
过且与垂直的截面圆半径为,则,
这是最小的截面圆半径,最大的截面圆半径等于球半径,
∴,,
,.
故选:D.
22.如图,已知正四棱锥的所有棱长均为4,平面经过,则平面截正四棱锥的外接球所得截面圆的面积的最小值为( )
A.B.C.D.
【答案】C
【分析】连接、交于,连接,求出,,可得点即为正四棱锥的外接球球心,取中点,连接,当时,截面圆的面积最小,线段也即此时截面圆的直径,求出截面圆的面积即可.
【详解】连接,交于,连接,则底面且是中点,
,,
所以到,,,,的距离均为,点即为正四棱锥的外接球球心,取中点,连接,分析可知,当时,截面圆的面积最小,线段也即此时截面圆的直径,所以截面圆的面积的最小值为.
故选:C.
23.已知三棱锥中,Q为BC中点,,侧面底面,则过点Q的平面截该三棱锥外接球所得截面面积的取值范围为 .
【答案】
【分析】连接,找到球心到平面和平面的射影为和的中心,,再通过面面垂直的性质定理和线面垂直的性质定理得到,再利用勾股定理求出相关长度,找到截面圆的最值情况,代入计算即可得到答案.
【详解】连接,由,
可知:和是等边三角形,
设三棱锥外接球的球心为,
所以球心到平面和平面的射影是和的中心,,
是等边三角形,为中点,所以,
又因为侧面底面,侧面底面,侧面,
所以底面,而底面,因此,
所以是矩形,应为和是边长为4的等边三角形,
所以两个等边三角形的高,
在矩形中,,
连接,所以,
设过点的平面为,当时,此时所得截面的面积最小,该截面为圆形,
可得,
因此圆的半径为,
所以此时面积为,当点在以为圆心的大圆上时,此时截面的面积最大,
面积为:,所以截面的面积范围为.
故答案为:.
5.求截面图形的个数
24.过正四面体的顶点P作平面,若与直线,,所成角都相等,则这样的平面的个数为( )个
A.3B.4C.5D.6
【答案】B
【分析】如图补全四棱柱,易得平面与直线,,所成角都相等,即可得一个平面,说明,,与平面所成的角相等,同理可得直线,,与平面、平面所成角都相等,从而可得出答案.
【详解】解:如图,将正四面体看成四棱柱的左下角一部分,
由正四面体可知,
平面与直线,,所成角都相等,
故过点P做平面平面,
则此时的平面与直线,,所成角都相等,
因为,
则与平面所成的角相等,
又因,
所以直线,,与平面所成的角相等,
故过点P做平面平面,
则此时的平面与直线,,所成角都相等,
同理,直线,,与平面、平面所成角都相等,
即平面平面时,平面与直线,,所成角都相等,
平面平面时,平面与直线,,所成角都相等,
综上所述,这样的平面的个数为4个.
故选:B.
25.正方体中与的交点称为正方体的中心,平面经过点,且顶点,到平面的距离相等,则这样的平面的个数为( )
A.1B.2C.0D.无数个
【答案】D
【分析】取正方体各条棱的中点并连接,形成三个过点的平面,显然这三个平面是符合题意的平面,根据排除法可知,选项D正确.
【详解】
由题意得,取正方体各条棱的中点并连接,如图,形成三个过点的平面,显然这三个平面是符合题意的平面,根据排除法可知,选项D正确.
故选:D.
26.设四棱锥的底面不是平行四边形, 用平面去截此四棱锥,使得截面四边形是平行四边形,则这样的平面
A.有无数多个B.恰有个C.只有个D.不存在
【答案】A
【详解】
如图由题知面与面相交,面与面相交,可设两组相交平面的交线分别为,由决定的平面为,作与且与四条侧棱相交,交点分别则由面面平行的性质定理得:从而得截面必为平行四边形.由于平面可以上下平移,可知满足条件平面有无数多个.故本题答案选.
27.用一个平面去截正四面体,使它成为形状、大小都相同的两个几何体,则这样的平面的个数为 .
【答案】9.
【分析】根据正四面体的结构特征,分别取各条棱的中点,利用相交直线确定的平面,即可求解.
【详解】由题意,如图所示,设三棱锥的各条棱长都相等,
取的中点,分别连接,
则两相交直线所确定的平面可把正四面体分成形状、大小都相同的两个几何体,
同理分别取各条棱的中点,可构成6个这样的平面,满足题意,
所以这样的平面的个数为6个.
还有过AB,AC,SB,SC的中点构成的平行四边形所在平面,可把正四面体分成形状、大小都相同的两个几何体,
类似这种共有3个.
所以共有9个
【点睛】本题主要考查了空间几何体的结构特征,其中解答中确定正四面体性质和结构特征是解答的关键,着重考查了空间想象能力,属于基础题.
6.截面的最值问题
28.在三棱锥中,,平面经过的中点E,并且与BC垂直,当α截此三棱锥所得的截面面积最大时,此时三棱锥的外接球的表面积为( )
A.B.C.D.
【答案】D
【分析】取靠近的四等分点,的中点,截此三棱锥所得的截面为平面,当时截面面积最大,,为,外接圆圆心,球心满足面,面,由求得外接球的半径进而求得球的表面积.
【详解】
如图所示,取中点及靠近的四等分点,的中点,连接,,,,,
由,所以,又是中点,是的中点,所以
可知,同理可得,
又,平面,平面,所以平面,所以平面即为平面,
又因为,所以,所以,
所以截此三棱锥所得的截面面积为,
当时,取得最大值,
设外接球球心为,半径为,,分别为,外接圆圆心,球心满足面,面,
又因为和均为边长为4的正三角形,所以,
所以四边形为正方形,且,又,所以,
∴.
故选:D.
29.在正方体中,平面经过点B、D,平面经过点A、,当平面分别截正方体所得截面面积最大时,平面所成的锐二面角大小为( )
A.B.C.D.
【答案】C
【分析】设平面与面所成的二面角为,二面角为,分和两种情况讨论,证明平面经过点B、D且截正方体所得截面面积最大时,平面与面重合,从而可得出答案.
【详解】平面经过点B、D且截正方体所得截面面积最大时,平面与面重合,
证明:设平面与面所成的二面角为,二面角为,
当时,记平面截正方体所得截面为面,,
则,
令,
因为,所以,
当时,显然平面截正方体所得截面面积最大时,
截面为面,
当时,平面截正方体所得截面为,
所以平面截正方体所得截面面积最大时截面为面,
同理平面过时,截正方体所得截面面积最大时截面为面,
连接,面与面所成锐二面角为,
因为面面,
所以的所成角大小为二面角大小,
因为,所以面与面所成锐二面角大小为.
故选:C.
【点睛】关键点点睛:解决本题的关键在于说明平面经过点B、D且截正方体所得截面面积最大时,平面与面重合,考查了分类讨论思想和极限思想.
30.已知圆锥的侧面积为20π,底面圆O的直径为8,当过圆锥顶点的平面截该圆锥所得的截面面积最大时,则点O到截面的距离为 .
【答案】
【分析】由题可得圆锥的高,母线长,可得过圆锥顶点的平面截该圆锥所得的截面为直角三角形时面积最大,再利用等体积法即求.
【详解】设圆锥的底面圆的半径为r,高为h,母线长为l,则,
∴,h=3,
由于h
,
∴,即,
∴,即点O到截面的距离为.
故答案为:.
31.如图,在棱长都等于1的三棱锥中,是上的一点,过作平行于棱和棱的截面,分别交,,于,,.
(1)证明截面是矩形;
(2)在的什么位置时,截面面积最大,说明理由.
【答案】(1)证明见解析
(2)是的中点时,截面面积最大
【分析】(1)先证明四边形是平行四边形,然后证明平行四边形是矩形.
(2)求得截面面积的表达式,并利用二次函数的性质求得其取最大值时的位置.
【详解】(1)平面,平面平面,平面,
,同理,
,同理,
四边形是平行四边形,
取中点,连接,,
,是中点,
,同理,
又,平面,平面,
平面,,
又,,,即四边形是矩形.
(2)设,,由(1)知,
又,,
则,
当时,最大,即是的中点时,截面面积最大.
32.如图,空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于点E,F,G,H.E在AB的何处时截面EGFH的面积最大?最大面积是多少?
【答案】E为AB的中点,a2.
【分析】设AE∶AB=x,利用平行四边形的面积公式可得面积的表达式,再根据二次函数的性质可求面积的最大值.
【详解】因为平面,平面,平面平面,
所以,同理,故,同理.
所以四边形为平行四边形.
∵AD与BC成60°角,∴∠HGF=60°或120°.
设AE∶AB=x,则=x.
又BC=a,∴EF=ax.由=1-x,得EH=a(1-x).
∴四边形的面积为EF×EH×sin 60°=ax×a(1-x)×a2(-x2+x)
=a2.
当x=时,即当E为AB的中点时,截面的面积最大,最大面积为a2.
1.如图所示,在长方体中,用截面截下一个棱锥则棱锥的体积与剩余部分的体积之比为( )
A.1:5B.1:4C.1:3D.1:2
【答案】A
【分析】由长方体的性质,结合三棱锥的体积公式、长方体的体积公式求及剩余部分的体积,进而求其比例即可.
【详解】由图知:,,而,
∴剩余部分的体积为,
∴棱锥的体积与剩余部分的体积之比为1:5.
故选:A
2.已知正四面体的体积为,为棱的中点,球为该正四面体的外接球,则过点的平面被球所截得的截面面积的最小值为( )
A.B.C.D.
【答案】B
【分析】根据题意,根据正四面体的体积求出棱长和正方体的边长,再利用正方体的体对角线等于外接球的直径,即可求出球的半径,当过点的截面到球心的距离最大为时,截面圆的面积达最小值,最后利用球的截面的性质求出截面圆的半径,即可求出截面圆的面积最小值.
【详解】如图所示,球为正四面体的外接球,即为正方体的外接球,
正四面体的体积为,
设正四面体的棱长为,则正方体的棱长为,
所以,解得,
设正四面体的外接球的半径为,则,
基底,
因为为棱的中点,过点作其外接球的截面,
当截面到球心的距离最大值时,截面圆的面积达最小值,
此时球心到截面距离等于正方体棱长的一半,即,
可得截面圆的半径为:,
所以截面圆的面积最小值为:.
故选:B.
3.已知直四棱柱的底面为正方形,,为的中点,过三点作平面,则该四棱柱的外接球被平面截得的截面圆的周长为( )
A.B.C.D.
【答案】D
【分析】先根据题意得到该四棱柱的外接球球心的位置与半径,再求得平面即为平面,再利用线面平行的性质与线面垂直的判定定理求得球心到平面的距离,从而得解.
【详解】由题意知直四棱柱的外接球的半径,
如图,取的中点,连接,易知四边形为矩形,且平面即为平面,
分别取的中点,连接,则易得四边形为正方形,
由四棱柱的对称性可知,其外接球的球心即为正方形的中心,取的中点,连接,
则平面,平面,所以平面,故球心到平面的距离与到平面的距离相等,
过点作,垂足为,
易知面,面,故,
又平面,所以平面,
又,所以球心到平面的距离为,
由球的性质知,截面圆的半径,
所以截面圆的周长为.
故选:D.
【点睛】关键点睛:本题的关键是求得球心到面的距离,从而求得截面圆的半径即可得解.
4.在三棱锥中,两两垂直,且,半径为1的球在该三棱锥内部且与面、面、面均相切.若平面与球相切,则三棱锥的外接球被平面所截得的截面面积的最小值为( )
A.B.C.D.
【答案】C
【分析】先推出球的截面面积与球心距离的关系,再根据条件将三棱锥看作正方体的一部分,求出外接球的球心和半径,运用前面推出的关系求解.
【详解】设截面圆与球心的距离为h,球的半径为R,截面圆的半径为r,则,
即h越大,截面的面积越小;
由题意三棱锥是正方体的一部分,
其外接球的球心为正方体对角线AH的中点,
外接球的半径,则,如下图:
以BC为x轴,BD为y轴,BA为z轴建立坐标系,则,,
到球O球面上最远的点距离为,
此时以最远点为切点的平面截外接球截面圆的半径为,
即截面面积的最小值为;
故选:C.
5.中国正在由“制造大国”向“制造强国”迈进,企业不仅仅需要大批技术过硬的技术工人,更需要努力培育工人们执著专注、精益求精、一丝不苟、追求卓越的工匠精神.这是传统工艺革新技术的重要基石.如图所示的一块木料中,四边形是正方形,.
(1)要经过点将木料锯开,使得截面平行于侧棱,在木料表面应该怎样画线,请说明理由并计算截面面积.
(2)已知点是侧棱上的动点,要经过点将木头锯开,使得截面垂直于侧棱且截面面积最大,在木料表面应该怎样画线,请说明理由并计算截面面积.
【答案】(1)的中点与点相连,理由见解析,截面面积为;
(2)顺次连接上靠近的三等分点,上靠近的三等分点,上靠近的三等分点,理由见解析,最大面积
【分析】(1)取的中点,利用线面平行的判定推理,求出截面面积作答.
(2)根据给定条件,证明平面,再利用面面平行确定截面与棱的交点位置,求出截面面积的函数关系,求出最大值作答.
【详解】(1)取的中点,连接,于是即为所画线.
连接,连接,由四边形是正方形,得为的中点,
则有,而平面,平面,因此平面,
所以是所作截面,由,得,
显然都是正三角形,有,则,所以截面面积.
(2)由(1)知,,而,平面,则平面,
因此过点垂直于的截面与截面平行或重合,
显然点在上(不含端点)时,截面面积小于,不可能最大,
当点在上(不含端点)时,令,此时截面交分别于点,
平面平面,平面平面,平面平面,
因此,同理,由平面,平面,
得平面,而平面平面,平面,则,同理,
于是,四边形为平行四边形,又,则,
即有,为矩形,
显然,则,,,
由,得,而,矩形面积,
从而截面的面积,
当时,,显然,于是当时,截面面积最大,
所以点是上靠近的三等分点,再与上靠近的三等分点,上靠近的三等分点,
顺次连接的线段即为所画线,此时截面面积最大,最大值为.
【点睛】方法点睛:作截面的常用三种方法:直接法,截面的定点在几何体的棱上;平行线法,截面与几何体的两个平行平面相交,或者截面上有一条直线与几何体的某个面平行;延长交线得交点,截面上的点中至少有两个点在几何体的同一平面上.
6.直三棱柱中,,P为BC中点,,Q为上一点,,则经过A,P,Q三点的平面截此三棱柱所成截面的面积是( )
A.B.4C.D.5
【答案】C
【分析】如图,在上取点M,使得,取的中点N,连接,则,利用线面垂直的判定定理与性质可得,则截面为直角梯形APQM,结合题意求出QM、AP、PM,由梯形的面积公式计算即可求解.
【详解】如图,在上取点M,使得,取的中点N,连接,
则,又,所以,
得A、P、M、Q四点共面,又,为BC的中点,所以,
由,得,又平面,
所以平面,由平面,得,
所以截面为直角梯形APQM,且,得,
所以,
作于D,则,
所以.
故选:C.
7.如图,直三棱柱,,,侧棱长为,点是侧面内一点.当最大时,过、、三点的截面面积的最小值为 .
【答案】3
【分析】设由余弦定理结合均值不等式可得当且仅当时,取得最大值,得到此时三棱柱是正三棱柱,过点作,连接,可得过、、三点的截面即为平面,由,求出最小值,即可得到答案.
【详解】在中,设,,,
由余弦定理可得:,
即,即,
由,则(当且仅当时等号成立),
所以,
所以即(当且仅当时等号成立),
即当时,取得最大值4.此时三棱柱是正三棱柱,
过点作,则,连接,
过、、三点的截面即为平面.,
由三棱柱为直三棱柱,则平面,
所以,由,则,
所以四边形为矩形,则,
当最小时,最小.
当平面时,即,最小. 此时,
所以最小值为,
故答案为:3.
8.空间给定不共面的A,B,C,D四个点,其中任意两点间的距离都不相同,考虑具有如下性质的平面:A,B,C,D中有三个点到的距离相同,另一个点到的距离是前三个点到的距离的2倍,这样的平面的个数是___________个
【答案】32
【分析】按照四个点的位置不同分类讨论,即可求解
【详解】首先取3个点相等,不相等的那个点由4种取法;
然后分3分个点到平面的距离相等,有以下两种可能性:
(1)全同侧,这样的平面有2个;
(2)不同侧,必然2个点在一侧,另一个点在一侧,
1个点的取法有3种,并且平面过三角形两个点边上的中位线,
考虑不相等的点与单侧点是否同侧有两种可能,每种情况下都唯一确定一个平面,
故共有6个,
所有这两种情况共有8个,综上满足条件的这样的平面共有个,
故答案为:32
9.过正四面体ABCD的顶点A作一个形状为等腰三角形的截面,且使截面与底面BCD所成的角为,这样的截面有( )
A.6个B.12个C.16个D.18个
【答案】D
【分析】根据ABCD是正四面体和过点A的截面是等腰三角形,分,,讨论求解.
【详解】如图,在正四面体ABCD中,因为过点A的截面是等腰三角形,
若,则截面与底面BCD所成的角为有如下情形,
如图所示:
在高线的两侧的截面、截面与底面BCD所成的角为(,与BC平行),
同理截面的一边与CD平行也有2个,与BD平行也有2个,共有6个.
若,同理也有6个;
若,同理也有6个.
综上所述,满足题意的截面共有18个,
故选:D.
【点睛】本题主要考查几何体的结构特征以及平面与平面的位置关系,还考查了分类讨论的思想和分析问题的能力,属于中档题.
10.如图,在直三棱柱中,,,,,为线段上的一动点,则过三点的平面截该三棱柱所得截面的最小周长为 .
【答案】/
【分析】利用直三棱柱的侧面展开图求解即可.
【详解】由题意可知过三点的平面截该三棱柱所得截面的周长即的周长,
因为直三棱柱,所以各侧面均为矩形,
所以,
直三棱柱的侧面部分展开图如图所示,
则在矩形中,
所以过三点的平面截该三棱柱所得截面的最小周长为,
故答案为:
11.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面为直角梯形,CD//AB,AD⊥AB,且PA=AD=CD=2,AB=3,E为PD的中点.
(1)证明:AE⊥平面PCD;
(2)过A,B,E作四棱锥P﹣ABCD的截面,请写出作法和理由,并求截面的面积.
【答案】(1)证明见解析
(2)作法和理由见解析,
【分析】(1)由结合线面垂直的判定证明即可;
(2)作EF//CD,得出EF//AB,从而得出截面,再由梯形的面积公式得出截面面积.
【详解】(1)证明:因为PA⊥平面ABCD,所以CD⊥PA.
又CD//AB,AD⊥AB,所以CD⊥AD.
因为AD∩PA=A,所以CD⊥平面PAD,则CD⊥AE.
因为PA=AD,E为PD的中点,所以AE⊥PD.又CD∩PD=D,所以AE⊥平面PCD.
(2)解:如图,过E作EF//CD,交PC于F,连接BF,则截面为四边形ABFE.
理由如下:
因为AB//CD,EF//CD,所以EF//AB,所以A,B,F,E四点共面,从而过A,B,E的截面为四边形ABFE.
由(1)知AE⊥平面PCD,所以AE⊥EF,
又,,AB=3,
所以四边形ABFE为直角梯形,其面积.
12.矩形ABCD中,(如图1),将沿AC折到的位置,点在平面ABC上的射影E在AB边上,连结(如图2).
(1)证明:;
(2)过的平面与BC平行,作出该平面截三棱锥所得截面(不要求写作法).记截面分三棱锥所得两部分的体积分别为,求.
【答案】(1)证明见解析
(2).
【分析】(1)利用线面垂直的性质定理证明线线垂直;
(2)根据三角形的等面积法求出的长度,再根据勾股定理求出长度,进而确定,即可确定所求截面,利用椎体体积公式求解.
【详解】(1)因为平面,平面,所以,
且由翻折关系可知,
且,平面,
所以平面,
又因为平面,所以.
(2)由(1)可知,平面,
又因为平面,所以.
且,
所以,
且,所以,所以,
所以,解得,
所以,所以,
所以取的三等分点为,且,
连接,
则有,平面,平面,
所以平面,所以所作截面为平面,
因为的相似比为,
所以,所以,
所以.
13.在三棱锥S—ABC中,△ABC是边长为2的等边三角形,∠SCA=90°,D为SA的中点,SC=BD=2.
(1)如图,过BD画出三棱锥S—ABC的一个截面,使得这个截面与侧面SAC垂直,并进行证明;
(2)求(1)中的截面将三棱锥S—ABC分割成两个棱锥的体积之比.
【答案】(1)答案见解析
(2)1:3
【分析】(1)取的中点,连接BE、DE,则即为所作的截面,由可得,又,即可得到平面,从而得证.
(2)依题意利用勾股定理逆定理可得,由面面垂直的性质得到平面,再分别根据、求出几何体的体积,即可得解;
(1)
解:取的中点,连接BE、DE,则即为所作的截面,如图所示.
下面证明:因为是的中位线,所以,
又,所以.
因为是等边三角形,所以.
又,平面,所以平面.
又平面,所以平面平面.
(2)
解:由是的中位线,得;
由是边长为2的等边三角形,得;
又,所以,由勾股定理的逆定理,得,即,
由(1)得平面平面,平面平面,所以平面.
;
,
故截面将三棱锥分割成两个棱锥的体积之比为.
14.在棱长为2的正方体中,平面,则以平面截正方体所得的截面面积最大时的截面为底面,以为顶点的锥体的外接球的表面积为( )
A.B.C.D.
【答案】B
【分析】由正方体的对称性,可知当截面为正六边形时,截面面积最大,再分当球心在棱锥内部时和当球心在棱锥外部时,建立方程求得外接球的半径可得选项.
【详解】解:如图,
由正方体的对称性,可知当截面为正六边形时,截面面积最大,
此时正六边形的边长为,
设交截面于,则为的中点,所以,
设正六棱锥外接球的球心为,外接球半径为,
当球心在棱锥内部时,有,解得,
外接球面积为;
若球心在棱锥外部时,有,解得(舍去).
∴以为顶点的锥体的外接球的表面积为.
故选:B.
【点睛】方法点睛:求解几何体外接球半径的思路是依据球的截面的性质:利用球的半径、截面圆的半径及球心到截面的距离三者的关系求解,其中确定球心的位置是关键.
专题突破卷21 立体几何的轨迹问题-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份专题突破卷21 立体几何的轨迹问题-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含专题突破卷21立体几何的轨迹问题原卷版docx、专题突破卷21立体几何的轨迹问题解析版docx等2份试卷配套教学资源,其中试卷共76页, 欢迎下载使用。
专题突破卷17 数列求和-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份专题突破卷17 数列求和-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含专题突破卷17数列求和原卷版docx、专题突破卷17数列求和解析版docx等2份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。
专题突破卷08 极值点偏移-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份专题突破卷08 极值点偏移-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含专题突破卷08极值点偏移原卷版docx、专题突破卷08极值点偏移解析版docx等2份试卷配套教学资源,其中试卷共81页, 欢迎下载使用。












