

2023-2024学年甘肃省兰州五十四中九年级(上)期末数学试卷(含解析)
展开1.9的算术平方根是( )
A. 81B. 3C. −3D. 4
2.从2022年起,某市财政每年将安排50000000元用于建设“美丽乡村”.将数据50000000用科学记数法表示为( )
A. 5×10−7B. 5×107C. 0.5×108D. 50×106
3.在下列各式1a,2xyπ,3abc4,5x+1,x2x+y中,是分式的有( )
A. 2个B. 3个C. 4个D. 5个
4.化简−a 1a的结果是( )
A. aB. − aC. − −aD. −a
5.在Rt△ABC中,∠C=90°,csA=12,那么sinB的值等于( )
A. 12B. 22C. 32D. 1
6.在下列y关于x的函数中,一定是二次函数的是( )
A. y=x2−1B. y=1x2C. y=ax2+bx+cD. y=k2x+3
7.如图,四边形ABCD是某护坡大坝的横截面,AD//BC,坝顶宽AD为5米,斜坡AB的坡度为i=1:3,斜坡CD的坡角为45°,坡长CD=4米,则坝底宽约为( )
A. 16.3米B. 15.8米C. 13.8米D. 11.3米
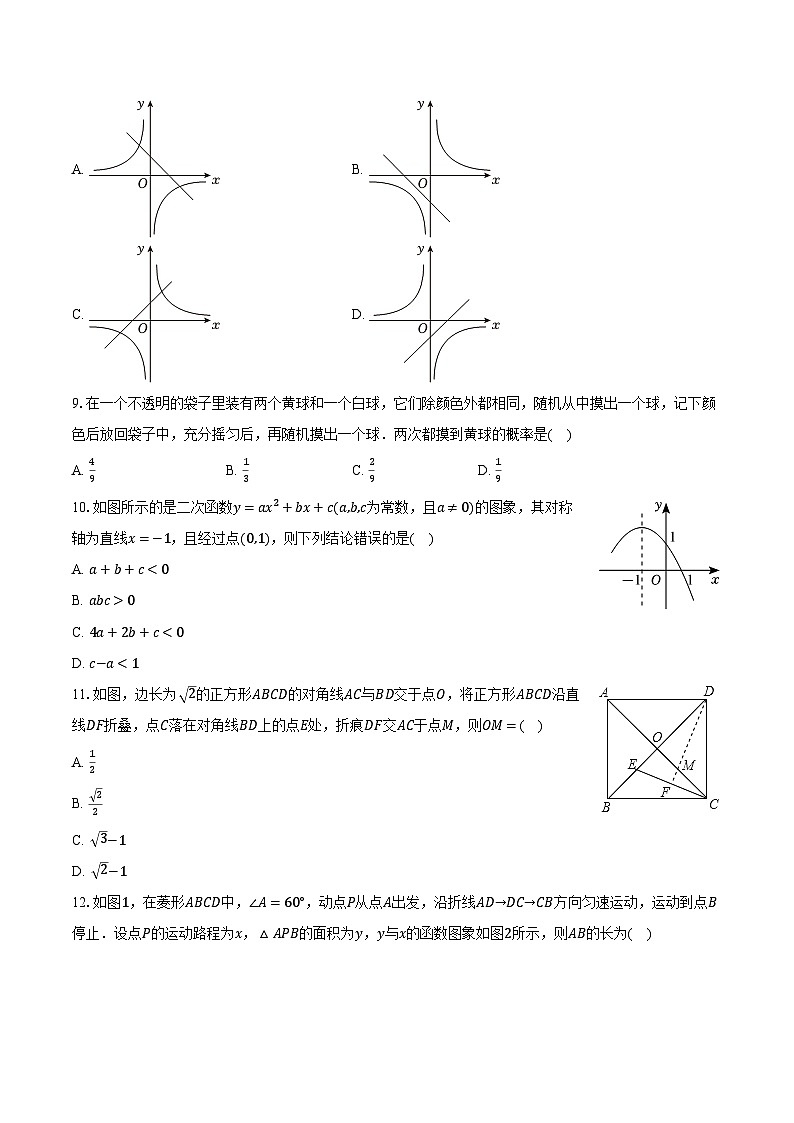
8.一次函数y=ax−a与反比例函数y=ax在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )
A. 49B. 13C. 29D. 19
10.如图所示的是二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象,其对称轴为直线x=−1,且经过点(0,1),则下列结论错误的是( )
A. a+b+c<0
B. abc>0
C. 4a+2b+c<0
D. c−a<1
11.如图,边长为 2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM=( )
A. 12
B. 22
C. 3−1
D. 2−1
12.如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( )
A. 3B. 2 3C. 3 3D. 4 3
二、填空题:本题共4小题,每小题3分,共12分。
13.因式分解:4−a2=______.
14.若a−bb=47,则ab= ______ .
15.若关于x的一元二次方程(k−2)x2−2x+1=0有实数根,则k的取值范围是______ .
16.如图,正方形ABCD的边长是12,E,F,G分别是BC,CD,BD上的点,已知BE=8,DF=9,求三角形EFG周长的最小值______ .
三、解答题:本题共12小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
(1) 12+3 113−23 48;
(2)计算:cs245°−tan30°⋅sin60°.
18.(本小题6分)
(1)计算:2x2+1=3x;
(2)解方程组:x+2y=03x−4y=20.
19.(本小题5分)
如图,AB=DE,BF=EC,∠B=∠E,求证:AC//DF.
20.(本小题6分)
九年级十班的甲、乙两位同学练习百米赛跑:操场上从内道到外道,标有1,2,3,4四个跑道.他们抽签占跑道;
(1)若甲抽到2道,则乙抽到3道的概率是______;
(2)请列表或画树状图求甲、乙在相邻跑道的概率.
21.(本小题6分)
某商场将进货价为30元的台灯以40元售出,平均每月能售出600个,调查表明:售价在40~60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个.为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?
22.(本小题6分)
如图,一次函数y=kx+b与反比例函数y=mx的图象交于A(2,3),B(−3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b
23.(本小题6分)
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,动点P,Q分别从A,C两点同时出发,P点沿边AC向C以每秒3个单位长度的速度运动,Q点沿边BC向B以每秒4个单位长度的速度运动,当P,Q到达终点C,B时,运动停止,设运动时间为t(s).
(1)当运动停止时,t的值为______ ;
(2)设△PCQ的面积为S.
①求S的表达式(用含t的式子表示,并注明t的取值范围);
②求当t为何值时,S取得最大值,这个最大值是多少?
24.(本小题6分)
小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.5米,求路灯杆AB的高度.
25.(本小题6分)
数学活动小组到某景点测量标志性建筑古塔CD的高度,如图,他们在地面上A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,点A、B、C在同一直线上.(身高忽略不计,结果不取近似值)
(1)求证:AB=BD;
(2)求塔CD的高.
26.(本小题6分)
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,点F在AD上,且AF=AB,连接BF交AE于点G,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若BF=10,AB=10,求菱形ABEF的面积.
27.(本小题6分)
已知:二次函数y=x2+bx+c的图象过点A(2,5),C(0,−3).
(1)求此二次函数的解析式;
(2)直接写出当−3≤x≤1时,求y的取值范围.
28.(本小题7分)
已知正方形ABCD,E,F为平面内两点.
【探究建模】
(1)如图1,当点E在边AB上时,DE⊥DF,且B,C,F三点共线.求证:AE=CF;
【类比应用】
(2)如图2,当点E在正方形ABCD外部时,DE⊥DF,AE⊥EF,且E,C,F三点共线.猜想并证明线段AE,CE,DE之间的数量关系;
【拓展迁移】
(3)如图3,当点E在正方形ABCD外部时,AE⊥EC,AE⊥AF,DE⊥BE,且D,F,E三点共线,DE与AB交于G点.若DF=3,AE= 2,求CE的长.
答案和解析
1.【答案】B
【解析】解:9的算术平方根是3,
故选:B.
根据算术平方根的定义即可求出答案.
本题考查算术平方根,解题的关键是熟练运用算术平方根的定义,本题属于基础题型.
2.【答案】B
【解析】解:将数据50000000用科学记数法表示为5×107;
故选:B.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于或等于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
本题主要考查科学记数法,熟练掌握科学记数法是解题的关键.
3.【答案】B
【解析】解:根据分式定义,所给代数式中是分式的有式1a,5x+1,x2x+y,共3个.
故选:B.
分式的定义:如果A、B表示两个整式,并且B中含有字母,那么式子AB叫做分式,据此逐个判断即可.
本题主要考查了分式的判断,熟练掌握分式的定义是解决问题的关键,分母中如果含有字母则是分式,如果不含有字母则不是分式,注意π不是字母,是常数圆周率.
4.【答案】B
【解析】解:∵1a≥0,
∴a≥0,
∴−a≤0,
∴−a 1a=− a,
故选:B.
首先根据二次根式有意义的条件判断a的取值范围,再根据二次根式的性质进行化简即可.
此题主要考查了二次根式的性质与化简,能够正确化简二次根式是解题的关键.
5.【答案】A
【解析】解:∵Rt△ABC中,∠C=90°,csA=12,
∴∠A=60°,
∴∠B=90°−∠A=90°−60°=30°,
∴sinB=sin30°=12.
故选:A.
先根据csA=12求出∠A的度数,再由直角三角形的性质求出∠B的度数,由特殊角的三角函数值即可得出sinB的值.
本题考查的是特殊角的三角函数值及直角三角形的性质,熟记各特殊角的三角函数值是解答此题的关键.
6.【答案】A
【解析】解:A、y=x2−1是二次函数,故此选项符合题意;
B、y=1x2不是二次函数,故此选项不符合题意;
C、y=ax2+bx+c,当a=0时,不是二次函数,故此选项不符合题意;
D、y=k2x+3不是二次函数,故此选项不符合题意.
故选:A.
根据二次函数的定义分别判断即可.
本题主要考查了二次函数的定义,解题的关键是掌握一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.
7.【答案】A
【解析】解:过点A、D作BC的垂线,垂足分别为E、F,
∵AD//BC,
∴四边形AEFD是矩形,
∵斜坡CD的坡角为45°,
∴△DCF是等腰直角三角形,
∵CD=4米,
∴DF=CF=4× 22=2 2,
∴AE=DF=2 2,
∵斜坡AB的坡度为i=1:3,
∴BE=3AE=6 2,
∴BC=BE+EF+CF=8 2+5≈16.3(米).
故选:A.
过点A、D作BC的垂线,垂足分别为E、F,证明四边形AEFD是矩形,△DCF是等腰直角三角形,解直角三角形即可求解.
本题考查解直角三角形的应用,正确地作出辅助线是解题的关键.
8.【答案】A
【解析】解:当a>0时,−a<0,则一次函数y=ax−a的图象过第一、三、四象限,反比例函数y=ax的图象分布在第一、三象限,选项A、B、C、D没有符合条件的;
当a<0时,−a>0,则一次函数y=ax−a的图象过第一、二、四象限,反比例函数y=ax的图象分布在第二、四象限,选项A符合条件,B、C、D不符合条件的;
故选:A.
可分a>0和a<0两种情况讨论函数图象经过的象限进行判断即可
本题主要考查函数图象的判断,熟练掌握根据待定系数判断图象在坐标系中的位置是解答本题的关键.
9.【答案】A
【解析】【分析】
此题考查的是用列表法或树状图法求概率的知识.注意画树状图与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.
首先根据题意画出树状图,由树状图求得所有等可能的结果与两次都摸到黄球的情况,然后利用概率公式求解即可求得答案.注意此题属于放回实验.
【解答】
解:画树状图如下:
由树状图可知,共有9种等可能结果,其中两次都摸到黄球的有4种结果,
∴两次都摸到黄球的概率为49,
故选:A.
10.【答案】D
【解析】解:由图可知,抛物线开口向下,对称轴为直线x=−1,与y轴交于(0,1)点,
∴a<0,−b2a=−1,c=1,
∴b=2a<0,
∴abc>0,故B选项结合正确,不合题意;
由图可知,当x=1时y<0,
∴a+b+c<0,故A选项结合正确,不合题意;
由图可知,当x=2时y<0,
∴4a+2b+c<0,故C选项结合正确,不合题意;
∵a<0,c=1,
∴c−a>1,故D选项结论错误,符合题意;
故选:D.
先根据抛物线的开口方向、对称轴、与y轴的交点位置,确定a,b,c的符号,再根据x=1时y<0确定相关式子的符号.
本题考查根据二次函数图象判断式子的符号,熟练掌握二次函数的图象和性质是解题的关键.
11.【答案】D
【解析】解:∵四边形ABCD是正方形,
∴AB=AD=BC=CD= 2,∠DCB=∠COD=∠BOC=90°,OD=OC,
∴BD= 2AB=2,
∴OD=BO=OC=1,
∵将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,
∴DE=DC= 2,DF⊥CE,
∴OE= 2−1,∠EDF+∠FED=∠ECO+∠OEC=90°,
∴∠ODM=∠ECO,
在△OEC与△OMD中
∠EOC=∠DOC=90°OC=OD∠OCE=∠ODM,
△OEC≌△OMD(ASA),
∴OM=OE= 2−1,
故选:D.
根据正方形的性质得到AB=AD=BC=CD= 2,∠DCB=∠COD=∠BOC=90°,OD=OC,求得BD= 2AB=2,得到OD=BO=OC=1,根据折叠的性质得到DE=DC= 2,DF⊥CE,求得OE= 2−1,根据全等三角形的性质即可得到结论.
本题考查了翻折变换(折叠问题),全等三角形的判定和性质,正方形的性质,正确的识别图形是解题的关键.
12.【答案】B
【解析】解:在菱形ABCD中,∠A=60°,
∴△ABD为等边三角形,
设AB=a,由图2可知,△ABD的面积为3 3,
∴△ABD的面积= 34a2=3 3,
解得:a=2 3,
故选:B.
根据图1和图2判定三角形ABD为等边三角形,它的面积为3 3解答即可.
本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此题的关键.
13.【答案】(2+a)(2−a)
【解析】解:4−a2=(2+a)(2−a).
故答案为:(2+a)(2−a).
利用平方差公式a2−b2=(a−b)(a+b),把4−a2写成22−a2的形式即可.
本题考查了公式法分解因式,熟记平方差公式的结构特点是解题的关键,是一道基础题,比较简单.
14.【答案】117
【解析】解:∵a−bb=47,
∴7(a−b)=4b,
∴7a=11b,
∴ab=117.
故答案为:117.
根据两内项之积等于两外项之积列式整理即可得解.
本题考查了比例的性质,熟记两内项之积等于两外项之积是解题的关键.
15.【答案】k≤3且k≠2
【解析】解:∵关于x的一元二次方程(k−2)x2−2x+1=0有实数根,
∴Δ=b2−4ac≥0,
即:4−4(k−2)≥0,
解得:k≤3,
∵关于x的一元二次方程(k−2)x2−2x+1=0中k−2≠0,
故答案为:k≤3且k≠2.
根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于k的不等式,解得即可,同时还应注意二次项系数不能为0.
本题考查了一元二次方程根的判别式,解题的关键是了解根的判别式如何决定一元二次方程根的情况.
16.【答案】18
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD=12,∠ABD=∠CBD=45°,∠C=90°,
∵BE=8,DF=9,
∴CE=4,CF=3,
∴EF= CE2+CF2=5,
作点E关于直线BD的对称点M,则点M在AB上,
则BM=BE=8,
连接MF交BD于G,
则此时GE+GF的值最小,即三角形EFG周长最小,
过F作FN⊥AB于N,
则四边形BCFN是矩形,
∴BN=CF=3,FN=BC=12,
∴MN=8−3=5,
∴FM= FN2+MN2=13,
∴三角形EFG周长的最小值为EG+EF+FG=MF+EF=13+5=18,
故答案为:18.
根据正方形的性质得到AB=BC=AD=CD=12,∠ABD=∠CBD=45°,∠C=90°,根据勾股定理得到EF= CE2+CF2=5,作点E关于直线BD的对称点M,则点M在AB上,则BM=BE=8,连接MF交BD于G,则此时GE+GF的值最小,即三角形EFG周长最小,过F作FN⊥AB于N,根据矩形的性质得到BN=CF=3,FN=BC=12,根据勾股定理即可得到结论.
本题考查了轴对称−最短路径问题,正方形的性质,勾股定理,正确地找出辅助线是解题的关键.
17.【答案】解:(1)原式=2 3+3×2 33−23×4 3
=2 3+2 3−83 3
=4 33;
(2)原式=( 22)2− 33× 32
=12−12
=1.
【解析】(1)直接利用二次根式的性质分别化简,进而得出答案;
(2)直接利用特殊角的三角函数值分别代入,进而化简得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
18.【答案】解:(1)∵2x2+1=3x,
∴2x2−3x+1=0
∴(2x−1)(x−1)=0,
∴2x−1=0或x−1=0,
解得x=12或x=1,
∴原方程的解是x=12或x=1.
(2)x+2y=0①3x−4y=20②,
①×2+②,可得:5x=20,
解得x=4,
把x=4代入①,可得:4+2y=0,
解得:y=−2,
∴原方程组的解是x=4y=−2.
【解析】(1)应用因式分解法,求出一元二次方程的解即可;
(2)应用加减消元法,求出方程组的解即可.
此题主要考查了解二元一次方程组的方法,注意代入消元法和加减消元法的应用;以及因式分解法解一元二次方程,关键是要明确因式分解法解一元二次方程的一般步骤.
19.【答案】证明:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴AC//DF.
【解析】本题考查全等三角形的判定与性质、平行线的判定,解答本题的关键是明确题意,找出所求问题的条件,利用数形结合的思想解答.
要证明AC//DF,只要证明∠ACB=∠DFE即可,要证明∠ACB=∠DFE,只要证明△ABC≌△DEF即可,根据题目中的条件可以证明△ABC≌△DEF,本题得以解决.
20.【答案】(1)13,
(2)画树状图为:
共有12种等可能的结果,甲、乙在相邻跑道的结果数为6,
所以甲、乙在相邻跑道的概率=612=12.
【解析】解:(1)在甲抽到2道的前提下,则乙抽到3道的概率为13;
故答案为:13;
(2)见答案
(1)直接根据概率公式求解;
(2)找出甲、乙在相邻跑道的结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:利用列表或树状图展示所有等可能的结果,再找出某事件所占得结果数,然后根据概率公式计算这个事件的概率.
21.【答案】解:设售价定为x元,
[600−10(x−40)](x−30)=10000,
整理,得x2−130x+4000=0,
解得:x1=50,x2=80(舍去).
600−10(x−40)=600−10×(50−40)=500(个).
答:台灯的定价定为50元,这时应进台灯500个.
【解析】设售价定为x,那么就少卖出10(x−40)个,根据利润=售价−进价,可列方程求解.
本题考查一元二次方程的应用,关键是看到定价和销售量的关系,根据利润列方程求解.
22.【答案】x<−3或0
∴反比例解析式为y=6x,
把B(−3,n)代入反比例解析式得:n=−2,即B(−3,−2),
把A与B代入一次函数解析式得:2k+b=3−3k+b=−2,
解得:k=1,b=1,即一次函数解析式为y=x+1;
(2)∵A(2,3),B(−3,−2),
∴由图象得:kx+b
(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值即可;
(2)利用图象找出所求不等式的解集即可;
(3)以BC为底,A与B横坐标相减为高求出三角形面积即可.
此题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数与一次函数性质是解本题的关键.
23.【答案】2
【解析】解:(1)∵AC=6,BC=8,点P沿边AC向C以每秒3个单位长度的速度运动,点Q沿边BC向B以每秒4个单位长度的速度运动,
∴当运动停止时,t的值为6÷3=8÷4=2,
故答案为:2;
(2)①由已知可得:CP=−3t+6,CQ=4t,
∴S=12×(−3t+6)⋅4t=−6t2+12t(0
且−6<0,
∴t=1时,S的值最大为6.
(1)①由已知可得,当运动停止时,t的值为6÷3=8÷4=2;
(2)①由已知可得:CP=−3t+6,CQ=4t,即可得S=−6t2+12t;
②由S=−6t2+12t=−6(t−1)2+6,即可得t=1时,S的值最大为6.
本题考查函数的综合应用,涉及动点问题、三角形面积等知识,解题的关键是用含t的代数式表示AP、CQ的长度.
24.【答案】解:∵GC//AB,
∴GCAB=DCDB,即1.5AB=33+BC,
∵HE//AB,
∴HEAB=EFFB,即1.5AB=510+BC,
∴33+BC=510+BC,
∴BC=7.5米,
∴AB=5.25米,
∴灯杆AB的高度为5.25米.
【解析】根据GC//AB可得GCAB=DCDB,即1.5AB=33+BC,再由HE//AB可得HEAB=EFFB,即1.5AB=510+BC,进而可得33+BC=510+BC,再解即可得到BC,进而可得AB的长.
此题主要考查了相似三角形的应用,解答本题的关键是掌握相似三角形的对应边的比相等.
25.【答案】(1)证明:∵∠DAB=30°,∠DBC=∠A+∠ADB=60°,
∴∠A=∠ADB=30°,
∴BD=AB;
(2)解:∵AB=50m,
∴BD=50m,
又∵∠DCB=90°,
∴CD=BD⋅sin∠CBD=50× 32=25 3(m),
∴塔CD的高为25 3m.
【解析】(1)根据三角形的外角的性质可得∠A=∠ADB=30°,进而根据等角对等边即可得出AB=BD;
(2)解Rt△BCD,即可求解.
本题考查了解直角三角形的应用−仰角俯角问题,解答本题的关键是借助仰角找到直角三角形各边之间的联系.
26.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∵AF=AB,
∴BE=AF,
又∵BE//AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴平行四边形ABEF是菱形;
(2)解:∵四边形ABEF为菱形,
∴AF=AB=10,AG⊥BF,
又∵BF=10,
∴BG=FG=5,
∴AG= 102−52=5 3,
∴AE=2AG=10 3,
∴菱形ABEF的面积12×10×10 3=50 3.
【解析】(1)由平行四边形的性质和角平分线得出∠BAE=∠AEB,证出BE=AB,由AF=AB得出BE=AF,即可得出结论.
(2)根据菱形的性质得到AB=BF=10,BG=FG=5,利用勾股定理求出AG,进而求出结论.
本题主要考查了菱形的性质和判定,勾股定理,关键是掌握一组邻边相等的平行四边形是菱形,菱形对角线互相垂直且平分.
27.【答案】解:(1)将A(2,5),C(0,−3)代入二次函数解析式得:4+2b+c=5c=−3,
解得:b=2c=−3,
则二次函数解析式为y=x2+2x−3;
(2)作出函数图象,如图所示:
根据图象得:当−3≤x≤1时,y的取值范围为−4≤y≤0.
【解析】(1)将A与C坐标代入二次函数解析式求出b与c的值,即可确定出解析式;
(2)做出二次函数图象,根据图象及x的范围即可确定出y的范围.
此题考查了待定系数法求二次函数解析式,二次函数的性质,以及二次函数与x轴的交点,熟练掌握待定系数法是解本题的关键.
28.【答案】(1)证明:如图1中,
∵四边形ABCD是正方形,
∴DA=DC,∠A=∠ADC=∠DCB=∠DCF=90°,
∵DE⊥DF,
∴∠EDF=∠ADC=90°,
∴∠ADE=∠CDF,
在△DAE和△DCF中,
∠ADE=∠CDFDA=DC∠A=∠DCF,
∴△DAE≌△DCF(ASA),
∴AE=CF.
(2)解:EA+EC= 2DE.
理由:如图2中,过点D作DH⊥EC于点H,DP⊥EA交EA的延长线于点P.
∵DP⊥EA, DH⊥EC,AE⊥EC,
∴∠DPA=90°,∠DHC=90°,∠AEC=90∘
∴四边形DPEH为矩形,
∴∠PDH=90°,
∵四边形ABCD是正方形
∴∠ADC=90°, AD=DC,
∴∠PDA=∠HDC,
在△DPA和△DHC中,{∠PDA=∠HDC∠DPA=∠DHC=90∘DA=DC,
∴△DPA≌△DHC(AAS)r
∴DP=DH, AP=CH,
∴四边形DPEH为正方形,
∴EP=EH,
∴EA+EC=EP−AP+EH+CH=2EP,
∵DE= 2EP,
∴EA+EC= 2DE.
(3)解:
过点D作DP⊥EA,交EA的延长线于P,作DH⊥EC于H,
∵DP⊥EA,DH⊥EC,AE⊥EC
∴∠DPA=90°,∠DHC=90°,∠AEC=90∘
∴四边形DPEH为矩形,
∴∠PDH=90°,
∵四边形ABCD是正方形
∴∠ADC=90°, AD=DC,
∴∠PDA=∠HDC,
在△DPA和△DHC中,{∠PDA=∠HDC∠DPA=∠DHC=90∘DA=DC,
∴△DPA≌△DHC(AAS)r
∴DP=DH, AP=CH,
∴四边形DPEH为正方形,
∴∠AEF=∠FEH=45∘,
∴∠AED=∠DEC=45°,
由(2)可知,AE+EC= 2DE,
∵AE⊥AF,
∴∠EAF=90°,
∴∠AEF=∠AFE=45°,
∴AE=AF= 2,
∴EF= 2AE=2,
∵DF=3,
∴DE=5,
∴ 2+EC=5 2,
∴EC=4 2.
【解析】(1)证明△DAE≌△DCF(ASA),可得结论.
(2)结论:EA+EC= 2DE.如图2中,过点D作DH⊥EC于点H,DP⊥EA交EA的延长线于点P.利用全等三角形的性质证明EP=EH,AP=CH,可得结论.
(3)如图3中,过点D作DP⊥EA,交EA的延长线于P,作DH⊥EC于H,证明∠AED=∠DEC=45°,利用(2)中结论求解即可.
本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,正方形的判定,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用建模的思想思考问题,属于中考压轴题.
2023-2024学年甘肃省兰州一中七年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年甘肃省兰州一中七年级(上)期末数学试卷(含详细答案解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年甘肃省兰州市红古区七年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年甘肃省兰州市红古区七年级(上)期末数学试卷(含详细答案解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年甘肃省兰州二十二中七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年甘肃省兰州二十二中七年级(上)期末数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












