新教材2023版高中数学第1章导数及其应用章末复习课课件湘教版选择性必修第二册

这是一份新教材2023版高中数学第1章导数及其应用章末复习课课件湘教版选择性必修第二册，共24页。

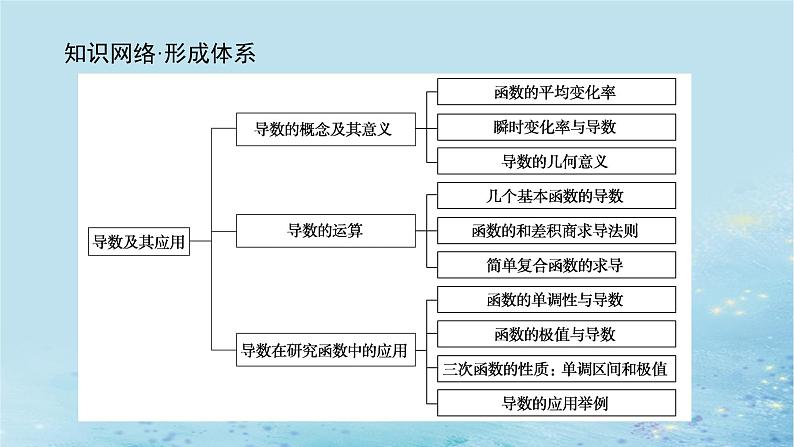
章末复习课知识网络·形成体系考点聚焦·分类突破考点一　导数几何意义的应用1．导数几何意义的应用，主要考查切线方程及切点．(1)明确“过点P(x0，y0)的曲线y＝f(x)的切线方程”与“在点P(x0，y0)处的曲线y＝f(x)的切线方程”的异同点．(2)围绕着切点有三个等量关系：切点(x0，y0)，则k＝f′(x0)，y0＝f(x0)，(x0，y0)满足切线方程，在求解参数问题中经常用到．2．通过对导数几何意义的考查，提升学生的数学运算、数学抽象核心素养． 答案：C　  答案：B　 (3)已知直线y＝kx＋b与曲线y＝x3＋ax＋1相切于点(2，3)，则b＝________．答案：－15　解析：(3)设f(x)＝x3＋ax＋1，由题意知f(2)＝3，则a＝－3.f(x)＝x3－3x＋1，f′(x)＝3x2－3，f′(2)＝3×22－3＝9＝k，又点(2，3)在直线y＝9x＋b上，∴b＝3－9×2＝－15.(4)曲线C：y＝x3－3x和直线x＝a(a>0)的交点为P，过P点的曲线C的切线与x轴交于点Q(－a，0)，求a的值． 考点二　利用导数研究函数的单调性1．利用导数研究函数的单调性是高考中最常见的考查方式，其特点是导数f′(x)的符号一般由二次函数来确定；经常同一元二次方程、一元二次不等式结合，融分类讨论、数形结合于一体．2．通过对用导数研究函数的单调性的考查，提升学生的逻辑推理、直观想象及数学运算核心素养． 答案：D　   综上：当a≤1时，f(x)的单调递增区间为(1，＋∞)，单调递减区间为(0，1)；当1e时，f(x)的单调递增区间为(0，1)，(ln a，＋∞)；单调递减区间为(1，ln a)．考点三　利用导数研究函数的极值与最值1．利用导数研究函数的极值与最值，主要是以ln x，ex，－x3等线性函数(或复合函数)为载体，研究函数的极值与最值问题．2．通过对函数的极值与最值问题的考查，提升学生的逻辑推理、直观想象及数学运算核心素养． 答案：B　    考点四　利用导数证明不等式1．对于某些不等式的证明，常常通过构造函数，利用导数的性质讨论函数的单调性进行证明．这种构造转换的过程与方法，体现了深刻的化归思想．2．通过对利用导数证明不等式的考查，提升学生的逻辑推理、数学运算核心素养．    考点五　利用导数解决优化问题1．利用导数解决实际问题中的最大、最小值问题，是函数内容的继续与延伸，这种解决问题的方法使复杂的问题简单化，因而也成为高考的又一新热点．2．通过对利用导数解决实际问题的考查，提升学生的数学建模、逻辑推理及数学运算核心素养．例5　某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度)．设该蓄水池的底面半径为r米，高为h米，体积为V立方米．假设建造成本仅与表面积有关，侧面的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12 000π元(π为圆周率)．(1)将V表示成r的函数V(r)，并求该函数的定义域； (2)讨论函数V(r)的单调性，并确定r和h为何值时该蓄水池的体积最大．