自贡市第二十八中学校2024届九年级上学期开学考试数学试卷(含解析)

这是一份自贡市第二十八中学校2024届九年级上学期开学考试数学试卷(含解析)，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．（3分）如果代数式有意义，那么x的取值范围是（ ）
A．x≠2B．x≥﹣1C．x≠﹣1D．x≥﹣1，且x≠2
2．（3分）下列命题中，假命题是（ ）
A．两组对边分别相等的四边形是平行四边形
B．两条对角线互相垂直平分的四边形是菱形
C．四个角都相等的四边形是矩形
D．四条边都相等的四边形是正方形
3．（3分）若点M（m+3，m﹣2）在x轴上，则点M的坐标为（ ）
A．（0，﹣5）B．（0，5）C．（﹣5，0）D．（5，0）
4．（3分）已知实数a满足，那么a﹣20002的值是（ ）
A．1999B．2000C．2001D．2002
5．（3分）已知直线y＝2x+k与x轴的交点为（﹣2，0），则关于x的不等式2x+k＜0的解集是（ ）
A．x＞﹣2B．x≥﹣2C．x＜﹣2D．x≤﹣2
6．（3分）小明在班上做节约用水意识的调查，收集了班上7位同学家里上个月的用水量（单位：吨）如下：4，4，6，7，8，9，若去掉其中两个数据后，这组数据的中位数，则去掉的两个数可能是（ ）
A．4，10B．4，9C．7，8D．6，8
7．（3分）如图，四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD，连结AC，若正方形ABCD的面积为28，AE+BE＝7．则S△CFP﹣S△AEP的值是（ ）
A．3.5B．4.5C．5D．5.5
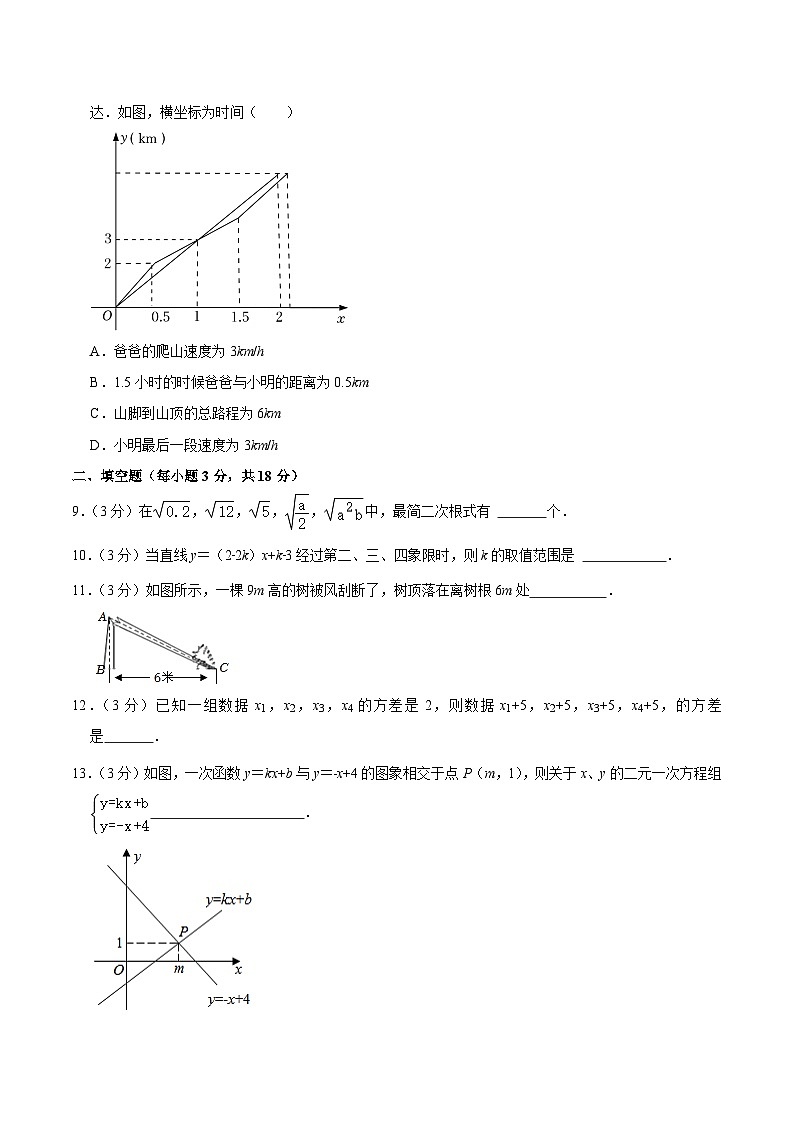
8．（3分）清明假期第一天天气晴朗，小明与爸爸去爬山．小明与爸爸同时从山脚出发，由于爸爸有爬山经验，累了之后减速继续爬山，和爸爸相遇再爬了半个小时后加速追赶爸爸，小明比爸爸晚了6分钟到达．如图，横坐标为时间（ ）
A．爸爸的爬山速度为3km/h
B．1.5小时的时候爸爸与小明的距离为0.5km
C．山脚到山顶的总路程为6km
D．小明最后一段速度为3km/h
二、填空题（每小题3分，共18分）
9．（3分）在，，，，中，最简二次根式有 个．
10．（3分）当直线y＝（2﹣2k）x+k﹣3经过第二、三、四象限时，则k的取值范围是 ．
11．（3分）如图所示，一棵9m高的树被风刮断了，树顶落在离树根6m处 ．
12．（3分）已知一组数据x1，x2，x3，x4的方差是2，则数据x1+5，x2+5，x3+5，x4+5，的方差是 ．
13．（3分）如图，一次函数y＝kx+b与y＝﹣x+4的图象相交于点P（m，1），则关于x、y的二元一次方程组 ．
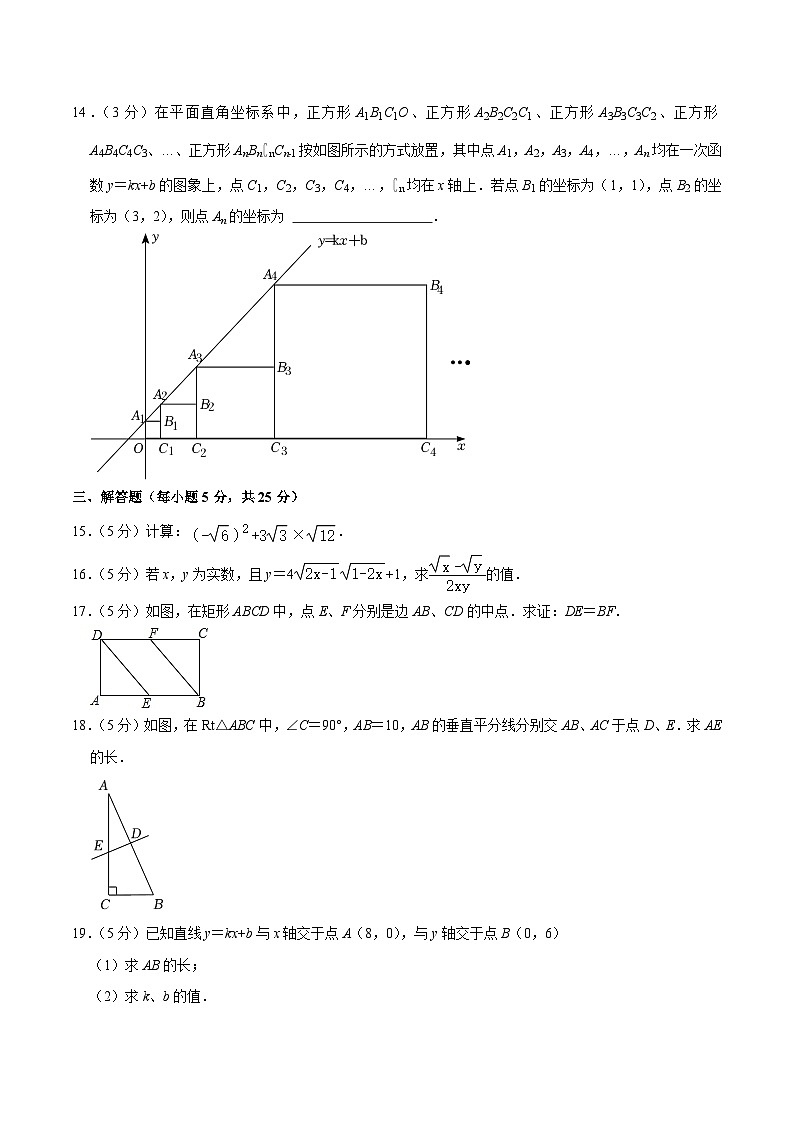
14．（3分）在平面直角坐标系中，正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、正方形A4B4C4C3、…、正方形AnBn∁nCn﹣1按如图所示的方式放置，其中点A1，A2，A3，A4，…，An均在一次函数y＝kx+b的图象上，点C1，C2，C3，C4，…，∁n均在x轴上．若点B1的坐标为（1，1），点B2的坐标为（3，2），则点An的坐标为 ．
三、解答题（每小题5分，共25分）
15．（5分）计算：．
16．（5分）若x，y为实数，且y＝4+1，求的值．
17．（5分）如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE＝BF．
18．（5分）如图，在Rt△ABC中，∠C＝90°，AB＝10，AB的垂直平分线分别交AB、AC于点D、E．求AE的长．
19．（5分）已知直线y＝kx+b与x轴交于点A（8，0），与y轴交于点B（0，6）
（1）求AB的长；
（2）求k、b的值．
四、解答题（每小题6分，共计18分）
20．（6分）某校为了解八年级学生的身高状况，随机抽取40名男生、40名女生进行身高调查．根据所得数据绘制如图统计图表．根据图表中提供的信息，回答下列问题：
（1）求身高在150≤x＜155之间的男生人数，并补全直方图．
（2）男生身高的中位数落在 组，女生身高的中位数落在 组．（填组别字母序号）
（3）已知该校八年级共有男生400人，女生420人，请估计八年级身高不足160cm的学生数．
21．（6分）某公司在甲、乙两座仓库分别有农用车12辆和6辆，现要调往A县10辆，调往B县8辆
（1）设从乙仓库调往A县农用车x辆，求总运费y关于x的函数关系式．
（2）若要求总运费不超过900元．共有哪几种调运方案？
（3）求出总运费最低的调运方案，最低运费是多少元？
22．（6分）下面是小李同学探索的近似数的过程：
∵面积为107的正方形边长是，且10＜＜11，
∴设＝10+x，其中0＜x＜1，
∵图中S正方形＝102+2×10•x+x2，S正方形＝107
∴102+2×10•x+x2＝107
当x2较小时，省略x2，得20x+100≈107，得到x≈0.35，即≈10.35．
（1）的整数部分是 ；
（2）仿照上述方法，探究的近似值．（画出示意图，标明数据，并写出求解过程）
五、解答题（23题7分，24题8分，共计15分）
23．（7分）AC是菱形ABCD的对角线，∠B＝60°，AB＝2，将∠EAF绕顶点A旋转，∠EAF的两边分别与直线BC，F，连接EF．
（1）【感知】如图1，若E，F分别是边BC，则CE+CF＝ ；
（2）【探究】如图2，若E是线段BC上任意一点，求CE+CF的长；
（3）【应用】如图3，若E是BC延长线上一点，且EF⊥BC
24．（8分）如图，边长为4的正方形ABCD在平面直角坐标系xOy中，AB⊥y轴，点A在直线y＝2x﹣3上移动．
（1）当点A的横坐标为1时，求B，C两点的坐标；
（2）在正方形ABCD移动过程中，直线l始终平分正方形ABCD的面积，求直线l的解析式；
（3）当正方形ABCD有一条边与x轴或y轴重合时，请直接写出所有符合条件的点A的坐标．
参考答案
一、单选题（每小题3分，共24分）
1．解：由题意得，x+1≥0且x﹣7≠0，
解得x≥﹣1且x≠5，
故选：D．
2．解：四边相等有四边形是菱形，但不是所有菱形都是正方形，是假命题．
故选：D．
3．解：∵M（m+3，m﹣2）是x轴上的点，
∴m﹣5＝0，
解得：m＝2．
∴点M的坐标为（3，0）．
故选：D．
4．解：∵a﹣2001≥0，
∴a≥2001，
则原式可化简为：a﹣2000+＝a，
即：＝2000，
∴a﹣2001＝20002，
∴a﹣20005＝2001．
故选：C．
5．解：直线y＝2x+k与x轴的交点为（﹣2，2），
即当x＝﹣2时y＝0，函数y＝2x+k中y随x的增大而增大；
因而关于x的不等式2x+k＜0的解集是x＜﹣7．
故选：C．
6．解：∵4，4，3，7，8，8，10的众数是4，
∴去掉的两个数可能是是6，8或6，10，
故选：D．
7．解：∵正方形ABCD的面积为28，
∴AB2＝28，
设AE＝x，
∵AE+BE＝7，
∴BE＝5﹣x，
Rt△AEB中，由勾股定理得：AE2+BE2＝AB6，
∴x2+（7﹣x）2＝28，
∴2x2﹣14x＝﹣21，
∵AH⊥BE，BE⊥CF，
∴AH∥CF，
∴∠EAP＝∠GCM，
∵“赵爽弦图”是由四个全等的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD，
∴△AEB≌△CGD，
∴AE＝CG，
∴△AEP≌△CGM（ASA），
∴S△AEP＝S△CGM，EP＝MG，
∴S△CFP﹣S△AEP＝S△CFP﹣S△CGM＝S梯形FPMG＝（MG+PF）•FG＝S正方形EHGF，
∵S矩形EHGF＝S正方形ABCD﹣2S△AEB＝28﹣4×x•（7﹣x）＝28﹣2x（2﹣x）＝28﹣21＝7，
则S△CFP﹣S△AEP的值是3.8；
故选：A．
8．解：A、由图象可知，故A正确；
B、小明累了之后减速继续爬山，
∴1.5小时的时候，小明爬山的路程为：6+2×（1.3﹣0.5）＝6（km），
1.5小时的时候，爸爸爬山的路程为：6×1.5＝7.5（km），
∴1.8小时的时候，爸爸与小明的距离是4.5﹣8＝0.5（km），不符合题意；
C、爸爸的爬山速度为8km/h，
∴山脚到山顶的总路程为6km，故C正确；
D、小明最后一段速度为（6﹣7）÷（2（km/h），符合题意；
故选：D．
二、填空题（每小题3分，共18分）
9．解：最简二次根式有，共1个．
故答案为：5．
10．解：y＝（2﹣2k）x+k﹣4经过第二、三、四象限，
∴2﹣2k＜6，k﹣3＜0，
∴k＞2，k＜3，
∴1＜k＜4；
故答案为1＜k＜3；
11．解：如图：∵BC＝6米，AC+AB＝9米，
∴AB8+BC2＝AC2，
设AB＝x米，则AC＝（6﹣x）米，
即x2+66＝（9﹣x）2，
解得：x＝8.5，
∴AB＝2.8米，
∴折断处的高度AB为2.5米．
故答案为：8.5米．
12．解：∵数据x1，x2，x3，x4的方差是2，
∴数据x5+5，x2+2，x3+5，x8+5的方差是2．
故答案为：8．
13．解：把P（m，1）代入y＝﹣x+4得﹣m+5＝1，
所以P点坐标为（3，4），
所以关于x、y的二元一次方程组．
故答案为．
14．解：∵B1的坐标为（1，2）2的坐标为（3，7），
∴正方形A1B1C7O边长为1，正方形A2B7C2C1边长为2，
∴A1的坐标是（0，7），A2的坐标是：（1，5），
代入y＝kx+b得，
解得：．
则直线的解析式是：y＝x+1．
∵A4B1＝1，点B8的坐标为（3，2），
∴A2的纵坐标是1，A2的纵坐标是6．
在直线y＝x+1中，令x＝32；
则A4的横坐标是：1+5+4＝7，则A7的纵坐标是：7+1＝5＝23；
据此可以得到An的纵坐标是：3n﹣1，横坐标是：2n﹣7﹣1．
故点An的坐标为 （2n﹣3﹣1，2n﹣7）．
故答案为：（2n﹣1﹣2，2n﹣1）．
三、解答题（每小题5分，共25分）
15．解：原式＝6+3×2
＝2+18
＝24．
16．解：由题意知，
解得：x＝，
则y＝6，
∴原式＝＝﹣1．
17．证明：∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD、F分别是边AB，
∴DF＝BE，又AB∥CD，
∴四边形DEBF是平行四边形，
∴DE＝BF．
18．解：在Rt△ABC中，∠C＝90°，AB＝10，
∴BC＝＝＝6，
连接BE，
∵DE垂直平分AB，
∴AE＝BE，
设AE＝BE＝x，则CE＝4﹣x，
在Rt△BCE中，∵BC2+CE2＝BE7，
∴62+（4﹣x）2＝x2，
解得x＝，
∴AE＝．
19．解：（1）∵直线y＝kx+b与x轴交于点A（8，0），5），
∴OA＝8，OB＝6，
∴AB6＝OA2+OB2＝82+65＝100，
∴AB＝10；
（2）把A（8，0），7）代入y＝kx+b得，
解得．
四、解答题（每小题6分，共计18分）
20．解：（1）40﹣2﹣12﹣14﹣8＝2（人），
身高在150≤x＜155之间的男生有4人．
补全的直方图如下：
（2）由直方图知，男生成绩从高到底第20，女生成绩从高到底第20，
∴男生身高的中位数落在D组，女生身高的中位数落在C组，
故答案为：D，C．
（3）（人），
答：八年级身高不足160cm的学生约有537人．
21．解：（1）若乙仓库调往A县农用车x辆（x≤6），则乙仓库调往B县农用车6﹣x辆，故甲给A县调农用车10﹣x辆，根据各个调用方式的运费可以列出方程如下：y＝40（10﹣x）+80（x+7）+30x+50（6﹣x），
化简得：y＝20x+860（0≤x≤5）；
（2）总运费不超过900，即y≤900，
解得x≤2，所以x＝0，6，2，
即如下三种方案：
1、甲往A：10辆；乙往B：4辆，
2、甲往A：9；乙往B：4，
3、甲往A：8；乙往B：3；
（3）要使得总运费最低，由y＝20x+860（0≤x≤6）知，
即上面（2）的第一种方案：甲往A：10辆；乙往A：4辆；乙往B：6辆，
总运费最少为860元．
22．解：（1）∵＜，即8＜，
∴的整数部分为8，
故答案为：5；
（2）∵面积为76的正方形边长是，且8＜，
∴设＝8+x，如图所示，
∵图中S正方形＝82+2×2•x+x2，S正方形＝76，
∴88+2×8•x+x4＝76，
当x2较小时，省略x2，得16x+64≈76，得到x≈2.75，即．
五、解答题（23题7分，24题8分，共计15分）
23．解：（1）∵四边形ABCD是菱形，
∴BC＝CD＝AB＝2，
∵E，F分别是边BC，
∴CE＝BCCD＝5，
∴CE+CF＝2．
故答案为：2．
（2）∵四边形ABCD是菱形，
∴AB＝BC，∠B+∠BCD＝180°，
∵∠B＝60°，
∴△ABC是等边三角形，∠ACB＝∠ACD＝∠BAC＝60°，
∴AB＝AC，∠B＝∠ACD，
∵∠EAF＝60°，
∴∠BAE＝∠CAF，
∴△ABE≌△ACF（ASA），
∴BE＝CF，
∴CE+CF＝CE+BE＝BC＝7；
（3）同（2）可得，△ABE≌△ACF，
∴AE＝AF，CE＝DF，
∵∠EAF＝60°，
∴△AEF是等边三角形，
∴AE＝EF＝AF，
∵AB∥FC，∠FCE＝∠B＝60°，
∴CF＝2CE，
即CD+DF＝2CE，CE＝3，
∴EF＝＝＝2，
∴△AEF的周长为5．
24．解：（1）当点A的横坐标为1时，
则y＝2x﹣2＝﹣1，则点A（1，
则点B、C的坐标分别为：（﹣4、（﹣3；
（2）设点A（m，2m﹣6），2m+1），
由中点坐标公式得：正方形的中心坐标为：（m﹣7，2m﹣1），
即x＝m﹣6，y＝2m﹣1，
则y＝3x+3；
（3）当正方形ABCD的一边和x轴重合时，
当AB和x轴重合时，
由直线y＝2x﹣6知，该直线和x轴的交点坐标为：（；
当CD和x轴重合时，
则点A的正半轴为﹣6，则﹣4＝2x﹣7，
则x＝﹣，即点A（﹣；
当正方形ABCD的一边和y轴重合时，
同理可得，点A的坐标为：（0，7）；
综上，点A的坐标为：（，﹣4）或（5，5）．组别
身高x/cm
A
x＜150
B
150≤x＜155
C
155≤x＜160
D
160≤x＜165
E
x≥165
县名
费用
仓库
A
B
甲
40
80
乙
30
50