【精品同步练习】沪科版八年级数学上册第十二周测试题（11章-15章）（知识梳理+含答案）

这是一份【精品同步练习】沪科版八年级数学上册第十二周测试题（11章-15章）（知识梳理+含答案），文件包含沪科版八年级数学上册第十二周测试题11章-15章原卷版docx、沪科版八年级数学上册第十二周测试题11章-15章解析版docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。

一、单选题
1．下列各点中，在第三象限的点是（ ）
A．（5，3）B．（5，﹣3）C．（﹣5，﹣3）D．（﹣5，3）
【答案】C
【分析】根据第三象限内点的坐标特征：（-，-）解答即可．
【详解】解：因为第三象限的点的横坐标小于0，纵坐标小于0，
所以在第三象限的点是（﹣5，﹣3）．
故选C．
【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
2．下列手机app的lg中，是轴对称图形的是（ ）
A．B．C．D．
【答案】D
【分析】根据轴对称图形的概念“把一个图形沿某条直线折叠，直线两旁的部分能完全重合的图形是轴对称图形”对各选项分析判断即可得解．
【详解】解：A、不是轴对称图形，故本选项不符合题意；
B、不是轴对称图形，故本选项不符合题意；
C、不是轴对称图形，故本选项不符合题意；
D、是轴对称图形，故本选项符合题意．
故选：D．
【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
3．函数中，自变量的取值范围是（ ）
A．B．C．D．
【答案】B
【分析】利用分式的分母不能等于零即可求解．
【详解】解：由题意得，，
解得，
故选：B
【点睛】本题考查了函数自变量的取值范围，利用分式的分母不等于零是解题的关键．
4．一个等腰三角形的周长为13cm，一边长为5cm，则另两边长分别为（ ）
A．3cm，13cmB．4cm，4cm
C．3cm，5cm或4cm，4cmD．以上都不对
【答案】C
【分析】分5cm长的边是等腰三角形的腰和是等腰三角形的底边两种情况进行讨论，即可求解．
【详解】解：当长的边是等腰三角形的腰时，则其底边是，三条边为，，，能够组成三角形；
当5cm长的边是等腰三角形的底边时，则其腰长是，三条边为，，，能够组成三角形．
故另两边长分别为，或，．
故选C．
【点睛】本题考查等腰三角形的定义及三角形的三边关系，掌握分类讨论思想是解题的关键．
5．如图，在中，．分别以点为圆心，大于的长为半径画弧，两弧相交于点，作直线分别交，于点．以为圆心，长为半径画弧，交于点，连结．则下列说法错误的是（ ）
A．B．
C．D．
【答案】C
【分析】根据线段垂直平分线的判定与性质即可判断选项A；先根据等腰三角形的性质可得，从而可得，再根据等腰三角形的性质可得，然后根据三角形的外角性质可得，由此即可判断选项B；先假设可得，再根据角的和差可得，从而可得，由此即可判断选项C；先根据等腰三角形的判定可得，再根据相似三角形的判定可得，然后根据相似三角形的性质可得，最后根据等量代换即可判断选项D．
【详解】解：由题意可知，垂直平分，，
，则选项A正确；
，
，
，，
，，
，，
，
，则选项B正确；
假设，
，
又，
，
，与矛盾，
则假设不成立，选项C错误；
，，
，
在和中，，
，
，即，
，则选项D正确；
故选：C．
【点睛】本题考查了线段垂直平分线的性质、等腰三角形的判定与性质、全等三角形的性质、相似三角形的判定与性质，综合性较强，熟练掌握判定定理与性质是解题关键．
6．如图，在△ABC中，∠A＝36°，AB＝AC，AB的垂直平分线交AB于点O，交AC于点D，连接BD，下列结论错误的是（ ）
A．BD平分∠ABCB．∠C＝2∠AC．AB=CD+BCD．S△BCD＝S△BOD
【答案】D
【分析】根据等腰三角形的性质结合三角形内角和定理可求出∠C＝∠ABC＝72°，即得出∠C＝2∠A，可判断B；由线段垂直平分线的性质可知AD＝BD，从而可求出∠A＝∠ABD＝36°，进而得出∠DBC＝36°＝∠ABD，可判断A；易判断△BDC，△ABC、△ADB是等腰三角形，从而可得CD+BC＝AB，可判断C；由已知不能推出△BCD的面积和△BOD面积相等，故D无法确定．
【详解】∵∠A＝36°，AB＝AC，
∴∠C＝∠ABC＝72°，
∴∠C＝2∠A，故B正确，不符合题意；
∵DO是AB垂直平分线，
∴AD＝BD，
∴∠A＝∠ABD＝36°，
∴∠DBC＝72°-36°＝36°＝∠ABD，
∴BD是∠ABC的角平分线，故A正确，不符合题意；
∵∠BDC＝∠ABD+∠A=72°，
∴∠BDC＝∠C，
∴△BDC是等腰三角形．
由A、B可知△ABC、△ADB是等腰三角形，
∴CD+BC＝CD+BD＝CD+AD＝AC＝AB，故C正确，不符合题意；
根据已知不能推出△BCD的面积和△BOD面积相等，故D错误，符合题意．
故选D．
【点睛】本题考查线段垂直平分线的性质，三角形内角和定理，等腰三角形的判定和性质，角平分线的判定．熟练掌握上述知识是解题关键．
7．一次函数的图象经过原点，则（ ）
A．B．C．D．
【答案】B
【分析】把原点坐标代入函数解析式可得b的值，然后根据一次函数的定义可得k的取值范围，问题得解．
【详解】解：由一次函数的意义可得k≠0,
∵一次函数 y=kx+b 的图象经过原点，
∴0=k×0+b，
∴b=0，
故选B ．
【点睛】本题考查一次函数的应用，熟练掌握一次函数的定义及由函数图象上点的坐标求解析式参数的方法是解题关键．
8．如图，等腰△中，点D，E分别在腰AB，AC上，添加下列条件，不能判定≌的是（ ）
A．B．C．D．
【答案】B
【分析】根据全等三角形的判定方法逐项判断即得答案．
【详解】解： A、若添加，由于AB=AC，∠A是公共角，则可根据SAS判定≌，故本选项不符合题意；
B、若添加，不能判定≌，故本选项符合题意；
C、若添加，由于AB=AC，∠A是公共角，则可根据AAS判定≌，故本选项不符合题意；
D、若添加，∵AB=AC，∴∠ABC=∠ACB，∴∠ABE=∠ACD，由于∠A是公共角，则可根据ASA判定≌，故本选项不符合题意．
故选：B．
【点睛】本题考查了全等三角形的判定和等腰三角形的性质，属于基本题型，熟练掌握全等三角形的判定方法是解题的关键．
9．一次函数（k为常数，k≠0）和．当x＜2时，＞，则k取值范围（ ）
A．k≤﹣2B．﹣2≤k≤1且k≠0
C．k≥1D．﹣2＜k＜1且k≠0
【答案】B
【分析】解不等式kx+3＞x﹣3，根据题意得出k﹣1＜0且2且k≠0，解此不等式组即可．
【详解】解：∵一次函数（k为常数，k≠0）和．当x＜2时，＞，
∴kx+3＞x﹣3，
∴kx﹣x＞﹣6，
∴（k－1）x＞﹣6，
∴k﹣1＜0且2且k≠0，
当k﹣1＜0即k＜1时，2则k≥﹣2，
所以不等式组的解集为﹣2≤k＜1且k≠0；
当k＝1时，，，很明显＞也成立，
故k的取值范围是﹣2≤k≤1且k≠0，
故选：B．
【点睛】本题考查了一次函数与一元一次不等式组，一次函数的性质，关键是根据题意得出k﹣1＜0时，2且k≠0解答．
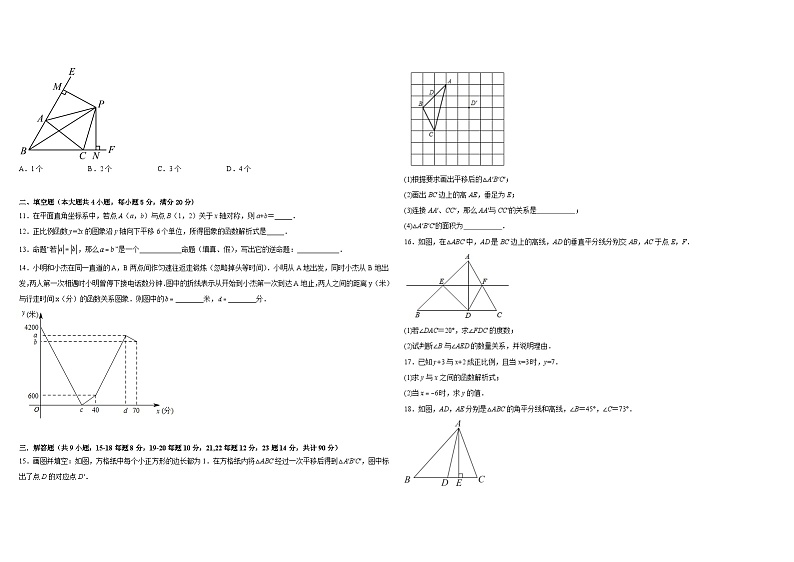
10．如图，△ABC中，∠ABC、∠FCA的角平分线BP、CP交于点P，延长BA、BC，PM⊥BE于M，PN⊥BF于N，则下列结论：①AP平分∠EAC；②；③；④．其中正确结论的个数是（ ）
A．1个B．2个C．3个D．4个
【答案】D
【分析】过点P作PD⊥AC于D，根据角平分线的判定定理和性质定理判断①；证明Rt△PAM≌Rt△PAD，根据全等三角形的性质得出∠APM＝∠APD，同理得出∠CPD＝∠CPN，可判断②；根据三角形的外角性质判断③；根据全等三角形的性质判断④．
【详解】解：①过点P作PD⊥AC于D，
∵PB平分∠ABC，PC平分∠FCA，PM⊥BE，PN⊥BF，PD⊥AC，
∴PM＝PN，PN＝PD，
∴PM＝PN＝PD，
∴AP平分∠EAC，故①正确；
②∵PM⊥AB，PN⊥BC，
∴∠ABC+90°+∠MPN+90°＝360°，
∴∠ABC+∠MPN＝180°，
在Rt△PAM和Rt△PAD中，
，
∴Rt△PAM≌Rt△PAD（HL），
∴∠APM＝∠APD，
同理：Rt△PCD≌Rt△PCN（HL），
∴∠CPD＝∠CPN，
∴∠MPN＝2∠APC，
∴∠ABC+2∠APC＝180°，②正确；
③∵PC平分∠FCA，BP平分∠ABC，
∴∠ACF＝∠ABC+∠BAC＝2∠PCN，∠PCN＝∠ABC+∠BPC，
∴
∴∠BAC＝2∠BPC，③正确；
④由②可知Rt△PAM≌Rt△PAD（HL），Rt△PCD≌Rt△PCN（HL）
∴S△APD＝S△APM，S△CPD＝S△CPN，
∴S△APM+S△CPN＝S△APC，故④正确，
故选：D
【点睛】本题考查的是角平分线的性质、全等三角形的判定和性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
二、填空题
11．在平面直角坐标系中，若点A（a，b）与点B（1，2）关于x轴对称，则a+b＝_____．
【答案】-1
【分析】直接利用关于轴对称点的性质（横坐标不变，纵坐标互为相反数）得出，的值，进而得出答案．
【详解】解：点与点关于轴对称，
，，
的值是：．
故答案为：．
【点睛】此题主要考查了关于轴对称点的性质，正确把握横纵坐标的关系是解题关键．
12．正比例函数y=2x的图象沿y轴向下平移6个单位，所得图象的函数解析式是_____．
【答案】y=2x-6##y=-6+2x
【分析】直接根据“上加下减”的原则进行解答即可．
【详解】解：由“上加下减”的原则可知：将正比例函数的图象向下平移6个单位，则平移后所得图象的解析式是．
故答案为：．
【点睛】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
13．命题“若，那么”是一个____________命题（填真、假），写出它的逆命题：____________．
【答案】 假 若，那么．
【分析】根据绝对值的意义即可作答．
【详解】若，则有a=b或者a=-b，
故命题是假命题；
逆命题为：若a=b，那么．
故答案为：假；若a=b，那么．
【点睛】考查了绝对值的意义以及命题与逆命题的知识，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么两个命题叫做互逆命题，其中一个叫命题，那另一个就称之为其逆命题．
14．小明和小杰在同一直道的A，B两点间作匀速往返走锻炼（忽略掉头等时间）．小明从A地出发，同时小杰从B地出发，两人第一次相遇时小明曾停下接电话数分钟．图中的折线表示从开始到小杰第一次到达A地止，两人之间的距离y（米）与行走时间x（分）的函数关系图象．则图中的________米，________分．
【答案】 3600 62.5
【分析】由折线统计图可知当两人相遇，时两人相遇，时，小明停下来，小杰一个人在走，时，两人都开始走，时，小明到达目的地，时，小明返回走，时，小杰到达目的地，两地相距4200米，据此即可得出答案．
【详解】解：由折线可知小杰的速度为：4200÷70=60米/分，
且有，解得c=30，
则两人速度和为米/分，故小明速度为：140-60=80米/分，
d点表示小明到达B地开始返向，
4200=30×80+（d-40）×80，
得d=62.5，
则a=62.5×60=3750，
b=3750-（80-60）×7.5=3600．
故答案为：3600，62.5．
【点睛】本题考查了一次函数的应用，理解函数图象上点的具体意义是本题的关键．
三、解答题
15．画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点D的对应点D′．
(1)根据要求画出平移后的△A′B′C′；
(2)画出BC边上的高AE，垂足为E；
(3)连接AA′、CC′，那么AA′与CC′的关系是 ；
(4)△A′B′C′的面积为 ．
【答案】(1)见解析
(2)见解析
(3)平行且相等
(4)3
【分析】（1）平移是将图形按照某个方向、距离移动，图形上所有点的移动方向、距离保持一致，由此即可画出平移图形；
（2）过一点作已知直线的垂线，根据尺规作图方法即可完成；
（3）根据平移的性质即可求出答案；
（4）用“割补法”即可求出答案．
（1）
解：平移后的△A′B′C′如图所示，
（2）
解：BC边上的高AE，垂足为E如图所示，
（3）
解：连接AA′、CC′如图所示，
根据平移的性质可知，，．
故答案是：平行且相等．
（4）
解：如图所示，
∴，，，，
∴，
故答案是：．
【点睛】本题主要考查图像的变换，根据平移的定义和性质，三角形的性质即可求出答案，掌握平移，三角形的面积公式是解题的关键．
16．如图，在△ABC中，AD是BC边上的高线，AD的垂直平分线分别交AB，AC于点E，F．
(1)若∠DAC＝20°，求∠FDC的度数；
(2)试判断∠B与∠AED的数量关系，并说明理由．
【答案】(1)70°
(2)∠AED＝2∠B，理由见解析
【分析】（1）根据垂直的定义得到∠ADC＝∠ADB＝90°，根据线段垂直平分线的性质得到AF＝DF，求得∠ADF＝∠DAF＝20°，于是得到∠FDC的度数；
（2）根据平行线的判定定理得到EFBC，根据平行线的性质定理得到∠AEF＝∠B，根据线段垂直平分线的性质得到AE＝DE，由等腰三角形的性质得到∠AEF＝∠DEF，于是得到结论．
（1）
解：∵AD⊥BC，
∴∠ADC＝∠ADB＝90°，
∵EF垂直平分AD，
∴AF＝DF，
∴∠ADF＝∠DAF＝20°，
∴∠FDC＝90°﹣20°＝70°；
（2）
∠AED＝2∠B，
理由：∵AD⊥BC，EF⊥AD，
∴EFBC，
∴∠AEF＝∠B，
∵EF垂直平分AD，
∴AE＝DE，
∴∠AEF＝∠DEF，
∴∠B＝∠AEF＝∠DEF，
∴∠AED＝2∠B．
【点睛】本题考查了线段垂直平分线的性质，等腰三角形的判定和性质，平行线的判定和性质，熟练掌握线段垂直平分线的性质是解题的关键．
17．已知y+3与x+2成正比例，且当x=3时，y=7．
(1)求y与x之间的函数解析式；
(2)当时，求y的值．
【答案】(1)
(2)
【分析】（1）根据题意设出解析式，待定系数法求解析式即可；
（2）将代入解析式进行计算即可．
（1）
解：设
∵当x=3时，y=7，
∴，
解得：；
∴，
整理得：；
（2）
解：当时：．
【点睛】本题考查求函数解析式，以及求函数值．正确的求出函数解析式是解题的关键．
18．如图，AD，AE分别是△ABC的角平分线和高线，∠B＝45°，∠C＝73°．
(1)求∠BAC的度数；
(2)求∠DAE的度数．
【答案】(1)
(2)
【分析】（1）根据三角形内角和定理求得即可；
（2）根据三角形的高的定义，求得，根据（1）的结论利用，即可求解．
（1）
解：∵∠B＝45°，∠C＝73°，
∴；
（2）
解：∵AD，AE分别是△ABC的角平分线和高线，
∴，，
∴．
【点睛】本题考查了三角形内角和定理，三角形的角平分线的定义，高的定义，掌握三角形内角和定理是解题的关键．
19．2020年“中国移动”公司提供两种通讯收费方案供客户选择．
方案一：按月收取座机费40元，此外每分钟的费用是0.1元；
方案二：无座机费用，直接按通话时间计费，每分钟的费用是0.2元．
根据以上信息，解答下列问题：
(1)设通话时间为分钟，方案一的通讯费用为元，方案二的通讯费用为元，则与的函数关系式为 ，与的函数关系式为 ．
(2)当通话时间为多少分钟时，两种方案费用相同？
(3)小明的爸爸每月的通话时间约为500分钟，则他选择哪种通讯收费方案更合算？
【答案】(1)，
(2)400分钟
(3)选择方案一收费方案更合算
【分析】（1）根据收费方式列式即可．
（2）将（1）中的结果等起来即可．
（3）把500分钟分别代入（1）中的两个式子得到结果比较大小即可．
（1）
解：根据题意得：
方案一：与的函数关系式为，
方案二：与的函数关系式为．
故答案为：，；
（2）
当时，则，
解得：，
答：当通话时间为400分钟时，两种方案费用相同；
（3）
当时，（元，
（元，
，
答：他选择方案一收费方案更合算．
【点睛】本题主要考查一次函数在方案选择上的应用，能够通过条件列出关系式是解题关键．
20．如图，△ABC中，∠A＝40°，∠B＝72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F．
(1)求∠ACE的度数；
(2)求∠CDF的度数．
【答案】(1)34°
(2)74°
【分析】（1）根据三角形的内角和定理求得∠ACB的度数，再根据CE平分∠ACB求得∠ACE的度数；
（2）根据三角形的外角的性质就可求得∠CED＝∠A+∠ACE，再结合CD⊥AB，DF⊥CE就可求解．
（1）
解：∵∠A＝40°，∠B＝72°，
∴∠ACB＝180°﹣40°﹣72°＝68°，
∵CE平分∠ACB，
∴∠ACE＝∠BCE＝34°；
（2）
解：∵∠CED＝∠A+∠ACE＝74°，
∴∠CDE＝90°，DF⊥CE，
∴∠CDF+∠ECD＝∠ECD+∠CED＝90°，
∴∠CDF＝∠CED＝74°．
【点睛】此题主要考查了三角形的内角和定理、三角形的外角的性质、以及角平分线定义和垂直定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
21．夏天到了，学校计划对一些班级和功能室装空调．根据调查，买2台A型空调和4台B型空调共需资金15000元，买5台A型空调和1台B型空调共需资金14100元．
(1)A型空调和B型空调的单价分别是多少元？
(2)学校共要买8台空调．要求资金不少于19000元且不多于19600元，请问有哪些购买方案？
【答案】(1)A型空调每台需2300元，B型空调每台需2600元
(2)有三种采购方案：方案一：采购4台A型空调，4台B型空调；方案二：采购5台A型空调，3台B型空调；方案三：采购6台A型空调，2台B型空调．
【分析】（1）根据“采购2台A型空调和4台B型空调，共需费用15000元；5台A型空调和1台B型空调，共需费用14100元”可以列出相应的方程组，从而可以解答本题；
（2）根据题意可以列出相应的不等式组，从而可以求得有几种采购方案．
（1）
解：设A型空调每台需x元，B型空调每台需y元．
由题意可列：，
解得，
答：A型空调每台需2300元，B型空调每台需2600元．
（2）
解：设采购A型空调m台，则采购B型空调（8-m）台，
由题意可列：，
解得，
∵m为正整数，
∴m=4，5，6．
∴有三种采购方案：
方案一：采购4台A型空调，4台B型空调；
方案二：采购5台A型空调，3台B型空调；
方案三：采购6台A型空调，2台B型空调．
【点睛】本题考查一元一次不等式组的应用、二元一次方程组的应用，解答本题的关键是找出相等或不等关系，利用方程和不等式解答．
22．定义：关于x的一次函数y＝ax+b与y＝bx+a（ab≠0）叫做一对交换函数，例如：一次函数y＝3x+4与y＝4x+3就是一对交换函数．
（1）一次函数y＝2x﹣b的交换函数是 ；
（2）当b≠﹣2时，（1）中两个函数图象交点的横坐标是 ；
（3）若（1）中两个函数图象与y轴围成的三角形的面积为4，求b的值．
【答案】（1）y＝﹣bx+2；（2）x＝1；（3）6或-10
【分析】（1）根据题目中的交换函数的定义进行求解，即可写出一次函数y＝2x﹣b的交换函数；
（2）根据题意和（1）中的结果，可以求得当b≠﹣2时，（1）中两个函数图象交点的横坐标；
（3）根据题意和（1）、（2）的结果，可以求得两函数图象与y轴的交点坐标及与y轴围成的三角形的高，则利用三角形面积公式建立关于b的方程，计算后即可得出b的值．
【详解】解：（1）由题意可得：
一次函数y＝2x﹣b的交换函数是y＝﹣bx+2，
故答案为：y＝﹣bx+2；
（2）当一次函数y＝2x﹣b与交换函数y＝﹣bx+2相交时，
则2x﹣b＝﹣bx+2，解得x＝1，
即当b≠﹣2时，（1）中两个函数图象交点的横坐标是x＝1，
故答案为：x＝1；
（3）函数y＝2x﹣b与y轴的交点是（0，﹣b），函数y＝﹣bx+2与y轴的交点为（0，2），
由（2）知，当b≠﹣2时，（1）中两个函数图象交点的横坐标是x＝1，
∵（1）中两个函数图象与y轴围成的三角形的面积为4，
∴＝4，
解得b＝6或b＝﹣10，
即b的值是6或﹣10．
【点睛】本题考查了一次函数的图象与性质、三角形的面积等知识，明确题意，熟练掌握一次函数的图象与性质是解答此题的关键．
23．如图，在平面直角坐标系中，已知，，三点，其中、、满足关系式，
(1)求、、的值；
(2)如果在第二象限内有一点，请用含的式子表示四边形的面积；
(3)在（2）的条件下，是否存在点，使四边形的面积与的面积相等？若存在，求出点的坐标；若不存在，请说明理由．
【答案】(1)，，
(2)
(3)存在，
【分析】（1）根据几个非负数和的性质得到，分别解一元一次方程得到；
（2）根据三角形的面积公式和四边形的面积= 进行计算；
（3）可求，是已知量，根据题意，列出方程求解即可．
（1）
由已知，
可得：
∴，，；
（2）
由（1）知，a=2，b=3，
∴A（0，2），B（3，0），
∴OA=2，OB=3，
，，
（3）
由（1）知，a=2，b=3，c=4，
∴A（0，2），B（3，0），C（3，4），
∴BC=4，
∴，
∵四边形ABOP的面积与△ABC的面积相等，
∴S=6，
由（2）知，S=m+3，
∴m+3=6，
∴m=3，
∴
【点睛】本题考查了坐标与图形性质：利用坐标计算线段的长度和判断线段与坐标轴的位置关系．也考查了三角形的面积公式．