【备战2024年中职高考】中职数学 一轮复习专题训练（考点讲与练）专题19 三角函数图象与性质（讲）.zip

这是一份【备战2024年中职高考】中职数学 一轮复习专题训练（考点讲与练）专题19 三角函数图象与性质（讲）.zip，文件包含备战2024年中职高考中职数学一轮复习之专题突破讲练测专题19三角函数图象与性质讲原卷版docx、备战2024年中职高考中职数学一轮复习之专题突破讲练测专题19三角函数图象与性质讲解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
一、考点要求
二、考点梳理
1.周期函数的定义及最小正周期
(1)周期函数的定义：
对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做周期函数．T叫做这个函数的周期．
(2)最小正周期：
如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期．
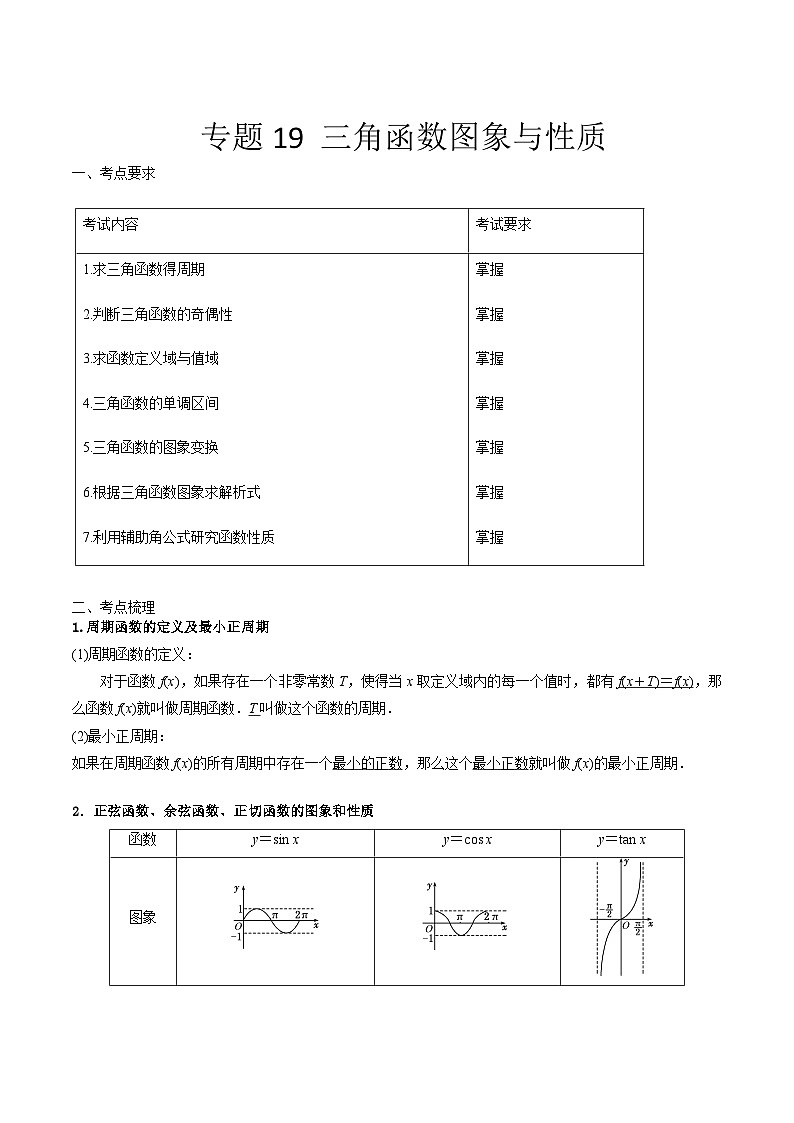
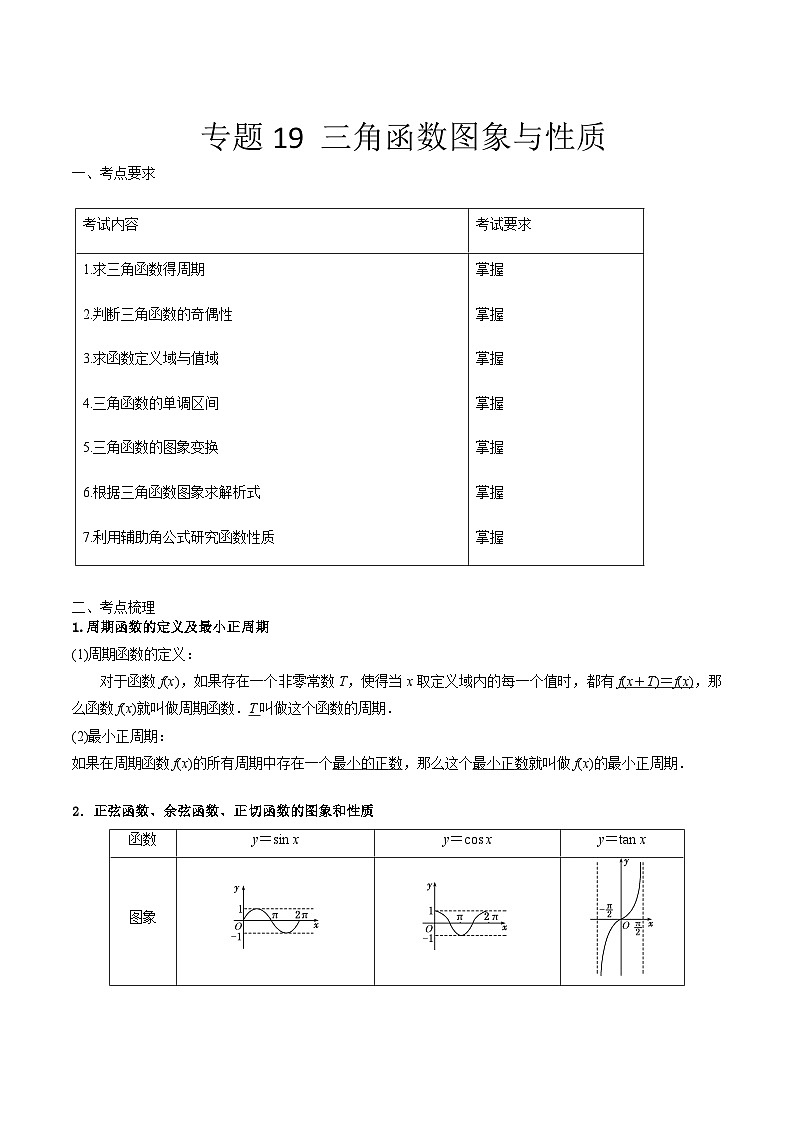
2．正弦函数、余弦函数、正切函数的图象和性质
3.五点作图法
函数在区间上的五个关键点是，
函数在区间上的五个关键点是
图像变换
函数的图象可由函数的图象经过如下变换得到：
（1）相位变换：，把图像上所有点向左
平移个单位
周期变换：，把上各点的横坐标伸长或缩短到原来的倍（纵坐标不变）
振幅变换：,把图象上各点纵坐标伸长
或缩短到原来的倍（横坐标不变）
5.初相、相位、最小正周期公式
当函数，表示一个振动量时，则叫做振幅，叫做周期，
叫做频率，叫做相位，叫做初相.函数
的最小正周期为
的最小正周期为
三、考点剖析
考点一 求三角函数的周期
【例1】下列四个函数中，周期为π的是（ ）
A．B．
C．D．
【变式练习】函数 的最小正周期是（ ）
A．B．
C．D．
【由题悟法】求周期性方法点拔：
(1)利用周期函数的定义；
(2)利用公式：y＝Asin(ωx＋φ)和y＝Acs(ωx＋φ)的最小正周期为eq \f(2π,|ω|)，y＝tan(ωx＋φ)的最小正周期为eq \f(π,|ω|)；
(3)利用图象．
周期性是函数的整体性质，要求对于函数整个定义域内的每一个x值都满足f(x＋T)＝f(x)，其中T是不为零的常数．如果只有个别的x值满足f(x＋T)＝f(x)，或找到哪怕只有一个x值不满足f(x＋T)＝f(x)，都不能说T是函数f(x)的周期．
考点二、判断三角函数的奇偶性
【例2】下列函数为偶函数的是（ ）
A．B．C．D．
【变式练习】若函数是奇函数，则可取的一个值为（ ）
A．B．C．D．
【由题悟法】首先要对函数的解析式进行恒等变换，再根据定义、诱导公式去判断所求三角函数的奇偶性；也可以根据图象做判断．
考点三 、求函数定义域与值域
【例3】函数y＝lg(sin x)＋eq \r(cs x－\f(1,2))的定义域为________
【例4】函数的值域是（ ）
A．B．
C．D．
【变式练习1】函数的值域是（ ）
A．B．C．D．
【变式练习2】函数在上的最小值为（ ）
A．－1B．C．D．
【由题悟法】
1．求三角函数定义域实际上是解简单的三角不等式，常借助三角函数线或三角函数图象来求解．
2．求解涉及三角函数的值域(最值)的题目一般常用以下方法：
(1)利用sin x、cs x的值域；
(2)形式复杂的函数应化为y＝Asin(ωx＋φ)＋k的形式逐步分析ωx＋φ的范围，根据正弦函数单调性写出函数的值域；
(3)换元法：把sin x或cs x看作一个整体，可化为求函数在给定区间上的值域(最值)问题.
考点四、求函数单调区间
【例5】函数的单调增区间是（ ）
A．B．
C．D．
【变式练习1】函数的递增区间为___________.
【变式练习2】函数的单调递增区间为______．
【由题悟法】求三角函数的单调区间时应注意以下几点：
(1)形如y＝Asin(ωx＋φ)(A>0，ω>0)的函数的单调区间，基本思路是把ωx＋φ看作是一个整体，由－eq \f(π,2)＋2kπ≤ωx＋φ≤eq \f(π,2)＋2kπ(k∈Z)求得函数的增区间，由eq \f(π,2)＋2kπ≤ωx＋φ≤eq \f(3π,2)＋2kπ(k∈Z)求得函数的减区间．
(2)形如y＝Asin(－ωx＋φ)(A>0，ω>0)的函数，可先利用诱导公式把x的系数变为正数，得到y＝－Asin(ωx－φ)，由－eq \f(π,2)＋2kπ≤ωx－φ≤eq \f(π,2)＋2kπ(k∈Z)得到函数的减区间，由eq \f(π,2)＋2kπ≤ωx－φ≤eq \f(3π,2)＋2kπ(k∈Z)得到函数的增区间．
(3)对于y＝Acs(ωx＋φ)，y＝Atan(ωx＋φ)等，函数的单调区间求法与y＝Asin(ωx＋φ)类似．
考点五、三角函数图象与变换
【例6】用五点作图法作y＝2sin4x的图象时，首先描出的五个点的横坐标是（ ）
A．0，，，，B．0，，，，
C．0，，，，D．0，，，，
【变式练习】用五点法作函数f(x)＝sin的图象时，所取的“五点”是（ ）
A．，，，，
B．，，，，
C．，，，，
D．，，，，
【例7】函数的图像向左平移个单位得到下列哪个函数（ ）
A．B．
C．D．
【变式练习】将函数的图象向左平移个单位长度，得到函数的图象，则（ ）
A．B．
C．D．
考点六、根据三角函数图象求解析式
【例8】已知的部分图象如图所示，则__________．
【变式练习1】函数的部分图象如图所示，则__，__，____.
【变式练习2】已知函数的一部分图象如图所示，如果，，．
(1)求函数的解析式；
(2)当时，求函数的取值范围．
考点七、.利用辅助角公式研究函数性质
【例9】设函数，则下列函数中为偶函数的是（ ）
A．B．C．D．
【变式练习1】已知．
(1)求的周期，最大值和最小值．
(2)把的图象向左平移后得到的图象，求的解析式．
【变式练习2】函数是（ ）
A．周期为的偶函数B．周期为的奇函数
C．周期为的偶函数D．周期为的奇函数
考试内容
考试要求
1.求三角函数得周期
2.判断三角函数的奇偶性
3.求函数定义域与值域
4.三角函数的单调区间
5.三角函数的图象变换
6.根据三角函数图象求解析式
7.利用辅助角公式研究函数性质
掌握
掌握
掌握
掌握
掌握
掌握
掌握
函数
y＝sin x
y＝cs x
y＝tan x
图象
定义域
R
R
eq \b\lc\{\rc\ (\a\vs4\al\c1(xx∈R且x≠))eq \f(π,2)＋kπ，k∈Z
值域
[－1,1]
[－1,1]
R
单调性
eq \b\lc\[\rc\ (\a\vs4\al\c1(2kπ－\f(π,2)，\f(π,2)＋))
2kπ(k∈Z)上递增；eq \b\lc\[\rc\ (\a\vs4\al\c1(2kπ＋\f(π,2)，\f(3π,2)＋))
2kπ(k∈Z)上递减
[2kπ－π，2kπ](k∈Z)上递增；[2kπ，2kπ＋π](k∈Z)上递减
eq \b\lc\(\rc\ (\a\vs4\al\c1(kπ－\f(π,2)，\f(π,2)＋))
kπ(k∈Z)上递增
最值
x＝eq \f(π,2)＋2kπ(k∈Z)时，ymax＝1；x＝－eq \f(π,2)＋2kπ(k∈Z)时，ymin＝－1
x＝2kπ(k∈Z)时，ymax＝1；x＝π＋2kπ(k∈Z)时，ymin＝－1
奇偶性
奇函数
偶函数
奇函数
对称
中心
(kπ，0)(k∈Z)
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋kπ，0))
(k∈Z)
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)，0))(k∈Z)
对称轴
方程
x＝eq \f(π,2)＋kπ(k∈Z)
x＝kπ(k∈Z)
周期
2π
2π
π