



- 【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题19 三角函数图象与性质(讲).zip 试卷 1 次下载
- 【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题20 正弦定理和余弦定理 (练).zip 试卷 0 次下载
- 【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题21 数列的概念与表示(练).zip 试卷 2 次下载
- 【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题21 数列的概念与表示(讲).zip 试卷 1 次下载
- 【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题22 等差数列与前n项和(练).zip 试卷 1 次下载
【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题20 正弦定理和余弦定理 (讲).zip
展开一、考点要求
二、考点梳理
1、三角形有关性质
(1)在△ABC中,A+B+C=;a+bc,a-b
(2)三角形面积公式:S△ABC=eq \f(1,2)ah=eq \f(1,2)absin C=eq \f(1,2)acsin B= ;
(3)在三角形中有:sin 2A=sin 2B⇔A=B或⇔三角形为等腰或直角三角形;
sin(A+B)=sin C,,sin eq \f(A+B,2)=cs eq \f(C,2).
2.正弦定理和余弦定理
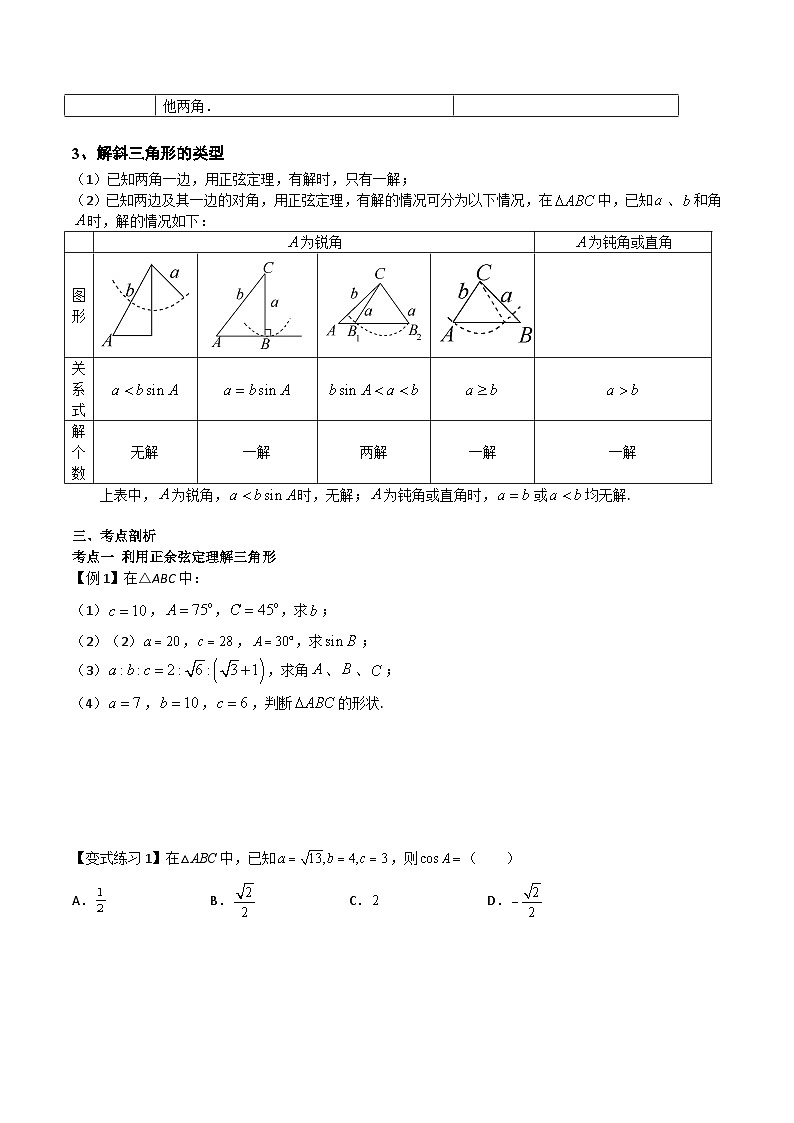
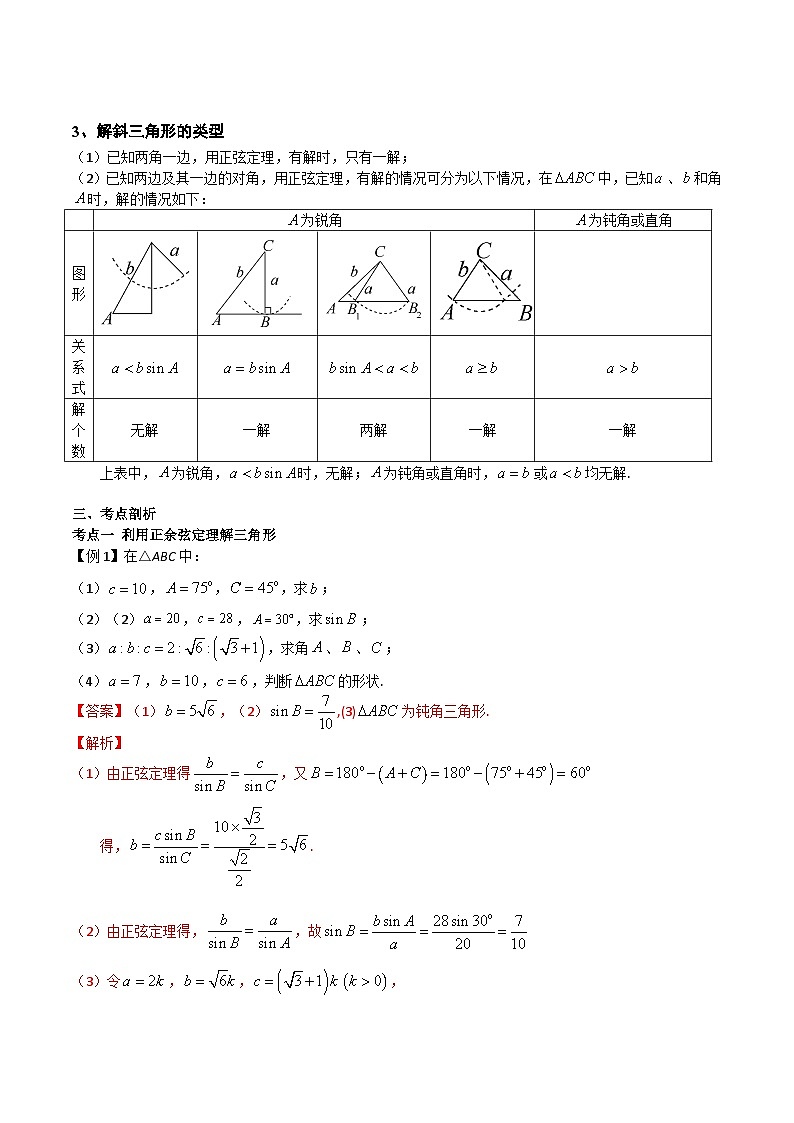
3、解斜三角形的类型
(1)已知两角一边,用正弦定理,有解时,只有一解;
(2)已知两边及其一边的对角,用正弦定理,有解的情况可分为以下情况,在中,已知、和角时,解的情况如下:
上表中,为锐角,时,无解;为钝角或直角时,或均无解.
三、考点剖析
考点一 利用正余弦定理解三角形
【例1】在△ABC中:
,,,求;
(2),,,求;
(3),求角、、;
(4),,,判断的形状.
【答案】(1),(2),(3)为钝角三角形.
【解析】
(1)由正弦定理得,又
得,.
(2)由正弦定理得,,故
(3)令,,,
由余弦定理的推论得
,同理,,,,.
(4), 最大
由余弦定理的推论得
, 为钝角三角形.
【变式练习1】在△ABC中,已知,则( )
A.B.C.D.
【答案】A
【解析】在△ABC中,已知,,,由余弦定理得:,
故选:A
【变式练习2】记△ABC的内角,,的对边分别为,,,若,,,则( )
A.2B.4C.6D.8
【答案】D
【解析】根据正弦定理有,得; 故选:D.
【由题悟法】在解三角形时,常常将正弦定理、余弦定理结合在一起使用,要注意恰当地选取定理,简化运算过程,提高解题速度,同时要挖掘题目中的隐含条件.解题时,要综合、灵活地运用两个定理,认真分析已知条件,选择需要先解的三角形和相关定理,并结合三角形的有关性质,如大边对大角、内角和定理等.注意数形结合,正确地求解三角形,防止出现漏解或增解的情况.
考点二、三角形解的情况的判定
【例2】在△ABC中,内角,,的对边分别为,,.已知,,,则此三角形的解的情况是( )
A.有一解B.有两解C.无解D.有解但解的个数不确定
【答案】C
【解析】由正弦定理可得可得,所以无解,所以三角形的解的情况是无解,故选:C.
【例3】不解三角形,判断下列三角形解的个数
(1),,; (2),, ;
(3),,; (4),,.
【解析】(1)唯一解,(2)无解,(3)两解,(4)两解
(1),且为钝角, 有唯一解;
(2),且为钝角, 有无解;
(3), , 有两解;
(4),又,故有两解.
【变式练习】在△ABC中,a=18,b=24,∠A=45°,此三角形解的情况为( )
A.一个解B.二个解C.无解D.无法确定
【答案】B
【解析】因为,如图所示:
所以,即,所以三角形解的情况为二个解. 故选:B
【由题悟法】
方法总结:已知三角形的两边和其中一边的对角,由正弦定理可以求出另一边的对角的正弦值,从而解出三角形,但这个三角形不一定有解.这类问题可以通过计算来判断,也可以通过画图用几何方法来判断.讨论时应注意两点:一是其正弦值与“1”的大小关系,从而决定符合正弦值的角是否存在;二是由此确定的角有几个,它与已知角的和是否小于.
考点三 、三角形形状的判定
【例4】在中,,试判断三角形的形状.
【答案】直角三角形
【解析】由余弦定理代入已知条件得,
整理,得,
即,,即或
根据勾股定理知是直角三角形.
【变式练习1】已知的内角A、B、C的对边分别为a、b、c,,则一定为_____三角形.
【答案】等腰
【解析】因为,由正弦定理可得,即,故一定为等腰三角形.
故答案为:等腰.
【变式练习2】在中,,则三角形的形状为( )
A.直角三角形B.等腰三角形或直角三角形
C.正三角形D.等腰三角形
【答案】A
【解析】中,,则,整理得,则,
则的形状为直角三角形,故选:A.
【由题悟法】
依据已知条件中的边角关系判断三角形的形状时,主要有如下两种方法:
(1)利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;
(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.
考点四、求三角形面积
【例5】在中,,,,则的面积等于______.
【答案】
【解析】在中,由余弦定理得:
,解得:,
所以的面积为:.故答案为:.
【变式练习1】在中,有.
(1)求角的大小;
(2)若,求的面积.
【答案】(1) (2)
【解析】(1)解:由题意可得,,故.
(2)解:由三角形的面积公式可得.因此,的面积为.
【变式练习2】在中,内角所对的边长分别为,且满足.
(1)求;
(2)若,求.
【答案】(1) (2)
【解析】(1)因为,由正弦定理可得,
因为,所以,因为为三角形的内角,所以
(2)因为,,,由正弦定理可得:,所以
因为为三角形的内角,所以,.
【由题悟法】求三角形面积一般步骤如下:
第一步 利用正、余弦定理求出三角形的基本元素如角与边
第二步 结合三角形的面积公式直接计算其面积
考点五、 正、余弦定理与其他知识的综合应用
【例6】中,已知,.
(1)求的值;
(2)若,为的中点,求的长.
【答案】(1),(2)
【解析】(1),且,
(2)由(1)得,
由正弦定理得,即,解得.
在中,,,.
【变式练习1】已知的内角所对的边长分别为,且.
(1)求角的大小;
(2)求的值;
(3)求的值.
【答案】(1),(2),(3)
【解析】(1)在中,,,,
由余弦定理得,又因为,所以;
(2)在中,由(1)知,,,
由正弦定理可得;
(3)由知,所以角A为锐角,因为,所以,
所以,,
所以.
【由题悟法】正、余弦定理与三角函数、平面向量综合考查出现频率较高.解决此类问题首先要把握题目重点考查知识点是什么,它们之间有怎样的联系,怎样将他们整合在一起,然后,将问题合理转化,特别注意三角形中角范围的限制.
考试内容
考试要求
1.利用正余弦定理解三角形
2.判断三角形形状
3.由余弦定理求角的大小
4.求三角形面积
掌握
掌握
掌握
掌握
定理
正弦定理
余弦定理
内容
变形
形式
= 1 \* GB3 ①,,;
②,,;
③;
④.
;
;
解决
的问题
①已知两角和任一边,求另一角和其他两条边.
②已知两边和其中一边的对角,求另一边和其他两角.
①已知三边,求各角;
②已知两边和它们的夹角,求第三边和其他两个角.
为锐角
为钝角或直角
图
形
关系式
解个数
无解
一解
两解
一解
一解
【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题39 概率(讲).zip: 这是一份【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题39 概率(讲).zip,文件包含备战2024年中职高考中职数学一轮复习之专题突破讲练测专题39概率讲原卷版docx、备战2024年中职高考中职数学一轮复习之专题突破讲练测专题39概率讲解析版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题30 椭圆(讲).zip: 这是一份【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题30 椭圆(讲).zip,文件包含备战2024年中职高考中职数学一轮复习之专题突破讲练测专题30椭圆讲原卷版docx、备战2024年中职高考中职数学一轮复习之专题突破讲练测专题30椭圆讲解析版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题28 圆 (讲).zip: 这是一份【备战2024年中职高考】中职数学 一轮复习专题训练(考点讲与练)专题28 圆 (讲).zip,文件包含备战2024年中职高考中职数学一轮复习之专题突破讲练测专题28圆讲原卷版docx、备战2024年中职高考中职数学一轮复习之专题突破讲练测专题28圆讲解析版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。












