【备战2024年中职高考】中职数学 二轮复习 专题训练 专题26 圆-练习

这是一份【备战2024年中职高考】中职数学 二轮复习 专题训练 专题26 圆-练习，共10页。试卷主要包含了 圆的定义及方程，点与圆的位置关系，圆与圆的位置关系，求圆的方程的两种方法，圆的面积， 圆C1等内容，欢迎下载使用。

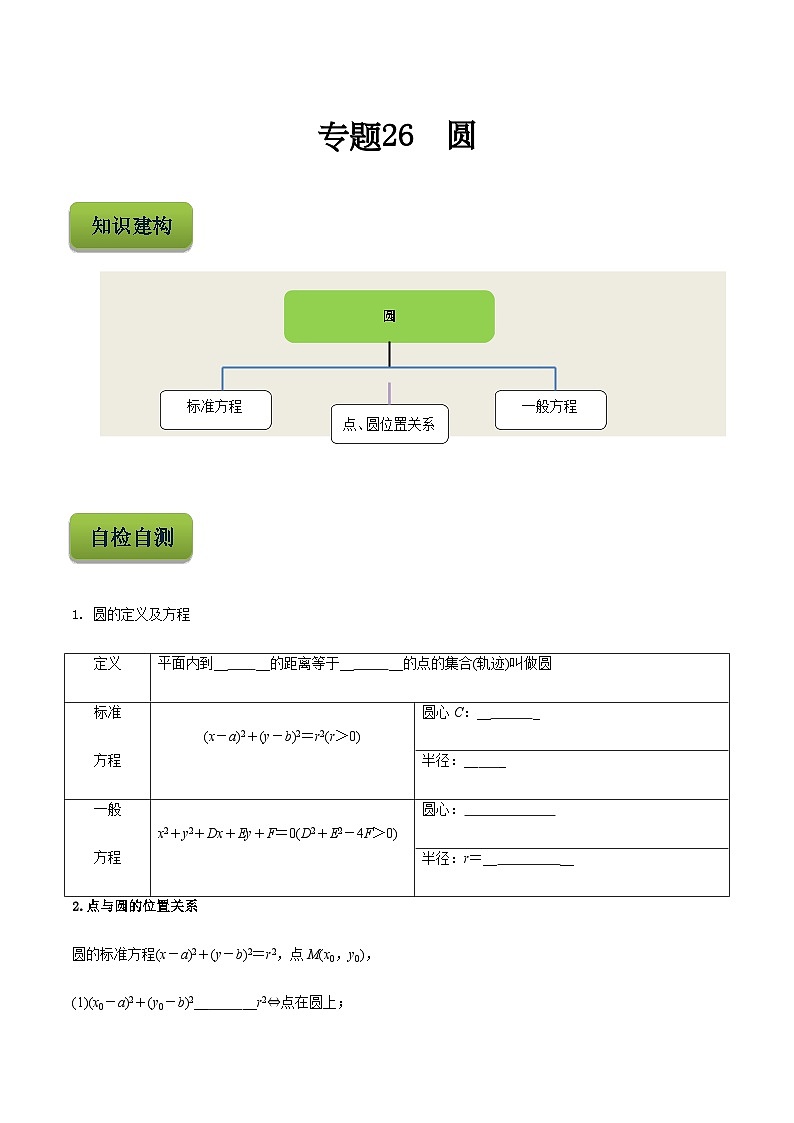
圆
标准方程
一般方程
点、圆位置关系
自检自测
1. 圆的定义及方程
2.点与圆的位置关系
圆的标准方程(x－a)2＋(y－b)2＝r2，点M(x0，y0)，
(1)(x0－a)2＋(y0－b)2__ __r2⇔点在圆上；
(2)(x0－a)2＋(y0－b)2__ __r2⇔点在圆外；
(3)(x0－a)2＋(y0－b)2__ __r2⇔点在圆内．
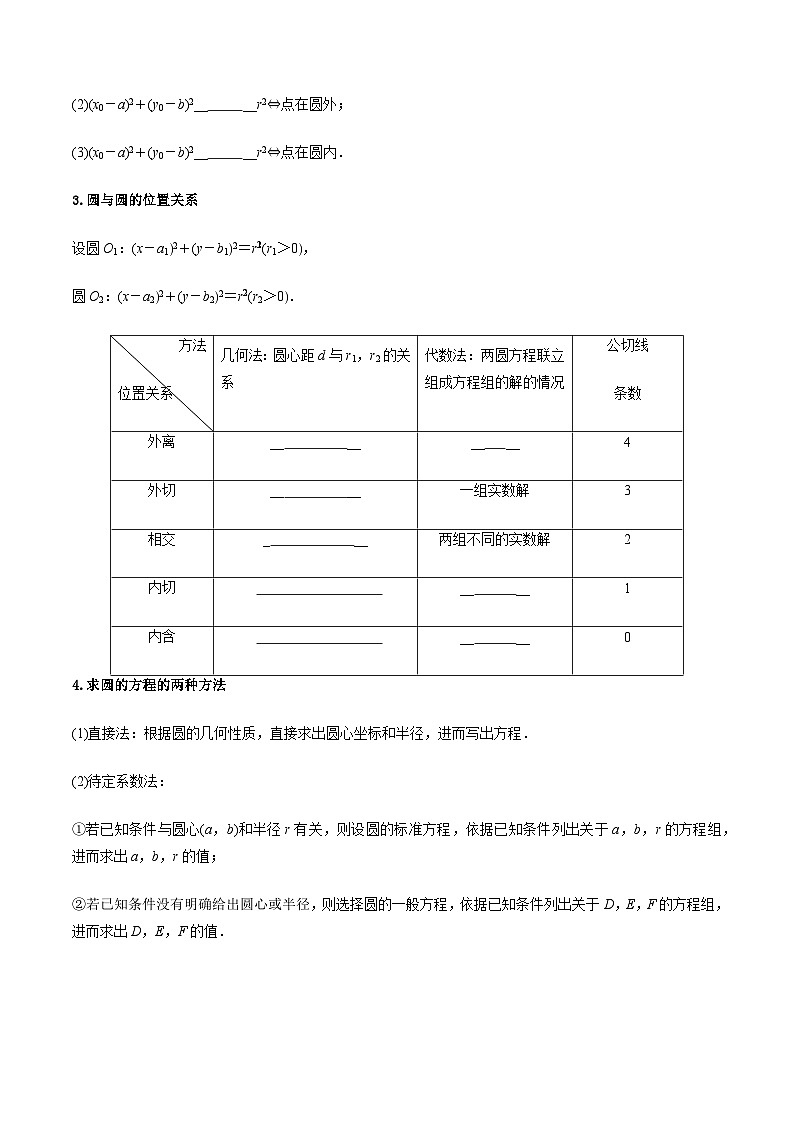
3.圆与圆的位置关系
设圆O1：(x－a12＋(y－b12＝req \\al(2,1)(r1＞0，
圆O2：(x－a22＋(y－b22＝req \\al(2,2)(r2＞0．
4.求圆的方程的两种方法
(1)直接法：根据圆的几何性质，直接求出圆心坐标和半径，进而写出方程．
(2)待定系数法：
①若已知条件与圆心(a，b)和半径r有关，则设圆的标准方程，依据已知条件列出关于a，b，r的方程组，进而求出a，b，r的值；
②若已知条件没有明确给出圆心或半径，则选择圆的一般方程，依据已知条件列出关于D，E，F的方程组，进而求出D，E，F的值．
5.圆的面积：S圆 = , 圆的周长C =
常见题型
6.圆的一般式化成标准式方程用配方法:配一次项系数一半的平方.
1. 求圆的方程
2. 求圆的圆心、半径
实战突破
3.判断点、圆，圆、圆之间位置关系
一．选择题：本大题共 18小题，每小题4 分，满分 72 分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知圆的方程为(x − 3)2 + (y + 1)2 = 4，则圆心坐标和半径分别为（ ）
A.(−3,1)2B.(3, −1) 2
C. (−3,1)4D. (3, −1) 4
2. 圆x2 + y2 + 10x − 6y = 0的圆心坐标为()
A.(0,4)B.(5, −3)
C.(−5,3)D.(4,0)
3. 已知圆C:x2 + y2 − 4x + 2y + 3 = 0,则圆C 的面积为 ( )
A.2πB.2√2π
C.4π D.8π
4. 已知圆x2 + y2 + 2mx + 2y = 0的半径是 1，则圆心坐标为()
A.(0, −1)B.(1, −1)
C.(−1,0)D.(−1,1)
5. 若直线l:y=2x+1 过圆C：x2 + y2 + ax + 2y = 0的圆心，则a= ( )
A.2B.
C.−1D.0
6. 点A(1, −3)在圆(x − 3)2 + (y − 2)2 = 9的( )
A.内部B.外部
C.圆上D.无法判断
7. 若抛物线y = x2 + a(1 − 2x) + a2 + 1的顶点在圆x2 + y2 = 5的内部，则a 的取值范围为区间( ) A.(−2,2) B.(−1,1)
C.(−2,1) D.(−1,2)
8. 圆x2 + y2 − 2x + 2y = 0的圆心到直线2x + 3y + m = 0的距离为√13，则m 的值是（ ）
A.−12B.14
C.−12 或 14D. 12 或− 14
9. 两圆x2 + y2 = 1和x2 + (y − 3)2 = 1的位置关系是 （ ）
A.相交 B.相离
C.外切D.内切
10. 圆C1: x2 + y2 + 2x − 2y + 1 = 0和C2: x2 + y2 + 4x − 5 = 0的位置关系是( )
A.外离B.外切
C.相交D.内含
11. 要使圆x2 + y2 = r2(r > 0)与圆(x − 3)2 + (y − 4)2 = 4有交点，则r 的取值范围是（ ）
A.0 < r ≤ 5 B.2 ≤ r ≤ 7
C.3 ≤ r ≤ 7D.3 ≤ r ≤ 9
12. 设线段PQ 是以点C（1,1）为圆心的圆的一条直径，已知点P 的坐标为(3, −1)，则点Q 的坐标为（ ） A.(−2,2) B.(2,0)
C.(−1,2) D.(−1,3)
13. 长为2的线段MN的两个端点分别在x轴、y轴上滑动，则线段MN 的中点的轨迹方程是( )
A.x2 + y2 = 2B. x2 + y2 = 4
C. x2 + y2 = √2D. x2 + y2 = 1
14. 过点A(1, −1), B(2,0), C(0,0)的圆的方程是 ( )
A.x2 + (y − 1)2 = 1B.(x − 1)2 + y2 = 1
C. (x + 1)2 + y2 = 1D. x2 + (y + 1)2 = 1
15. 圆心在直线2x − y + 6 = 0上,半径为 2,且与x 轴相切的圆的标准方程为()
A.(x − 2)2 + (y + 2)2 = 4B. (x + 2)2 + (y − 2)2 = 4和(x + 4)2 + (y + 2)2 = 4
C.(x + 2)2 + (y − 2)2 = 4D. (x + 4)2 + (y + 2)2 = 4和(x + 4)2 + (y − 2)2 = 4
16. 若直线ax＋by＝1与圆x2＋y2＝1相交，则P(a，b)与圆x2＋y2＝1的关系为( )
A．在圆上 B．在圆外
C．在圆内 D．以上都有可能
17. 圆x2＋y2－2x－8y＋13＝0的圆心到直线ax＋y－1＝0的距离为1，则a＝( )
A．－eq \f(4,3) B．－eq \f(3,4)
C．eq \r(3) D．2
18. 圆心为(2,1)且和x轴相切的圆的方程是( )
A．(x－2)2＋(y－1)2＝1 B．(x＋2)2＋(y＋1)2＝1
C．(x－2)2＋(y－1)2＝5 D．(x＋2)2＋(y＋1)2＝5
二.填空题：本大题共7小题，每小题4分，满分 28 分.
19. 圆心在直线x－2y－3＝0上，且过点A(2，－3)，B(－2，－5)的圆的方程为__ __．
20. 已知圆C经过A(5,1)，B(1,3)两点，圆心在x轴上，则C的方程为 .
21. 圆x2 + y2 − 6y + m = 0的半径为 2,则m 的值等于__ __.
22. 圆心为A(2, −1)且过B(−1,3)的圆的方程为__ __.
23. 已知点A(5,2))和B(−1,4)，则以AB 为直径的圆的方程是__ _.
24. 圆x2 − 4x + y2 = 0的圆心到直线x +y − 4 = 0的距离为__ __．
25. 已知直角三角形的顶点A(−4,4)，B(-1,7)和C(2,4)，则该三角形外接圆的方程是__ .
自检自测
专题24 直线的方程 (参考答案)
1. 圆的定义及方程
2.点与圆的位置关系
圆的标准方程(x－a)2＋(y－b)2＝r2，点M(x0，y0)，
(1)(x0－a)2＋(y0－b)2__＝__r2⇔点在圆上；
(2)(x0－a)2＋(y0－b)2__＞__r2⇔点在圆外；
(3)(x0－a)2＋(y0－b)2__＜__r2⇔点在圆内．
3.圆与圆的位置关系
设圆O1：(x－a12＋(y－b12＝req \\al(2,1)(r1＞0，
圆O2：(x－a22＋(y－b22＝req \\al(2,2)(r2＞0．
4.求圆的方程的两种方法
(1)直接法：根据圆的几何性质，直接求出圆心坐标和半径，进而写出方程．
(2)待定系数法：
①若已知条件与圆心(a，b)和半径r有关，则设圆的标准方程，依据已知条件列出关于a，b，r的方程组，进而求出a，b，r的值；
②若已知条件没有明确给出圆心或半径，则选择圆的一般方程，依据已知条件列出关于D，E，F的方程组，进而求出D，E，F的值．
5.圆的面积：S圆 = πr2, 圆的周长C = 2πr
6.圆的一般式化成标准式方程用配方法:配一次项系数一半的平方.
实战突破
定义
平面内到__ __的距离等于__ __的点的集合(轨迹)叫做圆
标准
方程
(x－a)2＋(y－b)2＝r2(r＞0)
圆心C：__ _
半径：__ _
一般
方程
x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F＞0)
圆心：
半径：r＝__ __
方法
位置关系
几何法：圆心距d与r1，r2的关系
代数法：两圆方程联立组成方程组的解的情况
公切线
条数
外离
__ __
__ __
4
外切
__ __
一组实数解
3
相交
_ __
两组不同的实数解
2
内切

__ __
1
内含

__ __
0
定义
平面内到__定点__的距离等于__定长__的点的集合(轨迹)叫做圆
标准
方程
(x－a)2＋(y－b)2＝r2(r＞0)
圆心C：__(a，b)__
半径：__r__
一般
方程
x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F＞0)
圆心：eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(D,2)，－\f(E,2)))
半径：r＝__eq \f(\r(D2＋E2－4F),2)__
方法
位置关系
几何法：圆心距d与r1，r2的关系
代数法：两圆方程联立组成方程组的解的情况
公切线
条数
外离
__d＞r1＋r2__
__无解__
4
外切
__d＝r1＋r2__
一组实数解
3
相交
__|r1－r2|＜d＜r1＋r2__
两组不同的实数解
2
内切
d＝|r1－r2|(r1≠r2
__一组实数解__
1
内含
0≤d＜|r1－r2|(r1≠r2
__无解__
0
1
2
3
4
5
6
7
8
9
10
11
12
13
答案
B
C
A
A
A
B
C
C
B
D
C
D
D
题号
14
15
16
17
18
答案
B
B
B
A
A
题号
19
20
21
22
答案
(x＋1)2＋(y＋2)2＝10
(x－2)2＋y2＝10
5
(x − 2)2+ (y + 1)2 = 25
题号
23
24
25
(x − 2)2 + (y -3)2= 10
1
(x + 1)2+ (y − 4)2 = 9