



高中数学人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示优质课ppt课件
展开平面向量基本定理:如果两向量a,b不共线,那么对于平面中 任意向量p,都存在唯一确定的有序数对{x,y},使 p=xa+yb.
当a⊥b,且a,b都是单位向量时,这种分解叫做单位正交分解,(x,y)即为p的坐标
当a⊥b时,这种分解叫做正交分解
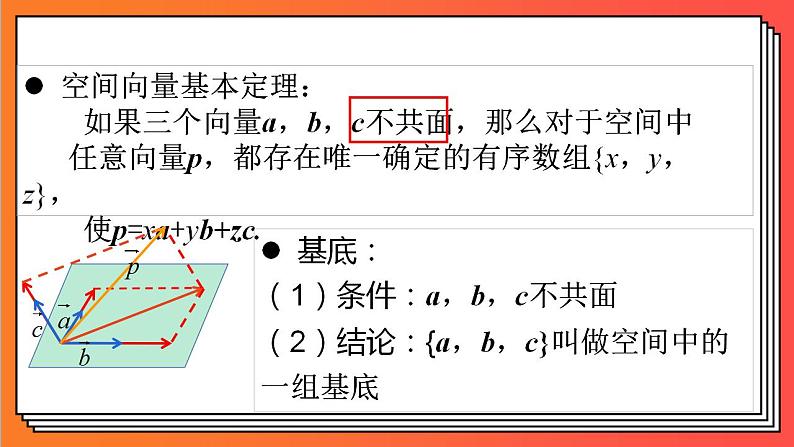
空间向量基本定理:如果三个向量a,b,c不共面,那么对于空间中 任意向量p,都存在唯一确定的有序数组{x,y,z},使p=xa+yb+zc.
基底:(1)条件:a,b,c不共面(2)结论:{a,b,c}叫做空间中的一组基底
当a、b、c两两垂直时,这种分解叫做正交分解
当a、b、c两两垂直且为单位向量时,这种分解叫做单位正交分解,p=xa+yb+zc,此时,(x,y,z)即为p的坐标
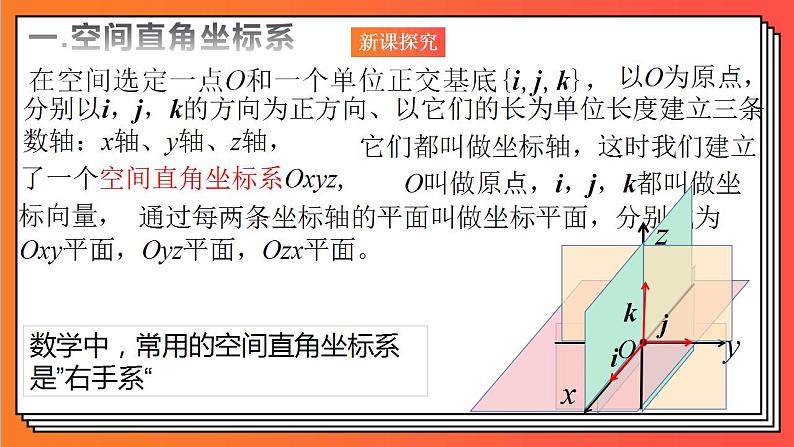
在空间选定一点O和一个单位正交基底{i,j,k},
以O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,
它们都叫做坐标轴,这时我们建立了一个空间直角坐标系Oxyz,
O叫做原点,i,j,k都叫做坐标向量,
通过每两条坐标轴的平面叫做坐标平面,分别成为Oxy平面,Oyz平面,Ozx平面。
数学中,常用的空间直角坐标系是”右手系“
二.空间向量的坐标表示
空间中一点M的坐标:用有序实数对(x,y,z)表示。x→横坐标y→纵坐标z→竖坐标
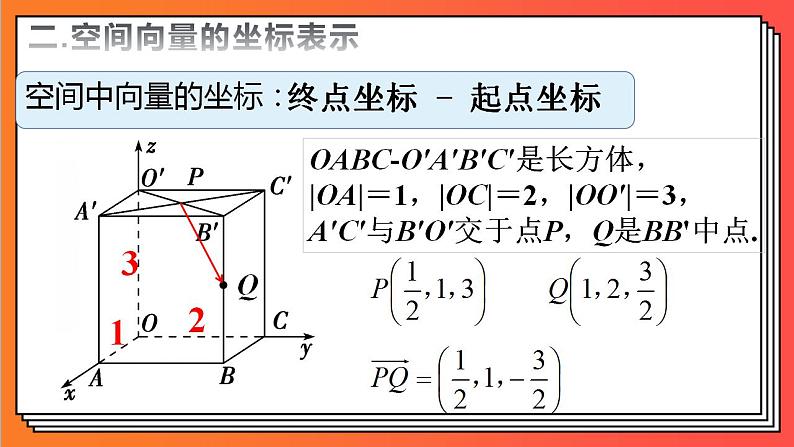
OABCO′A′B′C′是长方体,|OA|=1,|OC|=2,|OO′|=3,A′C′与B′O′交于点P,Q是BB'中点.
终点坐标 - 起点坐标
三.空间直角坐标系中对称点的坐标
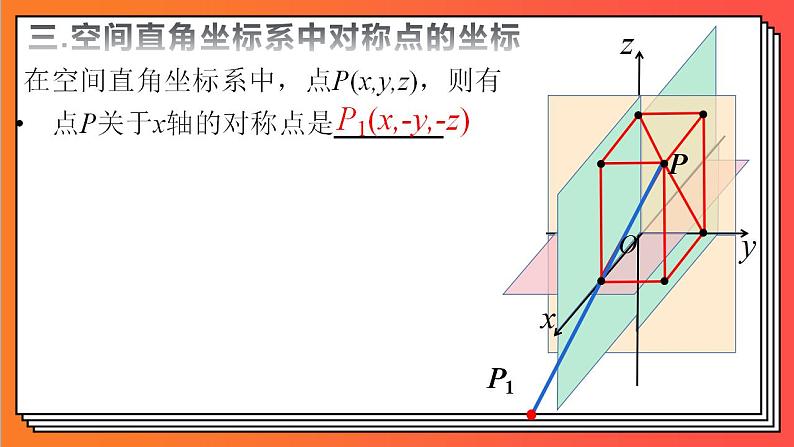
在空间直角坐标系中,点P(x,y,z),则有
点P关于x轴的对称点是_______
P1(x,-y,-z)
点P关于y轴的对称点是_______
P2(-x,y,-z)
点P关于z轴的对称点是_______
P3(-x,-y,z)
点P关于原点的对称点是_______
P4(-x,-y,-z)
点P关于平面xOy的对称点是_______
点P关于平面xOz的对称点是_______
点P关于平面yOz的对称点是_______
(1)下列空间直角坐标系中,是右手直角坐标系的是______
(2)如图,已知在三棱锥A-BCD中,AB⊥底面BCD,BC⊥BD,请叙述如何建立空间直角坐标系。
解:因为AB⊥底面BCD,所以AB⊥BC,AB⊥BD。又因为BC⊥BD,所以以点B为坐标原点,以DB所在直线为x轴,BC所在直线为y轴,BA所在直线为z轴,建立空间直角坐标系。
例2 空间直角坐标系中点的坐标表示
(1)如图所示,正方体ABCD-A1B1C1D1的棱长为1,则点B1的坐标是()
A.(1,0,0)B.(1,0,1)C.(1,1,1)D.(1,1,0)
(2)(多选)在空间直角坐标系中,点P(1,-3,2)在坐标平面内的射影可能为()
A.(-1,3,-2)B.(1,-3,0)C.(0,-3,2)D.(1,0,2)
A.原点B.x轴C.y轴D.z轴
(3)在空间直角坐标系中,点A(1,-2,3)与点B(-1,-2,-3)关于()对称
例3 空间向量的坐标表示
高中人教A版 (2019)第一章 空间向量与立体几何1.3 空间向量及其运算的坐标表示获奖作业ppt课件: 这是一份高中人教A版 (2019)<a href="/sx/tb_c4000322_t3/?tag_id=26" target="_blank">第一章 空间向量与立体几何1.3 空间向量及其运算的坐标表示获奖作业ppt课件</a>,文件包含131《空间直角坐标系》课件-人教版高中数学选修一pptx、131《空间直角坐标系》分层作业原卷版-人教版高中数学选修一docx、131《空间直角坐标系》分层作业解析版-人教版高中数学选修一docx等3份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
数学选择性必修 第一册1.3 空间向量及其运算的坐标表示授课课件ppt: 这是一份数学选择性必修 第一册1.3 空间向量及其运算的坐标表示授课课件ppt,共33页。
人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示优秀ppt课件: 这是一份人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示优秀ppt课件,共23页。PPT课件主要包含了一空间直角坐标系,二空间一点的坐标,三空间向量的坐标,即时巩固,求空间点的坐标,答案不唯一,反思感悟,空间点的对称问题,空间向量的坐标等内容,欢迎下载使用。













