



所属成套资源:2023年高考数学真题专题汇编(新高考卷)
专题13 双曲线-2023年高考数学真题专题汇编(新高考卷)
展开
这是一份专题13 双曲线-2023年高考数学真题专题汇编(新高考卷),文件包含专题13双曲线原卷版docx、专题13双曲线解析版docx等2份试卷配套教学资源,其中试卷共72页, 欢迎下载使用。
2023真题展现
考向一 双曲线的离心率
真题考查解读
近年真题对比
考向一 双曲线的渐近线方程
命题规律解密
名校模拟探源
易错易混速记/二级结论速记
考向一 双曲线的离心率
1.(2023•新高考Ⅰ•第16题)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2.点A在C上,点B在y轴上,F1A→⊥F1B→,F2A→=-23F2B→,则C的离心率为 .
【答案】355
解:(法一)如图,设F1(﹣c,0),F2(c,0),B(0,n),
设A(x,y),则F2A→=(x-c,y),F2B→=(-c,n),
又F2A→=-23F2B→,则x-c=23cy=-23n,可得A(53c,-23n),
又F1A→⊥F1B→,且F1A→=(83c,-23n),F1B→=(c,n),
则F1A→⋅F1B→=83c2-23n2=0,化简得n2=4c2.
又点A在C上,则259c2a2-49n2b2=1,整理可得25c29a2-4n29b2=1,
代n2=4c2,可得25c2a2-16c2b2=9,即25e2-16e2e2-1=9,
解得e2=95或15(舍去),
故e=355.
(法二)由F2A→=-23F2B→,得|F2A→||F2B→|=23,
设|F2A→|=2t,|F2B→|=3t,由对称性可得|F1B→|=3t,则|AF1→|=2t+2a,|AB→|=5t,
设∠F1AF2=θ,则sinθ=3t5t=35,所以csθ=45=2t+2a5t,解得t=a,
所以|AF1→|=2t+2a=4a,|AF2→|=2a,
在△AF1F2 中,由余弦定理可得csθ=16a2+4a2-4c216a2=45,
即5c2=9a2,则e=355.
【命题意图】
考查双曲线的定义、标准方程、几何性质、直线与双曲线.考查运算求解能力、逻辑推导能力、分析问题与解决问题的能力、数形结合思想、化归与转化思想.
【考查要点】
双曲线的定义、方程、性质是高考常考内容,以小题出现,常规题,难度中等.
【得分要点】
一、双曲线的定义
把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
注:1、集合语言表达式
双曲线就是下列点的集合:.常数要小于两个定点的距离.
2、对双曲线定义中限制条件的理解
(1)当||MF1|-|MF2||=2a>|F1F2|时,M的轨迹不存在.
(2)当||MF1|-|MF2||=2a=|F1F2|时,M的轨迹是分别以F1,F2为端点的两条射线.
(3)当||MF1|-|MF2||=0,即|MF1|=|MF2|时,M的轨迹是线段F1F2的垂直平分线.
(4)若将定义中的绝对值去掉,其余条件不变,则动点的轨迹为双曲线的一支.具体是哪一支,取决于与的大小.
①若,则,点的轨迹是靠近定点的那一支;
②若,则,点的轨迹是靠近定点的那一支.
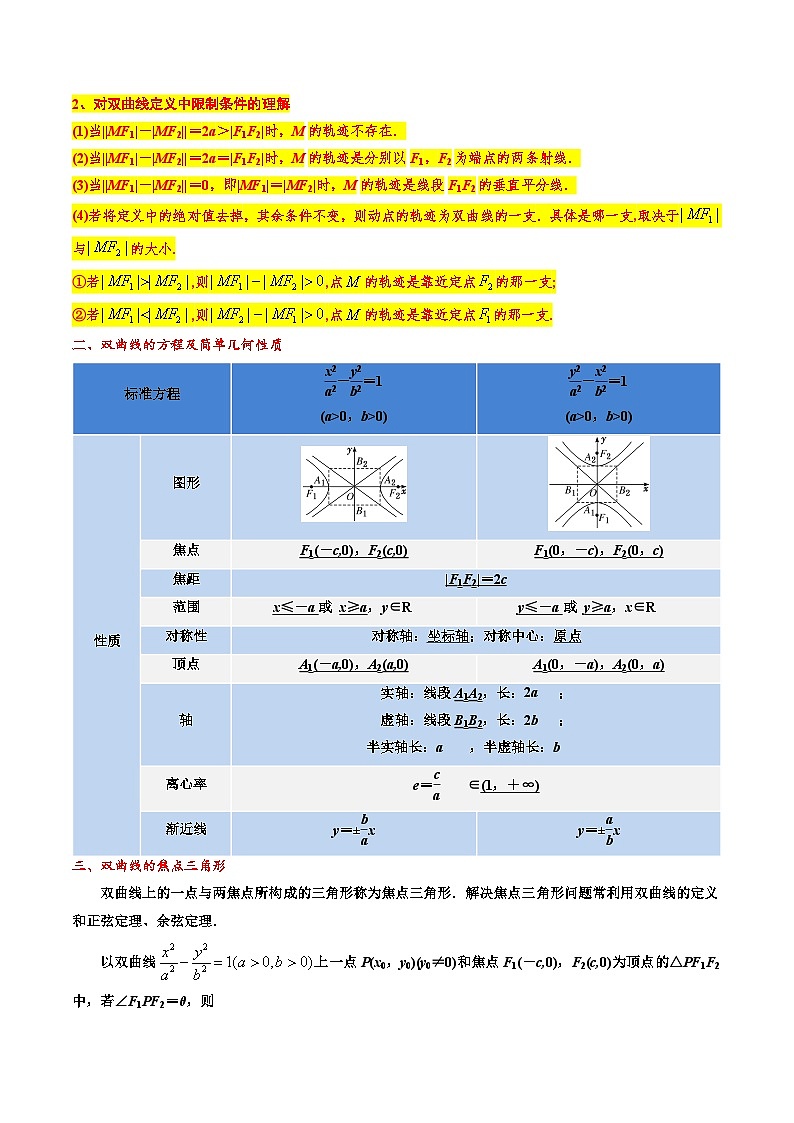
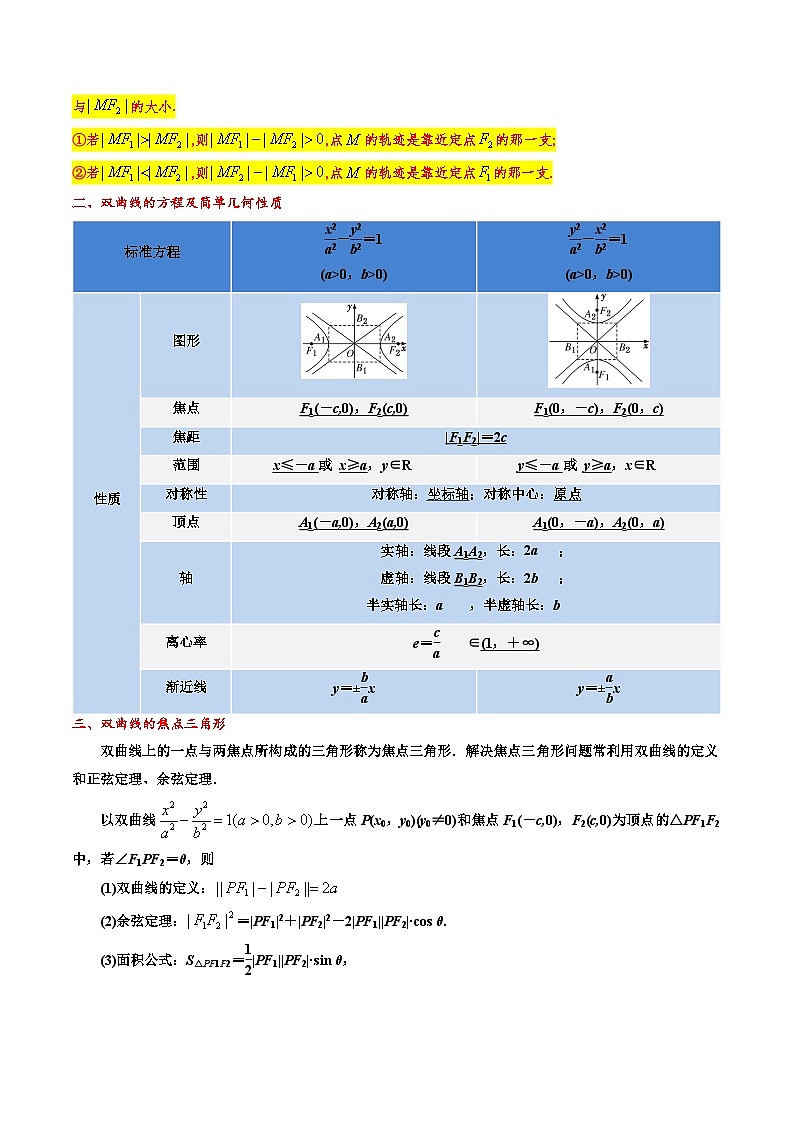
二、双曲线的方程及简单几何性质
三、双曲线的焦点三角形
双曲线上的一点与两焦点所构成的三角形称为焦点三角形.解决焦点三角形问题常利用双曲线的定义和正弦定理、余弦定理.
以双曲线上一点P(x0,y0)(y0≠0)和焦点F1(-c,0),F2(c,0)为顶点的△PF1F2中,若∠F1PF2=θ,则
(1)双曲线的定义:
(2)余弦定理:=|PF1|2+|PF2|2-2|PF1||PF2|·cs θ.
(3)面积公式:S△PF1F2=eq \f(1,2)|PF1||PF2|·sin θ,
重要结论:S△PF1F2=
推导过程:由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|·cs θ得
由三角形的面积公式可得
S△PF1F2=
=
四、直线与双曲线的位置关系
1、把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考察方程的判别式.
(1)Δ>0时,直线与双曲线有两个不同的公共点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ0,b>0)
eq \f(y2,a2)-eq \f(x2,b2)=1
(a>0,b>0)
性质
图形
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
焦距
|F1F2|=2c
范围
x≤-a或 x≥a,y∈eq \a\vs4\al(R)
y≤-a或 y≥a,x∈eq \a\vs4\al(R)
对称性
对称轴:坐标轴;对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
实轴:线段A1A2,长:eq \a\vs4\al(2a);
虚轴:线段B1B2,长:eq \a\vs4\al(2b);
半实轴长:eq \a\vs4\al(a),半虚轴长:eq \a\vs4\al(b)
离心率
e=eq \a\vs4\al(\f(c,a))∈(1,+∞)
渐近线
y=±eq \f(b,a)x
y=±eq \f(a,b)x
相关试卷
这是一份专题19 导数综合-2023年高考数学真题专题汇编(新高考卷),文件包含专题19导数综合原卷版docx、专题19导数综合解析版docx等2份试卷配套教学资源,其中试卷共122页, 欢迎下载使用。
这是一份专题17 概率-2023年高考数学真题专题汇编(新高考卷),文件包含专题17概率原卷版docx、专题17概率解析版docx等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。
这是一份专题16 统计-2023年高考数学真题专题汇编(新高考卷),文件包含专题16统计原卷版docx、专题16统计解析版docx等2份试卷配套教学资源,其中试卷共78页, 欢迎下载使用。








