高中数学1.1 直线拟合导学案

这是一份高中数学1.1 直线拟合导学案，共9页。

[教材要点]
要点一 直线拟合
1．散点图
每个点对应的一对数据(xi，yi)，称为成对数据．这些点构成的图称为散点图．
2．曲线拟合
从散点图上可以看出，如果变量之间存在着某种关系，这些点会有一个大致趋势，这种趋势通常可以用一条光滑的曲线来近似地描述．这样近似描述的过程称为曲线拟合．
3．直线拟合
若在两个变量X和Y的散点图中，所有点看上去都在一条________附近波动，此时就可以用一条________来近似地描述这两个量之间的关系，称之为直线拟合．
要点二 一元线性回归方程
1．最小二乘法
对于给定的两个变量X和Y，可以把其成对的观测值(x1，y1)，(x2，y2)，…，(xn，yn)表示为平面直角坐标系中的n个点．由直线方程Y＝a＋bX计算出来的值a＋bxi(x＝1，2，…n)，与实际观测值yi的差异尽可能小．换句话说，a，b的取值使[y1－(a＋bx1)]2＋[y2－(a2＋bx2)]2＋…＋[yn－(a＋bxn)]2达到最小．这个方法称为最小二乘法．
2．线性回归方程
直线方程Y＝________称作Y关于X的线性回归方程，相应的直线称作Y关于X的回归直线，，是这个线性回归方程的系数．其中
[基础自测]
1．思考辨析(正确的画“√”，错误的画“×”)
(1)利用散点图可以直观判断两个变量的关系是否可以用线性表示．( )
(2)线性回归方程适用于一切样本和总体．( )
(3)线性回归方程一般都有局限性．( )
(4)线性回归方程一定过样本中的某一点．( )
2．如果记录了x，y的几组数据分别为(0，1)，(1，3)，(2，5)，(3，7)，那么y关于x的线性回归直线必过点( )
A．(2，2) B．(1.5，2) C．(1，2) D．(1.5，4)
3．随机抽样中测得四个样本点为(1，2)，(2，3)，(3，4)，(4，5)，则y与x之间的线性回归方程为( )
A．y＝x＋1 B．y＝x＋2
C．y＝2x＋1 D．y＝x－1
4．已知变量x，y线性相关，由观测数据算得样本的平均数＝4，＝5，线性回归方程＝x＋中的系数，满足＋＝4，则线性回归方程为________．
题型一 一元线性回归方程的特性
例1 已知x，y的取值如下表：
由所给数据在散点图上的位置分析可知y与x线性相关，且线性回归方程为＝0.95x＋，则＝( )
A．1.45 B．1.55 C．1.65 D．1.80
方法归纳
(1)线性回归直线过点()，通过把()代入线性回归方程可求出线性回归方程的系数，以及列表中的参数，这是方程思想的应用，是求线性回归方程的逆向应用．
(2)＝x＋中，的实际意义是x每增加一个单位，y的平均变化量，的实际意义是不受x影响的部分．另外，当x＝m时应求得＝m＋，即x为m时的y的平均值．
跟踪训练1 某工厂某产品产量x(千件)与单位成本y(元)满足线性回归方程＝77.36－1.82x，则以下说法中正确的是( )
A．产量每增加1千件，单位成本约下降1.82元
B．产量每减少1千件，单位成本约下降1.82元
C．当产量为1千件时，单位成本为75.54元
D．当产量为2千件时，单位成本为73.72元
题型二 求线性回归方程
例2 某种产品的广告费用支出x(单位：百万元)与销售额y(单位：百万元)之间有如下的对应数据：
(1)画出散点图；
(2)求线性回归方程；
(3)试预测广告费用支出为10百万元时，销售额是多少．
(参考数据：＝145，＝1 380)
状元随笔 注意线性回归方程中的一次项系数为，常数项为，这与一次函数的表示习惯不同．
方法归纳
求线性回归方程的步骤
(1)画散点图：由样本点是否呈条状分布来判断两个变量是否具有近似的线性关系．
(2)求回归系数：若存在近似的线性关系，则求回归系数．
(3)写方程：写出线性回归方程，并利用线性回归方程进行预测说明．
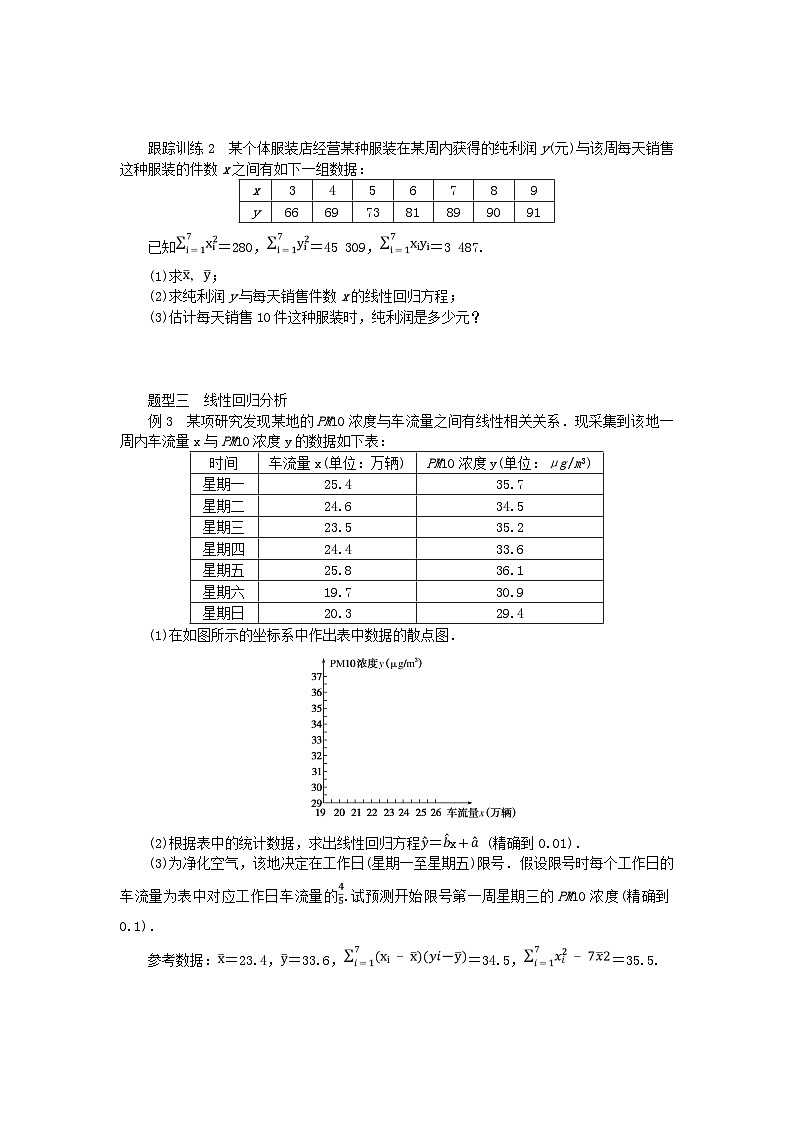
跟踪训练2 某个体服装店经营某种服装在某周内获得的纯利润y(元)与该周每天销售这种服装的件数x之间有如下一组数据：
已知＝280，＝45 309，＝3 487.
(1)求；
(2)求纯利润y与每天销售件数x的线性回归方程；
(3)估计每天销售10件这种服装时，纯利润是多少元？
题型三 线性回归分析
例3 某项研究发现某地的PM10浓度与车流量之间有线性相关关系．现采集到该地一周内车流量x与PM10浓度y的数据如下表：
(1)在如图所示的坐标系中作出表中数据的散点图．
(2)根据表中的统计数据，求出线性回归方程＝x＋ (精确到0.01)．
(3)为净化空气，该地决定在工作日(星期一至星期五)限号．假设限号时每个工作日的车流量为表中对应工作日车流量的.试预测开始限号第一周星期三的PM10浓度(精确到0.1)．
参考数据：＝23.4，＝33.6，＝34.5，＝35.5.
方法归纳
线性回归分析的注意事项
(1)求解线性回归方程时，需要进行复杂的计算，采用列表法会使计算更有条理．首先把原数据表格右边增加，xiyi，下边增加合计、平均等栏目．将需要计算的量列在表格中，再按照公式求解线性回归方程即可．如果题目给出有关数据，要注意根据数据选择求解公式．
(2)利用线性回归方程预测时要注意所得的值为估计值，不是精确值．
跟踪训练3 某公司为了预测下月产品销售情况，找出了近7个月的产品销售量y(单位：万件)的统计表：
但其中数据污损不清，经查证＝9.32，＝40.17，＝0.55.
(1)求y关于t的线性回归方程(系数精确到0.01)；
(2)公司经营期间的广告宣传费xi＝(单位：万元)(i＝1，2，…，7)，每件产品的销售价为10元，预测第8个月的毛利润能否突破15万元，请说明理由．(毛利润等于销售金额减去广告宣传费)
参考公式及数据：≈1.414，≈2.646.
易错辨析 缺失基本解题步骤致错
例4 在一次抽样检查中，抽得5个样本点，数据如下表：
试建立y关于x的回归方程．
解析：作出散点图，如图(1)所示，由散点图可以看出，图象近似反比例函数在第一象限的部分，因此
令u＝，由已知数据，可得变换后的样本数据：
作出散点图，如图(2)所示，可以看出，变换后的样本点分布在一条直线的附近，因此可以用线性回归方程拟合．
计算得＝1.55，＝7.2，＝94.25，＝21.312 5，
则＝≈4.13，＝－≈0.8.
从而得到y关于u的回归方程为＝4.13u＋0.8，则y关于x的回归方程为＝＋0.8.
【易错警示】
[课堂十分钟]
1．为了规定工时定额，需要确定加工某种零件所需的时间，为此进行了5次试验，得到5组数据：(x1，y1)，(x2，y2)，(x3，y3)，(x4，y4)，(x5，y5)，由最小二乘法求得线性回归方程为＝0.67x＋54.9.若已知x1＋x2＋x3＋x4＋x5＝150，则y1＋y2＋y3＋y4＋y5＝( )
A．75 B．155.4
C．375 D．466.2
2．某服装厂引进新技术，其生产服装的产量x(百件)与单位成本y(元)满足回归直线方程＝100.36－14.2x，则以下说法正确的是( )
A．产量每增加100件，单位成本约下降14.2元
B．产量每减少100件，单位成本约上升100.36元
C．产量每增加100件，单位成本约上升14.2元
D．产量每减少100件，单位成本约下降14.2元
3．某公司某件产品的定价x与销量y之间的数据统计表如下．根据数据，用最小二乘法得出y与x的线性回归直线方程为：y＝6.5x＋17.5，则表格中n的值应为( )
A.45 B．50
C．55 D．60
4．某设备的使用年限x与所支出的维修费用y的统计数据如下表：
根据上表可得回归直线方程为＝1.3x＋，据此模型预测，若使用年限为14年，估计维修费约为________万元．
5．某班5名学生的数学和物理成绩如下表：
(1)作出散点图；
(2)求物理成绩y对数学成绩x的线性回归方程；
(3)一名学生的数学成绩是96，试预测他的物理成绩．
§1 一元线性回归
1．1 直线拟合
1．2 一元线性回归方程
新知初探·课前预习
要点一
3．直线 直线
要点二
1．＋X
[基础自测]
1．(1)√ (2)× (3)√ (4)×
2．解析：因为＝＝1.5，＝＝4，所以样本点的中心为(1.5，4)，而直线过样本点的中心．故选D.
答案：D
3．解析：＝＝＝＝，∴回归直线过，代入验证即可．故选A.
答案：A
4．解析：线性回归方程＝x＋过样本中心点(4，5)，
所以4＋＝5；
又＋＝4，
解方程组得＝，＝，
所以线性回归方程为：＝x＋.
答案：＝x＋
题型探究·课堂解透
例1 解析：由题意，得＝＝4，＝＝5.25.∵y与x线性相关，且＝0.95x＋，∴5.25＝0.95×4＋，解得＝1.45.故选A.
答案：A
跟踪训练1 解析：在线性回归方程＝x＋中，的实际意义是x每增加一个单位，y的平均变化量，的实际意义是不受x影响的部分．∵＝－1.82，∴产量每增加1千件，单位成本约下降1.82元．故选A.
答案：A
例2 解析：(1)散点图如图所示．
(2)＝＝5，＝＝50.
∴＝＝＝6.5，
＝－＝50－6.5×5＝17.5，
所以所求的线性回归方程为＝6.5x＋17.5.
(3)根据(2)中求得的线性回归方程，当x＝10时，＝6.5×10＋17.5＝82.5，即广告费用支出为10百万元时，销售额大约为82.5百万元．
跟踪训练2 解析：(1)＝(3＋4＋5＋6＋7＋8＋9)＝6，
＝(66＋69＋73＋81＋89＋90＋91)≈79.86.
(2)设线性回归方程为＝x＋，则＝＝≈4.75
＝－＝79.86－4.75×6＝51.36.
∴所求线性回归方程为＝4.75x＋51.36.
(3)当x＝10时，y∧＝98.86，估计每天销售10件这种服装时，可获纯利润为98.86元．
例3 解析：(1)如图所示．
(2)＝＝≈0.97，＝－＝33.6－0.97×23.4≈10.90.
所以y关于x的线性回归方程为＝0.97x＋10.90.
(3)开始限号第一周星期三的车流量预计为23.5×＝18.8(万辆)，
PM10浓度预测值＝0.97×18.8＋10.90≈29.1(μg/m3)．
跟踪训练3 解析：(1)由题中和附注中的参考数据，得
＝4，＝28, ＝0.55，
＝＝40.17－4×9.32＝2.89，
又＝≈1.331，
∴＝＝≈0.103，
＝－≈1.331－0.103×4≈0.92，
所以y关于t的线性回归方程为＝0.10t＋0.92.
(2)当t＝8时，代入线性回归方程，得＝0.10×8＋0.92＝1.72(万件)，
所以第8个月的毛利润为z＝10×1.72－＝17.2－2×1.414＝14.372(万元)．
因为14.372