数学选择性必修 第二册第1章 导数及其应用1.2 导数的运算学案

这是一份数学选择性必修 第二册第1章 导数及其应用1.2 导数的运算学案，共4页。

教 材 要 点
要点一 复合函数的概念
一般地，设y＝f(u)是关于u的函数，u＝g(x)是关于x的函数，则y＝f(g(x))❶是关于x的函数，称为函数y＝f(u)和u＝g(x)的复合函数．
要点二 复合函数的求导❷法则
一般地，对于由函数y＝f(u)和u＝g(x)复合而成的函数y＝f(g(x))，它的导数与函数y＝f(u)，u＝g(x)的导数间的关系为＝____________，即y对x的导数等于________________________________________．
批注❶ 判断复合函数的复合关系的一般方法是从外向里分析，最外层的主体函数结构是以基本函数为主要结构的，内层的中间变量结构也都是基本函数关系，这样一层一层地分析．
批注❷ 关键在于：
(1)准确将复合函数分解成基本函数；
(2)正确运用复合函数的求导法则．
基 础 自 测
1．判断正误(正确的画“√”，错误的画“×”)
(1)y＝cs 3x由函数y＝cs u，u＝3x复合而成．( )
(2)函数f(x)＝sin (2x)的导数为f′(x)＝cs 2x.( )
(3)函数f(x)＝e2x－1的导数为f′(x)＝2e2x－1.( )
2．函数y＝csnx可由( )
A．y＝un和u＝csxn复合而成
B．y＝u和u＝csnx复合而成
C．y＝un和u＝csx复合而成
D．y＝cs u和u＝xn复合而成
3．函数y＝cs (－x)的导数是( )
A．cs x B．－cs x
C．－sin x D．sin x
4．已知函数f(x)＝e－x，则f′(－1)＝________．
题型探究·课堂解透——强化创新性
求复合函数的导数
例1 (1)y＝；
(2)y＝cs (x2)；
(3)y＝lg2(2x＋1)；
(4)y＝e3x＋2.
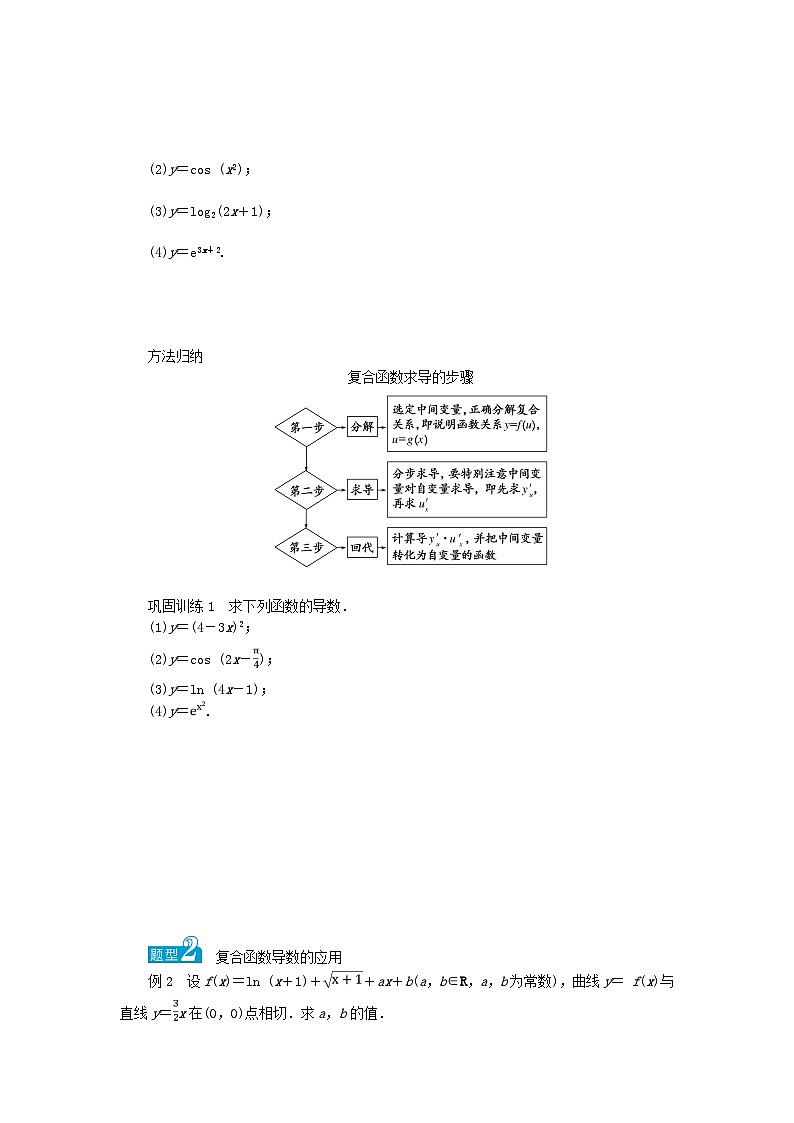
方法归纳
复合函数求导的步骤
巩固训练1 求下列函数的导数．
(1)y＝(4－3x)2；
(2)y＝cs (2x－)；
(3)y＝ln (4x－1)；
(4)y＝.
复合函数导数的应用
例2 设f(x)＝ln (x＋1)＋＋ax＋b(a，b∈R，a，b为常数)，曲线y＝ f(x)与直线y＝x在(0，0)点相切．求a，b的值．
方法归纳
解决复合函数求导与导数几何意义综合问题的方法
正确求出复合函数的导数是前提，审题时注意所给点是否是切点，挖掘题目隐含条件，求出参数，解决已知经过一定点的切线问题，寻求切点是解决问题的关键．
巩固训练2 求过点P(－1，2)且与曲线y＝3x2－4e－x＋1－2在点M(1，－3)处的切线l平行的直线方程．
1．2.3 简单复合函数的求导
新知初探·课前预习
[教材要点]
要点二
y′u·u′x y对u的导数与u对x的导数的乘积
[基础自测]
1．(1)√ (2)× (3)√
2．解析：y＝csnx，中间变量为u＝csx.
答案：C
3．解析：y′＝－sin (－x)(－x)′＝－sin x.
答案：C
4．解析：因为f′(x)＝－e－x，所以f′(－1)＝－e.
答案：－e
题型探究·课堂解透
例1 解析：(1)令u＝1－3x，则y＝＝u－4，
所以y′u＝－4u－5，u′x＝－3.
所以y′x＝y′u·u′x＝12u－5＝.
(2)令u＝x2，则y＝cs u，
所以y′x＝y′u·u′x＝－sin u·2x＝－2x sin (x2)．
(3)设y＝lg2u，u＝2x＋1，
则y′x＝y′uu′x＝＝.
(4)设y＝eu，u＝3x＋2，
则y′x＝(eu)′·(3x＋2)′＝3eu＝3e3x＋2.
巩固训练1 解析：(1)y′＝[(4－3x)2]′＝2(4－3x)·(4－3x)′
＝2(4－3x)·(－3)＝18x－24.
(2)y′＝[cs (2x－)]′＝－sin (2x－)·(2x－)′＝－2sin (2x－)．
(3)y′＝[ln (4x－1)]′＝·(4x－1)′＝.
(4)y′＝)′＝·(x2)′＝.
例2 解析：由曲线y＝f(x)过(0，0)点，
可得ln 1＋1＋b＝0，故b＝－1.
由f(x)＝ln (x＋1)＋＋ax＋b，
得f′(x)＝＋a，
则f′(0)＝1＋＋a＝＋a，
即为曲线y＝f(x)在点(0，0)处的切线的斜率．
由题意，得＋a＝，故a＝0.
巩固训练2 解析：∵y′＝(3x2－4e－x＋1－2)′＝6x＋4e－x＋1，
∴曲线在点M(1，－3)处的切线l的斜率为6＋4＝10，
过点P(－1，2)且与切线l平行的直线方程为y－2＝10(x＋1)，即10x－y＋12＝0.