高中数学湘教版（2019）选择性必修 第二册第1章 导数及其应用1.3 导数在研究函数中的应用学案

这是一份高中数学湘教版（2019）选择性必修 第二册第1章 导数及其应用1.3 导数在研究函数中的应用学案，共8页。

教 材 要 点
要点一 函数的极值与导数
批注❶ 函数极值是一个局部的概念，是仅对某一点的左右两侧附近的点而言的．
批注❷ 极值点是函数定义域上的自变量的值，而函数定义域的端点绝不是函数的极值点．
要点二 函数的驻点与极值点
(1)若f′(c)＝0，则________叫作函数f(x)的驻点．
(2)如果一个函数的导数在驻点的两侧________，则该驻点就是此函数的一个极值点❸
批注❸ 也就是说，若f′(c)存在，则f′(c)＝0是f(x)在x＝c处取到极值的必要条件，但不是充分条件．
基 础 自 测
1．判断正误(正确的画“√”，错误的画“×”)
(1)导数为0的点一定是极值点．( )
(2)函数的极大值一定大于极小值．( )
(3)函数y＝f(x)一定有极大值和极小值．( )
2．函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内有极小值点( )
A．1个 B．2个
C．3个 D．4个
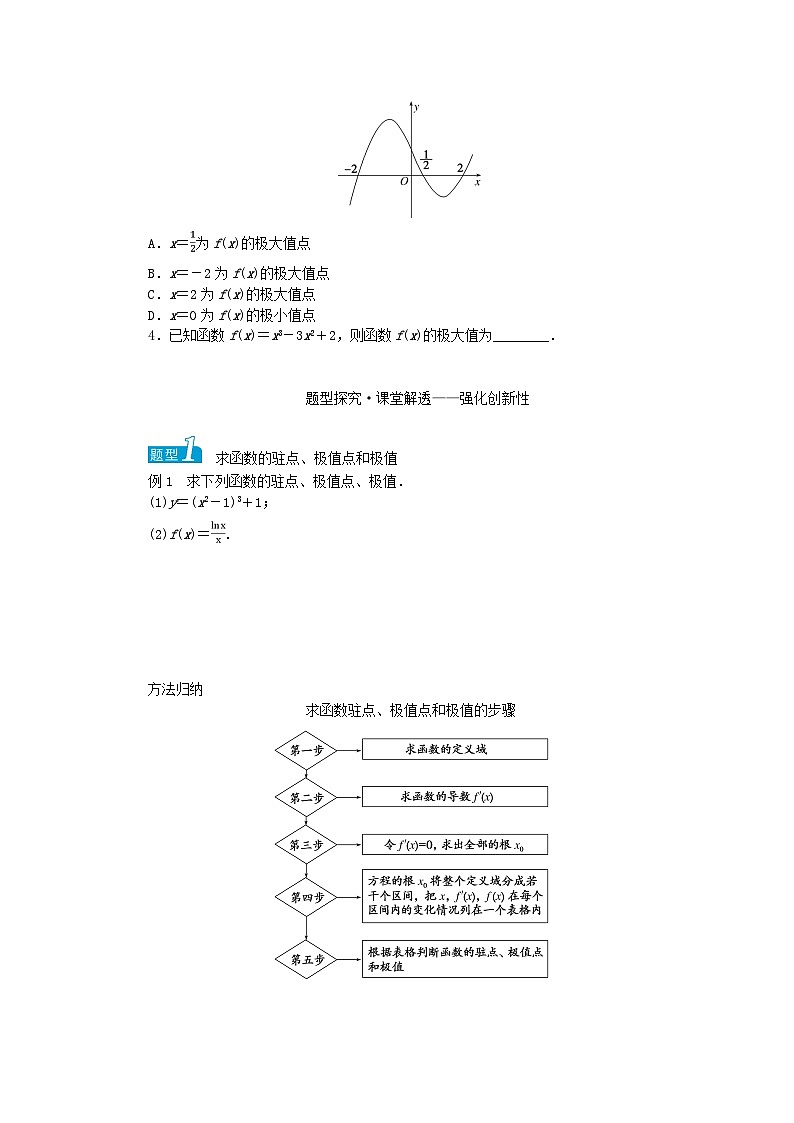
3．函数f(x)的导函数f′(x)的图象如图所示，则( )
A．x＝为f(x)的极大值点
B．x＝－2为f(x)的极大值点
C．x＝2为f(x)的极大值点
D．x＝0为f(x)的极小值点
4．已知函数f(x)＝x3－3x2＋2，则函数f(x)的极大值为________．
题型探究·课堂解透——强化创新性
求函数的驻点、极值点和极值
例1 求下列函数的驻点、极值点、极值．
(1)y＝(x2－1)3＋1；
(2)f(x)＝.
方法归纳
求函数驻点、极值点和极值的步骤
巩固训练1 求函数f(x)＝－2的驻点、极值点和极值．
已知函数极值求参数
例2 (1)若函数f(x)＝x3＋ax2＋bx＋a2在x＝1处取得极值10，则a＝________，b＝________.
(2)已知函数f(x)＝x3＋ax2－(a－1)x＋7既有极大值又有极小值，求实数a的取值范围．
已知函数极值求参数的方法
巩固训练2
(1)已知函数f(x)＝x3＋3ax2＋bx＋a2在x＝－1处有极值，则a＝________，b＝________．
(2)已知函数f(x)＝x3－(m＋3)x2＋(m＋6)x(x∈R，m为常数)，在区间(1，＋∞)内有两个极值点，求实数m的取值范围．
函数极值的综合应用
例3 若对任意a∈[3，4]，函数f(x)＝－x3＋ax2＋b(a，b∈R)在R上都有三个零点，求实数b的取值范围．
方法归纳
利用导数可以判断函数的单调性，研究函数的极值情况，并能在此基础上画出函数的大致图象，从直观上判断函数图象与x轴的交点或两个函数图象的交点的个数，从而为研究方程根的个数问题提供了方便．
巩固训练3 已知曲线f(x)＝－x3＋3x2＋9x＋a与x轴只有一个交点，求实数a的取值范围．
1．3.2 函数的极值与导数
新知初探·课前预习
[教材要点]
要点二
(1)x＝c (2)变号
[基础自测]
1．(1)× (2)× (3)×
2．解析：由导函数f′(x)在区间(a，b)内的图象可知，
函数f′(x)在(a，b)内的图象与x轴有四个公共点，
在从左到右第一个点处导数左正右负，在从左到右第二个点处导数左负右正，
在从左到右第三个点处导数左正右正，在从左到右第四个点处导数左正右负，
所以函数f(x)在开区间(a，b)内的极小值点有1个．
答案：A
3．解析：由f′(x)的图象可知，f(x)在(－∞，－2)和(，2)上单调递减，在(－2，)和(2，＋∞)上单调递增，所以x＝为f(x)的极大值点，x＝－2和x＝2为f(x)的极小值点，x＝0不是函数的极值点．
答案：A
4．解析：∵f(x)＝x3－3x2＋2，
∴f′(x)＝3x2－6x，
令f′(x)＝0，解得x1＝0，x2＝2.
所以当x＝0时，函数f(x)取得极大值，即函数f(x)的极大值为f(0)＝2.
答案：2
题型探究·课堂解透
例1 解析：(1)y′＝6x(x2－1)2＝6x(x＋1)2(x－1)2.
令y′＝0，解得x1＝－1，x2＝0，x3＝1.
当x变化时，y′，y的变化情况如下表：
∴x＝－1，x＝0，x＝1均为此函数的驻点．
x＝0是此函数的极小值点，y有极小值且极小值为0.
(2)函数f(x)＝的定义域为(0，＋∞)，
且f′(x)＝.
令f′(x)＝0，解得x＝e.
当x变化时，f′(x)与f(x)的变化情况如下表：
因此，x＝e是函数的驻点也是极大值点，极大值为f(e)＝，没有极小值．
巩固训练1 解析：函数f(x)的定义域为R.
f′(x)＝＝－.
令f′(x)＝0，得x＝－1或x＝1.
当x变化时，f′(x)，f(x)的变化情况如下表：
由上表可以看出，x＝－1和x＝1是函数的驻点．
x＝－1是函数的极小值点，且极小值为f(－1)＝－3；
x＝1是函数的极大值点，且极大值为f(1)＝－1.
例2 解析：(1)f′(x)＝3x2＋2ax＋b，
依题意得即
解得或
但由于当a＝－3，b＝3时，f′(x)＝3x2－6x＋3＝3(x－1)2≥0，故f(x)在R上单调递增，不可能在x＝1处取得极值，所以不符合题意，应舍去．而当时，经检验知符合题意，故a，b的值分别为4，－11.
(2)f′(x)＝3x2＋2ax－a＋1.函数f(x)＝x3＋ax2－(a－1)x＋7既有极大值又有极小值，由二次函数图象可知，只需函数f′(x)有两个零点，即f′(x)＝0有两个不同的实数解，
则Δ＝4a2＋12(a－1)>0，
解得a<或a>.
所以实数a的取值范围是(－∞，，＋∞)．
答案：(1)4 －11 (2)见解析
巩固训练2 解析：(1)∵f′(x)＝3x2＋6ax＋b，且函数f(x)在x＝－1处有极值0，
∴即
解得或
当a＝1，b＝3时，f′(x)＝3x2＋6x＋3＝3(x＋1)2≥0，此时函数f(x)在R上为增函数，无极值，故舍去．
当a＝2，b＝9时，
f′(x)＝3x2＋12x＋9＝3(x＋1)(x＋3)．
当x∈(－∞，－3)时，f′(x)>0，此时f(x)为增函数；
当x∈(－3，－1)时，f′(x)<0，此时f(x)为减函数；
当x∈(－1，＋∞)时，f′(x)>0，此时f(x)为增函数．
故f(x)在x＝－1时取得极小值，
∴a＝2，b＝9.
(2)f′(x)＝x2－(m＋3)x＋m＋6.
因为函数f(x)在区间(1，＋∞)内有两个极值点，
所以f′(x)＝x2－(m＋3)x＋m＋6在(1，＋∞)内与x轴有两个不同的交点，如图所示．
所以
解得m>3.故实数m的取值范围是(3，＋∞)．
答案：(1)2 9 (2)见解析
例3 解析：因为f(x)＝－x3＋ax2＋b，
所以f′(x)＝－3x2＋2ax＝－3x(x－)．a∈[3，4]，
令f′(x)>0，即－3x(x－)>0，解得0所以f(x)极大值＝f＝＋b，
f(x)极小值＝f(0)＝b.
由于对任意a∈[3，4]，
函数f(x)在R上都有三个零点，
所以即
解得－因为对任意a∈[3，4]，b>－恒成立，
所以b>(－)max＝－＝－4.
所以实数b的取值范围为(－4，0)．
巩固训练3 解析：f′(x)＝－3x2＋6x＋9.
令f′(x)＝0，解得x1＝－1，x2＝3.
列表：
所以当x＝－1时，f(x)有极小值f(－1)＝a－5；
当x＝3时，f(x)有极大值f(3)＝a＋27.
画出大致图象，要使f(x)的图象与x轴只有一个交点，只需极大值小于0(如图1)或极小值大于0(如图2)．
所以a＋27<0或a－5>0，解得a<－27或a>5.
故实数a的取值范围为a<－27或a>5.
条件
f′(x0)
x0附近的左侧f′(x)≥0，右侧f′(x)≤0
x0附近的左侧f′(x)≤0，右侧f′(x)≥0
图象
极值❶
f(x0)为极大值
f(x0)为极小值
极值点❷
x0为极大值点
x0为极小值点
x
(－∞，0)
0
(0，2)
2
(2，＋∞)
f′(x)
＋
0
－
0
＋
f(x)
↗
极大值
↘
极小值
↗
x
(－∞，－1)
－1
(－1，0)
0
(0，1)
1
(1，＋∞)
y′
－
0
－
0
＋
0
＋
y
↘
无极值
↘
极小值0
↗
无极值
↗
x
(0，e)
e
(e，＋∞)
f′(x)
＋
0
－
f(x)
↗
↘
x
(－∞，－1)
－1
(－1，1)
1
(1，＋∞)
f′(x)
－
0
＋
0
－
f(x)
↘
极小值
↗
极大值
↘
x
(－∞，－1)
－1
(－1，3)
3
(3，＋∞)
f′(x)
－
0
＋
0
－
f(x)
↘
极小值
↗
极大值
↘