
- 新教材2023版高中数学第2章空间向量与立体几何2.1空间直角坐标系2.1.1建立空间直角坐标系学案湘教版选择性必修第二册 学案 0 次下载
- 新教材2023版高中数学第2章空间向量与立体几何2.1空间直角坐标系2.1.2空间两点间的距离学案湘教版选择性必修第二册 学案 0 次下载
- 新教材2023版高中数学第2章空间向量与立体几何2.3空间向量基本定理及坐标表示2.3.1空间向量的分解与坐标表示学案湘教版选择性必修第二册 学案 0 次下载
- 新教材2023版高中数学第2章空间向量与立体几何2.3空间向量基本定理及坐标表示2.3.2空间向量运算的坐标表示学案湘教版选择性必修第二册 学案 0 次下载
- 新教材2023版高中数学第2章空间向量与立体几何2.4空间向量在立体几何中的应用2.4.1空间直线的方向向量和平面的法向量学案湘教版选择性必修第二册 学案 0 次下载
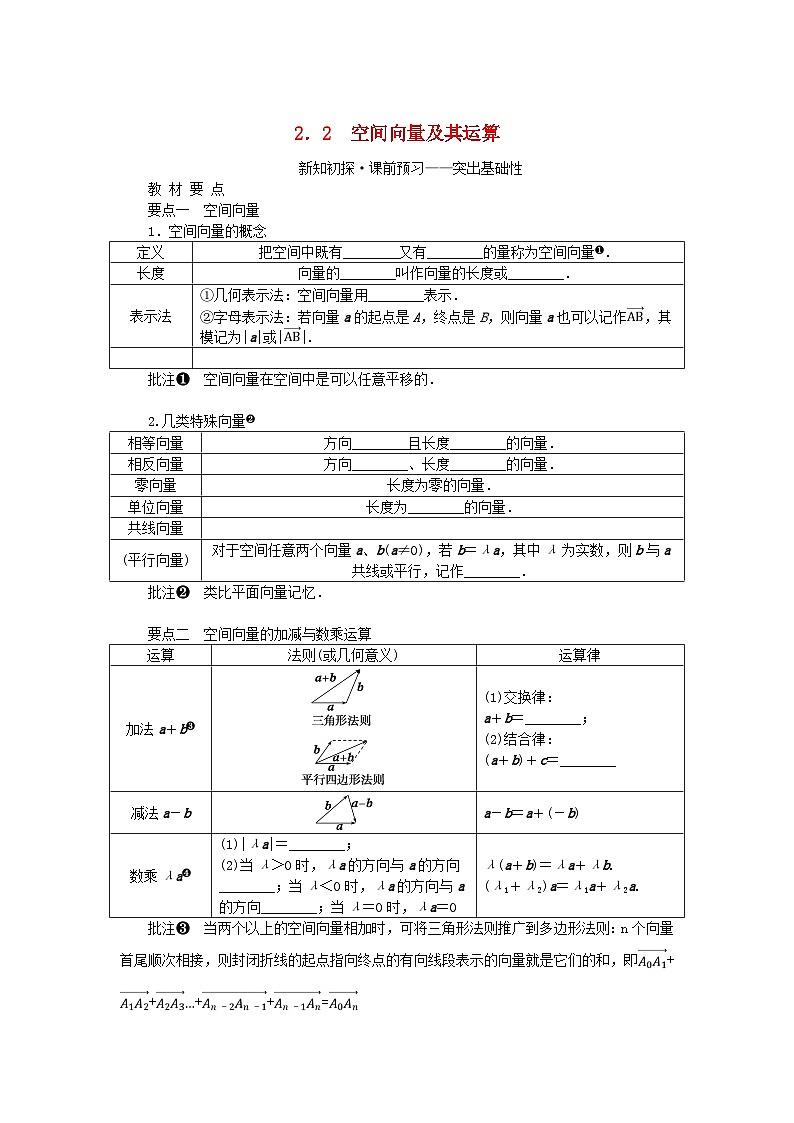
湘教版(2019)选择性必修 第二册2.2 空间向量及其运算学案
展开教 材 要 点
要点一 空间向量
1.空间向量的概念
批注❶ 空间向量在空间中是可以任意平移的.
2.几类特殊向量❷
批注❷ 类比平面向量记忆.
要点二 空间向量的加减与数乘运算
批注❸ 当两个以上的空间向量相加时,可将三角形法则推广到多边形法则:n个向量首尾顺次相接,则封闭折线的起点指向终点的有向线段表示的向量就是它们的和,即++++=
批注❹ 注意实数与向量的乘积的特殊情况:当λ=0时,λ=;当λ≠0时,若=,则λ=.
要点三 空间向量的数量积
1.空间向量的夹角
已知两个非零向量a,b,在空间任取一点O,作=a,=b,则∠AOB叫做向量a,b的夹角❺,记作________,其取值范围为[0,π].
批注❺ 关键是起点相同!
2.空间向量的数量积
定义a·b=|a||b|cs 〈a,b〉❻为a与b的数量积.
批注❻
(1)两个向量的数量积是数量,而不是向量.
(2)零向量与任意向量的数量积等于零.
3.性质
a·b=0⇔________,a·a=________,|a|=________,cs 〈a,b〉=________.
4.运算律❼
λ(a·b)=________,a·b=________(交换律),a·(b+c)=________(分配律).
批注❼ 特别提醒:不满足结合律(·)·=·(·).
5.投影向量
如图,将空间任意两个向量a,b平移到同一个平面内,可得=a,=b,〈a,b〉=α.过点B作BB1⊥OA,垂足为点B1,则________为在方向上的投影向量,投影向量的模________=|||cs α|称为投影长,称________为在方向上的投影,其正负表示与方向相同还是相反.
基 础 自 测
1.判断正误(正确的画“√”,错误的画“×”)
(1)空间两个向量的加减运算与平面内两向量的加减法运算完全一致.( )
(2)对于任意向量a,b,c,都有(a·b)c=a(b·c).( )
(3)若a·b=b·c,且b≠0,则a=c.( )
2.下列说法正确的是( )
A.任一空间向量与它的相反向量都不相等
B.将空间向量所有的单位向量平移到同一起点,则它们的终点构成一个圆
C.模长为3的空间向量大于模长为1的空间向量
D.不相等的两个空间向量的模可能相等
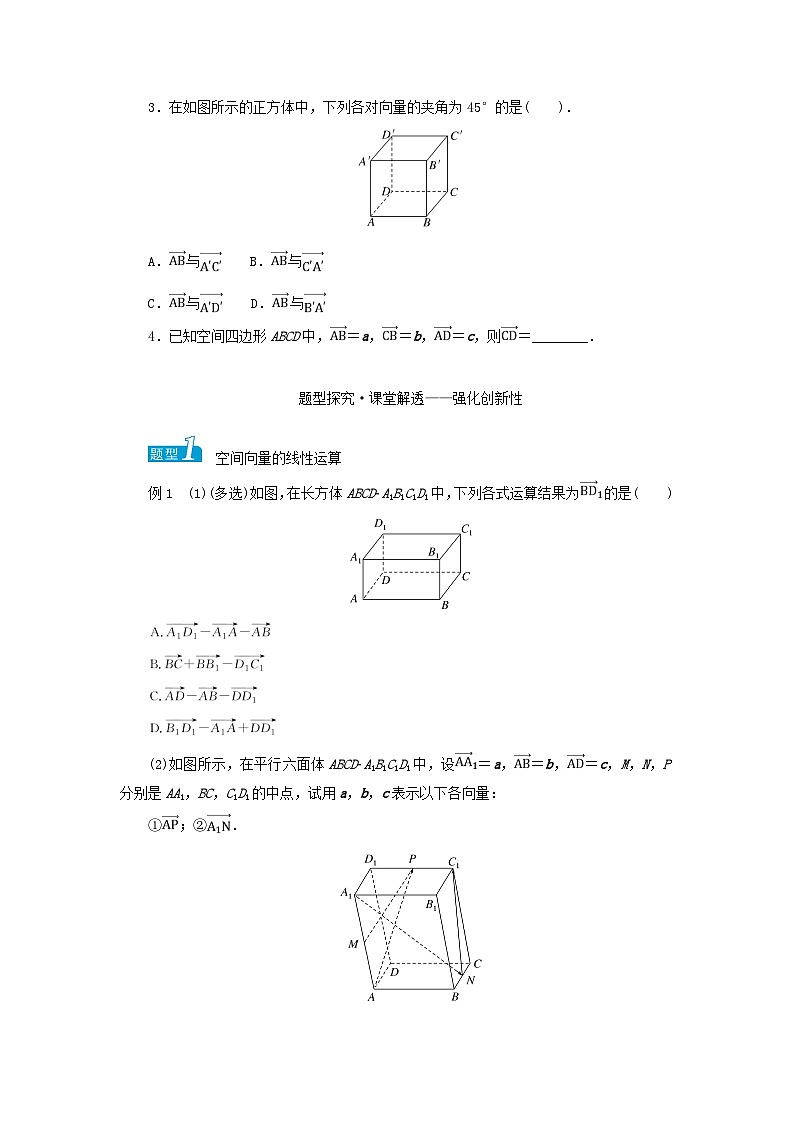
3.在如图所示的正方体中,下列各对向量的夹角为45°的是( ).
A.与 B.与
C.与 D.与
4.已知空间四边形ABCD中,=a,=b,=c,则=________.
题型探究·课堂解透——强化创新性
空间向量的线性运算
例1 (1)(多选)如图,在长方体ABCDA1B1C1D1中,下列各式运算结果为的是( )
(2)如图所示,在平行六面体ABCDA1B1C1D1中,设=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
①;②.
方法归纳
空间向量线性运算的3个技巧
巩固训练1
如图所示,在平行六面体中,O为AC的中点.
(1)化简:-;
(2)设E是棱DD1上的点,且=,若=,试求实数x,y,z的值.
共线向量的应用
例2 如图,在正方体ABCDA1B1C1D1中,E在A1D1上,且=,F在对角线上,且A1F=,求证:E,F,B三点共线.
方法归纳
证明空间三点共线的三种思路
巩固训练2 如图所示,已知空间四边形ABCD,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且==.求证:四边形EFGH是梯形.
空间向量数量积的运算
例3 如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求:
(1)·;(2)·;
(3)·;(4)·.
方法归纳
计算空间向量数量积的2种方法
巩固训练3 如图,正方体ABCDA1B1C1D1的边长为1,求:
;
;
.
空间向量数量积的应用
例4 已知平行六面体ABCDA′B′C′D′的各棱长均为1,且∠A′AB=∠A′AD=∠BAD=.
(1)求证:AA′⊥BD;
(2)求对角线AC′的长.
方法归纳
利用向量数量积判断或证明垂直问题的策略
巩固训练4 如图,正方体ABCD-A1B1C1D1中,E,F,G分别是棱CC1,BC,CD的中点,求证:A1G⊥平面DEF.
2.2 空间向量及其运算
新知初探·课前预习
[教材要点]
要点一
1.大小 方向 大小 模 有向线段
2.相同 相等 相反 相等 1 b∥a
要点二
b+a a+(b+c) |λ||a| 相同 相反
要点三
1.〈a,b〉
3.a⊥b |a|2
4.(λa)·b b·a a·b+a·c
5. || ||cs α
[基础自测]
1.(1)√ (2)× (3)×
2.解析:对A,零向量的相反向量是本身,故A错;
对B,终点构成一个球面,故B错;
对C,向量不能比较大小,故C错;
对D,相反向量是不相等向量,但它们的模长相等,故D正确.
答案:D
3.解析:对于A,因为=,所以与的夹角为45°,故A正确;
对于B,因为=,所以与的夹角为135°,故B不正确;
对于C,因为=,所以与的夹角为90°,故C不正确;
对于D,因为=,所以与的夹角为180°,故D不正确.
答案:A
4.解析:===-a+b+c.
答案:-a+b+c
题型探究·课堂解透
例1 解析:(1)A中--=-=;
B中==;
C中===;
D中==.
(2)①∵点P是C1D1的中点,
∴=+=+=a+c+b.
②∵点N是BC的中点,
∴=+=+=-a+b+c.
答案:(1)AB (2)见解析
巩固训练1 解析:(1)-)=-=-+=.
(2)===,
∴x=、y=-、z=-.
例2 证明:设=a,==c.
∵=,=,
∴=,=.
∴==b,=)=)=a+b-c.
∴=-=a-b-c=(a-b-c).
又=++=-b-c+a=a-b-c,
∴=,所以E,F,B三点共线.
巩固训练2 证明:∵E,H分别是边AB,AD的中点,
∴==.
则===)=.
∵===)=,
∴∥且||=||≠||.
又F不在EH上,故四边形EFGH是梯形.
例3 解析:(1)·=·=||||·cs 〈,〉=cs 60°=.
(2)·=·=||2=.
(3)·=·=||·||cs 〈〉=cs 120°=-.
(4)·=·()=··=||||cs 〈〉-||||cs 〈〉=cs 60°-cs 60°=0.
巩固训练3 解析:=0.
=|cs 45°=1.
=〉
==-1.
例4 解析:
(1)证明:由题意,平行六面体ABCD A′B′C′D′的各棱长均为1,∠A′AB=∠A′AD=∠BAD=,
因为=,
所以·=·()=··=||·||cs ∠A′AD-||·||cs ∠A′AB=1×1×-1×1×=0,
所以AA′⊥BD.
(2)因为===,
所以||2=()2=+2(···)
=12+12+12+2(1×1×+1×1×+1×1×)=6.
所以||=.
巩固训练4 证明:设正方体的棱长为a,
∵·=(+)·()
=···+···
=··=a2-a2=0,
∴A1G⊥DF.
同理可证A1G⊥DE,又DF=D,
∴A1G⊥平面DEF.定义
把空间中既有________又有________的量称为空间向量❶.
长度
向量的________叫作向量的长度或________.
表示法
①几何表示法:空间向量用________表示.
②字母表示法:若向量a的起点是A,终点是B,则向量a也可以记作,其模记为|a|或||.
相等向量
方向________且长度________的向量.
相反向量
方向________、长度________的向量.
零向量
长度为零的向量.
单位向量
长度为________的向量.
共线向量
(平行向量)
对于空间任意两个向量a、b(a≠0),若b=λa,其中λ为实数,则b与a共线或平行,记作________.
运算
法则(或几何意义)
运算律
加法a+b❸
(1)交换律:
a+b=________;
(2)结合律:
(a+b)+c=________
减法a-b
a-b=a+(-b)
数乘λa❹
(1)|λa|=________;
(2)当λ>0时,λa的方向与a的方向________;当λ<0时,λa的方向与a的方向________;当λ=0时,λa=0
λ(a+b)=λa+λb.
(λ1+λ2)a=λ1a+λ2a.
高中数学湘教版(2019)选择性必修 第二册3.3 正态分布导学案: 这是一份高中数学湘教版(2019)选择性必修 第二册3.3 正态分布导学案,共6页。
高中数学湘教版(2019)选择性必修 第二册2.4 空间向量在立体几何中的应用第1课时学案: 这是一份高中数学湘教版(2019)选择性必修 第二册2.4 空间向量在立体几何中的应用第1课时学案,共9页。
湘教版(2019)选择性必修 第二册2.3 空间向量基本定理及坐标表示学案及答案: 这是一份湘教版(2019)选择性必修 第二册2.3 空间向量基本定理及坐标表示学案及答案,共7页。













