2023-2024学年天津市滨海新区八年级（上）期末数学练习试卷（含解析）

这是一份2023-2024学年天津市滨海新区八年级（上）期末数学练习试卷（含解析），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是( )
A. B. C. D.
2.下列长度的三条线段，能构成三角形的是( )
A. 3，10，5B. 4，8，4C. 5，13，12D. 2，7，4
3.一个数是0.0000003，这个数用科学记数法表示为( )
A. 3×10−5B. 3×10−6C. 3×10−7D. 3×10−8
4.已知x+y=6，xy=5，则(x−y)2的值为( )
A. 25B. 36C. 11D. 16
5.化简x(x−1)2−1(x−1)2的结果为( )
A. x(x−1)2B. 1x−1C. 1(x−1)2D. 1
6.如图，△ABC≌△DEF，AD=2.2，CF=4.4，则AC的长度等于( )
A. 2.2
B. 1.1
C. 3.3
D. 2.3
7.计算(−12a)(2a2−23a+56)的结果是( )
A. −24a3+8a2B. −24a3−8a2−10a
C. −24a3+8a2−10aD. −24a2+8a+10
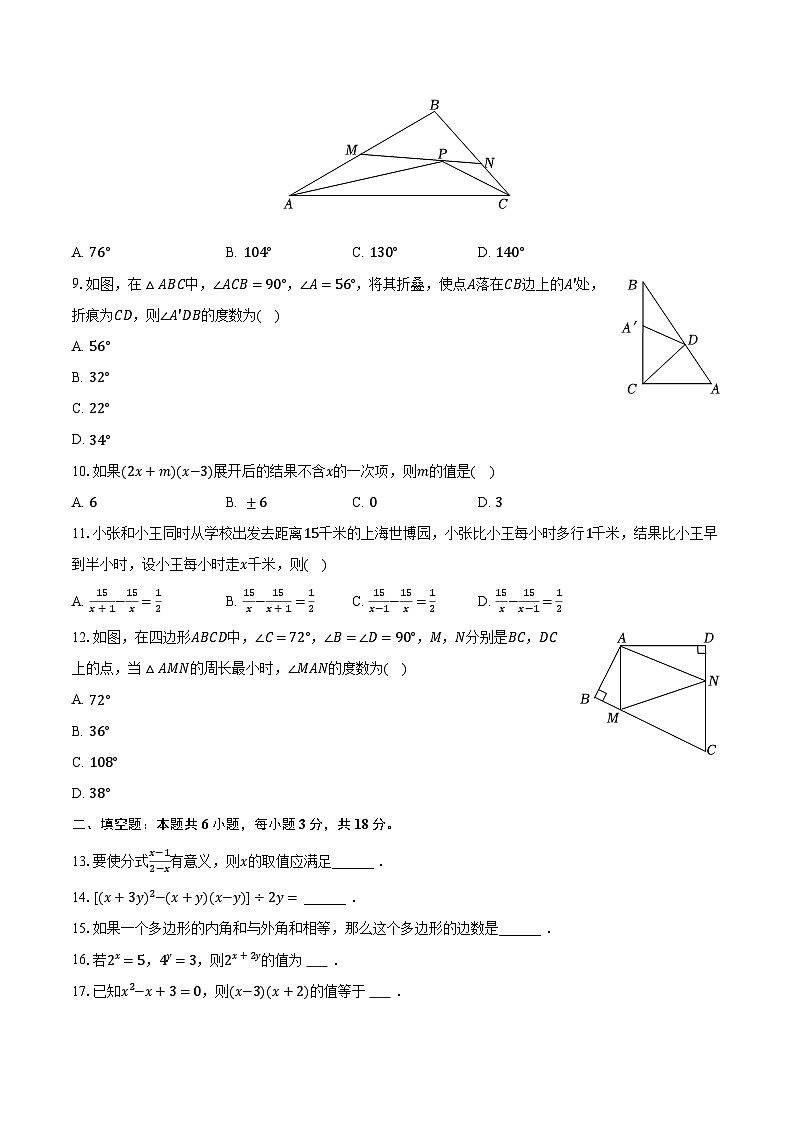
8.如图，点P为△ABC内一点，过点P的线段MN分别交AB，BC于点M，N，且M，N分别在PA，PC的垂直平分线上.若∠APC=142°，则∠ABC的度数为( )
A. 76°B. 104°C. 130°D. 140°
9.如图，在△ABC中，∠ACB=90°，∠A=56°，将其折叠，使点A落在CB边上的A′处，折痕为CD，则∠A′DB的度数为( )
A. 56°
B. 32°
C. 22°
D. 34°
10.如果(2x+m)(x−3)展开后的结果不含x的一次项，则m的值是( )
A. 6B. ±6C. 0D. 3
11.小张和小王同时从学校出发去距离15千米的上海世博园，小张比小王每小时多行1千米，结果比小王早到半小时，设小王每小时走x千米，则( )
A. 15x+1−15x=12B. 15x−15x+1=12C. 15x−1−15x=12D. 15x−15x−1=12
12.如图，在四边形ABCD中，∠C=72°，∠B=∠D=90°，M，N分别是BC，DC上的点，当△AMN的周长最小时，∠MAN的度数为( )
A. 72°
B. 36°
C. 108°
D. 38°
二、填空题：本题共6小题，每小题3分，共18分。
13.要使分式x−12−x有意义，则x的取值应满足______ ．
14.[(x+3y)2−(x+y)(x−y)]÷2y= ______ ．
15.如果一个多边形的内角和与外角和相等，那么这个多边形的边数是______ ．
16.若2x=5，4y=3，则2x+2y的值为 ．
17.已知x2−x+3=0，则(x−3)(x+2)的值等于 ．
18.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=9，BD是△ABC的角平分线，点P，点N分别是BD，AC边上的动点，点M在BC上，且BM=2．
(Ⅰ)PM+PN是否存在最小值？ (填“是”或“否”)．
(Ⅱ)如果存在，请直接写出此时PM+PN的最小值；如果不存在，请说明理由．
．
三、解答题：本题共7小题，共56分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
计算：
(Ⅰ)(a2b3)−1⋅(ab−2)2；
(Ⅱ)x2⋅x4−(2x3)2+x7÷x．
20.(本小题8分)
先化简.再求值：(a+7a−1−2a+1)÷a2+3aa2−1，其中a=−2．
21.(本小题8分)
如图，AD是△ABC边BC上的高，BE平分∠ABC交AD于点E，若∠C=65°，∠BED=68°，求∠ABC和∠BAC的度数．
22.(本小题8分)
因式分解：
(Ⅰ)mx2−2m2x+m3；
(Ⅱ)8m2n+2mn．
23.(本小题8分)
中华优秀传统文化是中华民族的“根”和“魂”，是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化，某校为各班购进《三国演义》和《水浒传》连环画若干套，其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元.已知该校购买《三国演义》和《水浒传》连环画的费用分别为3600元和4800元，购买《三国演义》连环画的套数是购买《水浒传》连环画套数的一半，求每套《水浒传》连环画的价格．
(1)设每套《水浒传》连环画的价格为x元，用含x的式子表示：
每套《三国演义》连环画的价格为______ 元，购买《三国演义》连环画的套数是______ ，购买《水浒传》连环画套数是______ ．
(2)列出方程，完成本题解答．
24.(本小题8分)
如图，在△ABC中，∠ACB=90°，CA=CB，点D在BC上，点E是AC延长线上一点，且BE=AD．
(1)求证：△ACD≌△BCE；
(2)若∠BAD=22°，求∠ABE的度数．
25.(本小题8分)
如图，等边△ABC的边长为3，点D是AB延长线上的一个动点，以CD为边在AD上方作等边△CDM，过点A作AN⊥AD，连接MB并延长，交AN于点N．
(Ⅰ)求证：MB=DA；
(Ⅱ)当∠DCA=100°时，求∠DMN的度数；
(Ⅲ)在点D的运动过程中，线段BN的长度是否会发生变化？若不变，则求出BN的长度；若变化，请说明理由．
答案和解析
1.【答案】A
【解析】解：选项B、C、D不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
选项A能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：A．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】C
【解析】解：A、3+513，能够组成三角形，符合题意；
D、2+4