

2023-2024学年山东省烟台市招远重点中学高一(上)期末数学模拟试卷(含解析)
展开1.已知集合A={x|y=lg2(2−x)},B={y|y=2x−1,x∈R},则A∩B=( )
A. (−1,2)B. (−∞,2)C. (0,2)D. (−1,+∞)
2.函数y=−e−x与y=ex的图象( )
A. 关于x轴对称B. 关于y轴对称
C. 关于原点对称D. 关于直线y=x对称
3.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=e−x−2,则f(ln12)=( )
A. −32B. 32C. 0D. 2
4.下列函数为奇函数的是( )
A. y=|sinx|B. y=1−cs2xC. y=−3sin2xD. y=1+tanx
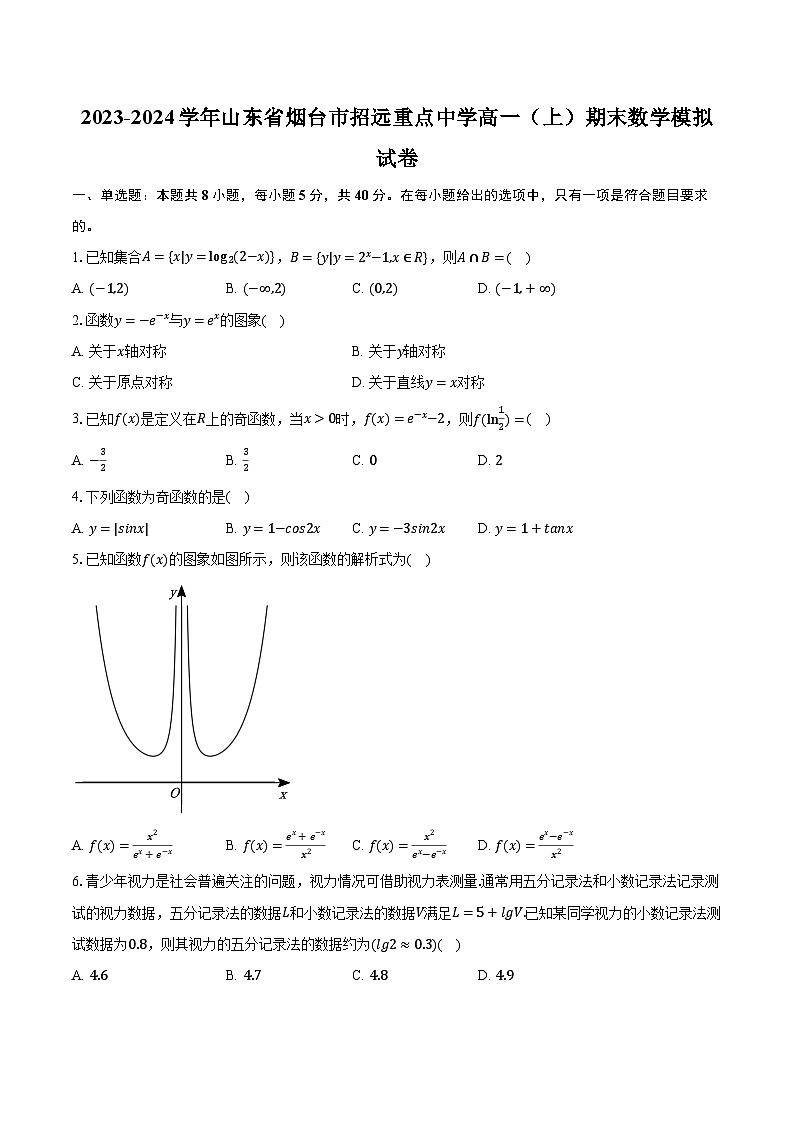
5.已知函数f(x)的图象如图所示,则该函数的解析式为( )
A. f(x)=x2ex+e−xB. f(x)=ex+e−xx2C. f(x)=x2ex−e−xD. f(x)=ex−e−xx2
6.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录测试的视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lgV.已知某同学视力的小数记录法测试数据为0.8,则其视力的五分记录法的数据约为(lg2≈0.3)( )
A. 4.6B. 4.7C. 4.8D. 4.9
7.如图,直线AB与单位圆相切于点O,射线OP从OA出发绕着点O逆时针旋转,在此过程中,记∠AOP=x(0
B. ∃x1≠x2,使得f(x1)=f(x2)
C. 对∀x∈(0,π2),都有f(π2+x)=f(x)+π2
D. 对∀x∈(0,π2),都有f(π2−x)+f(π2+x)=π
8.已知函数f(x)=ex+x−2的零点为m,g(x)=lnx+x−2的零点为n,则下列不等式成立的是( )
A. mn>1B. m2+n2<3C. 4m2>n2D. em+lnn<2
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的有( )
A. θ为第三象限角的充要条件为sinθtanθ<0
B. 若θ为第二象限角,则θ2为第一或第三象限角
C. 1−sin(θ−2π)sin(π+θ)−2cs2(π2−θ)=cs2θ
D. sin(−1071°)sin99°+sin(−171°)sin(−261°)=0
10.关于函数f(x)=4x−14x+1−a⋅2x,下列结论中正确的是( )
A. 当a=0时,f(x)是增函数B. 当a=0时,f(x)的值域为(−1,+∞)
C. 当a=1时,f(x)是奇函数D. 若f(x)的定义域为R,则a<2
11.高斯是德国著名的数学家,近代数学奠基者之一,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,例如:[−π]=−4,[1.5]=1,已知函数f(x)=2x−11+2x,设g(x)=[f(x)],则( )
A. f(x)是奇函数B. g(x)是奇函数
C. f(x)在R上是增函数D. g(x)的值域是{−1,0}
12.已知函数f(x)=ax+1,x≤0−|lnx|,x>0,若g(x)=f(f(x))+1,则( )
A. 当a>0时,g(x)有4个零点B. 当a>0时,g(x)有5个零点
C. 当a<0时,g(x)有1个零点D. 当a<0时,g(x)有2个零点
三、填空题:本题共4小题,每小题5分,共20分。
13.函数f(x)= 1−lnx的定义域为______.
14.若圆心角为4π3的扇形的面积为6π,则该扇形的半径为______ .
15.已知0.3a=2,则lg2.42= ______ .(结果用含a的式子表示)
16.已知函数f(x)=x2+2x−3,x≤0−2+lnx,x>0,当方程f(x)=k有3个实数解时,k的取值范围是______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题10分)
计算下列各式的值:
(1) (π−134)2+(1649)−12+(−8)23+80.25×42+3(π−2)3;
(2)12lg25+lg2−lg 0.1−lg29×lg32.
18.(本小题12分)
已知tanα=2,π<α<3π2.
(1)求sin2α−2cs2α的值;
(2)sinα−csα的值.
19.(本小题12分)
已知函数f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=2x+1.
(1)求函数f(x),g(x)的解析式;
(2)若对任意x∈[1,+∞),不等式f(2x)≥mg(x)−2恒成立,求实数m的最大值.
20.(本小题12分)
某工厂生产的废气经过滤后排放,过滤过程中废气的污染物含量P(单位:mg/L)与时间t(单位:h)间的关系为P=P0e−kt,其中P0,k为正常数,已知在前5h消除了10%的污染物.
(1)10h后还剩百分之几的污染物?
(2)要使污染物减少三分之一以上至少需要多少时间?(结果精确到1h)
(参考数据ln2=0.69,ln3=1.1,ln5=1.61)
21.(本小题12分)
已知f(x)是定义在R的偶函数,且f(x)=lg3(3x+1)−kx,g(x)=f(x)+12x.
(1)求f(x)的解析式;
(2)设h(x)=x2−2tx+5,若存在x1∈[lg32,8],对任意的x2∈[1,4],都有g(x1)≤h(x2),求实数t的取值范围.
22.(本小题12分)
已知函数f(x)=lgλx+1x.
(1)当λ=2时,解不等式f(x)>0;
(2)设λ>0,当a∈[12,2]时,对任意x1,x2∈[a,a+1],都有|f(x1)−f(x2)|≤lg2,求λ的取值范围.
答案和解析
1.【答案】A
【解析】解:A={x|y=lg2(2−x)},因为2−x>0,所以A={x|x<2},
B={y|y=2x−1,x∈R},因为2x>0,所以B={y|y>−1},
所以A∩B={x|−1
计算集合A中函数的定义域,和集合B中函数的值域,再求两个集合的交集.
本题考查了对数函数的定义域,指数函数的值域,交集的运算,是基础题.
2.【答案】C
【解析】解:根据题意,y=−e−x相当于y=ex的图象先沿y轴对称翻折,再沿着x轴对称翻折,
故翻折后的图象与原图象关于原点对称.
故选:C.
根据题意,根据函数图象的变换即可得到答案.
本题考查函数的图象分析,涉及函数的对称变换,属于基础题.
3.【答案】B
【解析】解:根据题意得ln12=−ln2,ln2>0,−ln2<0,
又因为f(x)是定义在R上的奇函数,当x>0时,f(x)=e−x−2,
所以f(ln12)=f(−ln2)=−f(ln2)=−(e−ln2−2)=−(12−2)=32.
故选:B.
利用函数的解析式以及函数的奇偶性的性质求解函数值即可.
本题考查函数的奇偶性的性质与应用,属于基础题.
4.【答案】C
【解析】解:根据题意,依次分析选项:
对于A,由y=f(x)=|sinx|,定义域为R,关于原点对称,则f(−x)=|sin(−x)|=|sinx|=f(x),所以f(x)是偶函数,故A错误;
对于B,由y=f(x)=1−cs2x,定义域为R,关于原点对称,则f(−x)=1−cs(−2x)=1−cs2x=f(x),所以f(x)是偶函数,故B错误;
对于C,由y=f(x)=−3sin2x,定义域为R,关于原点对称,则f(−x)=−3sin(−2x)=3sin2x=−f(x),所以f(x)是奇函数,故C正确;
对于D,由y=f(x)=1+tanx,定义域为{x|x≠kπ+π2,k∈Z},关于原点对称,则f(−x)=1+tan(−x)=1−tanx≠f(x),且f(−x)≠−f(x),所以f(x)非奇非偶,故D错误.
故选:C.
根据题意,依次分析选项中函数的奇偶性,综合可得答案.
本题考查函数奇偶性的判断,注意函数奇偶性的定义,属于基础题.
5.【答案】B
【解析】解:根据函数的图象,函数的图象关于y轴对称,
故该函数为偶函数,而选项C和D的关系式符合奇函数的图象,故选项C和D排除,
对于选项A:函数f(x)的关系式符合偶函数,但是当x→+∞时,f(x)→+0,故排除选项A;
对于选项B:当x→+∞时,函数f(x)→+∞,当x→0时,函数f(x)→+∞,当x=x0时,f(x)取得最小值,由于函数的关系式符合偶函数,故选项B符合.
故选:B.
直接利用函数的奇偶性和函数的单调性的应用判断A、B、C、D的结果.
本题考查的知识要点:函数的关系式,函数的奇偶性的判定和函数的单调性的判定,主要考查学生的运算能力和数学思维能力,属于基础题.
6.【答案】D
【解析】解:由题意L=5+lgV,当V=0.8时,
则L=5+lg0.8=5+lg810=5+3lg2−1≈4+3×0.3=4.9.
故选:D.
由L,V的关系,代入V=0.8,利用对数运算性质化简求值即可.
本题考查对数运算的应用,属于基础题.
7.【答案】D
【解析】解:如下图(OD与OP重合),设∠OCD=2x,则阴影部分面积f(x)=12×1×2x−12sin2x=x−12sin2x,且0
由图知在旋转过程中阴影面积不断变大,不存在x1≠x2使得f(x1)=f(x2),所以B错;
当x∈(0,π2),则f(π2+x)=π2+x−12sin(π+2x)=π2+x+12sin2x≠π2+f(x),所以C错;
f(π2−x)+f(π2+x)=π2−x+π2+x−12sin(π−2x)−12sin(π+2x)=π−sin2x+sin2x=π,所以D对.
故选:D.
根据题设可得f(x)=x−12sin2x,且0
8.【答案】B
【解析】解:由f(x)=0,g(x)=0得ex=2−x,lnx=2−x,即可得em=2−m,lnn=2−n,
即有em+lnn=4−(m+n),函数y=ex与y=lnx互为反函数,
在同一坐标系中分别作出函数y=ex,y=lnx,y=2−x的图象,如图所示,
则A(m,em),B(n,lnn),由反函数性质知,A,B关于(1,1)对称,
则m+n=2,em+lnn=2,mn<(m+n)24=1,A、D错误,
∵f(x)在R上为增函数,f(0)=−1<0,f(12)= e−32>0,∴0
∵0
把问题转化为两个函数图象交点问题,根据反函数的性质、基本不等式、进行逐一判断即可.
本题考查函数的零点与方程根的关系,函数零点转化为两个函数交点的形式利用数形结合思想进行求解是解题的关键,是中档题.
9.【答案】BCD
【解析】解:对于A,当θ为第三象限角时,sinθ<0,tanθ>0,所以sinθtanθ<0,
反之,当sinθtanθ<0时,则有
①当sinθ<0,tanθ>0,θ为第三象限角,
②当sinθ>0,tanθ<0时,θ为第二象限角,故A错误;
对于B,若θ为第二象限角,即π2+2kπ<θ<π+2kπ,k∈Z,
则π4+kπ<θ<π2+kπ,k∈Z,则θ2为第一或第三象限角,故B正确;
对于C,1−sin(θ−2π)sin(π+θ)−2cs2(π2−θ)=1+sin2θ−2sin2θ=1−sin2θ=cs2θ,故C正确;
对于D,sin(−1071°)sin99°+sin(−171°)sin(−261°)=−sin1071°sin99°+sin171°sin261°
=−sin(1080°−9°)sin(90°+9°)+sin(180°−9°)sin(180°+81°)
=sin9°cs9°−sin9°sin81°
=sin9°cs9°−sin9°cs9°=0,故D正确.
故选:BCD.
利用三角函数角在各象限三角函数值的正负,以及角在各象限范围,诱导公式,同角三角函数基本关系,判断四个选项即可.
本题考查三角函数的诱导公式,同角三角函数基本关系,属于基础题.
10.【答案】ACD
【解析】解:∵函数f(x)=4x−14x+1−a⋅2x,
∴当a=0时,f(x)=4x−14x+1=1−24x+1为R上的增函数,且当x→−∞时,f(x)→−1,当x→+∞时,f(x)→1,即f(x)∈(−1,1),故A正确,B错误;
当a=1时f(x)=4x−14x+1−2x,f(−x)=4−x−14−x+1−2−x=1−4x4x+1−2x=−f(x),即f(x)是奇函数,故C正确;
若f(x)的定义域为R,则4x+1−a⋅2x>0恒成立,①,或4x+1−a⋅2x<0恒成立,②
解①得:a<2x+12x恒成立,
∵2x+12x≥2 2x⋅12x=2,当且仅当2x=12x,即x=0时取等号,
∴a<2;
解②得:a>2x+12x恒成立,由于当x→+∞时,2x+12x→+∞,故a不存在;
综上所述,若f(x)的定义域为R,则a<2,故D正确;
故选:ACD.
当a=0时,f(x)=4x−14x+1=1−24x+1,可分析其单调性与值域,从而可判断A、B的正误;
当a=1时,利用奇函数的定义可判断C的正误;由4x+1−a⋅2x>0恒成立,①,或4x+1−a⋅2x<0恒成立,②可判断D的正误.
本题考查函数的奇偶性与单调性的综合应用,考查转化与化归思想及综合运算能力,属于中档题.
11.【答案】ACD
【解析】解:根据题意,依次分析选项:
由f(−x)=2−x−11+2−x=1−2x2x+1=−f(x)且x∈R,则f(x)是奇函数,A对;
由f(x)=1−21+2x,函数y=1+2x在R上为增函数,易知f(x)在R上是增函数,C对;
由g(1)=[f(1)]=[1−23]=0,g(−1)=[f(−1)]=[1−43]=−1,显然g(−1)≠−g(1),B错;
当x≥0时,1+2x≥2,则f(x)=1−21+2x∈[0,1),此时g(x)=0;
当x<0时,1<1+2x<2,则f(x)=1−21+2x∈(−1,0),此时g(x)=−1;
所以g(x)的值域是{−1,0},D对.
故选:ACD.
根据题意,利用奇偶性定义及特殊值法判断A、B;根据指数函数、复合函数的单调性判断C,由函数新定义及分式型函数、指数函数性质求g(x)的值域判断D,综合可得答案.
本题考查函数的单调性与奇偶性的综合应用,熟练掌握分离常数法,指数运算及指数函数的图象与性质是解题的关键,属于中档题.
12.【答案】AC
【解析】解:当a>0时,令f(x)=t,由f(t)+1=0,即f(t)=−1,
解得t=1e或t=e或t=−2a,
作出函数f(x)的图象,如图1所示,则t=1e有一解,t=e无解,t=−2a有三解,
故f(x)=t有4个不同的实数解,
即当a>0时,g(x)有4个零点,故A正确,B错误;
当a<0时,令f(x)=t,所以f(t)+1=0,即f(t)=−1,
解得t=1e或t=e或t=−2a,由t=−2a>0,故舍去,
作出函数f(x)的图象,如图2所示,则t=1e无解,t=e有一解,
故f(x)=t有1个实数解,
即当a<0时,g(x)有1个零点,故C正确,D错误.
故选:AC.
先求得a>0时g(x)零点个数判断选项AB,再求得a<0时g(x)零点个数判断选项CD.
本题考查了分段函数的性质、分类讨论思想、数形结合思想,作出图象是关键,属于中档题.
13.【答案】(0,e]
【解析】解:函数f(x)= 1−lnx的定义域为:
{x|x>01−lnx≥0},
解得0
函数f(x)= 1−lnx的定义域为:{x|x>01−lnx≥0},由此能求出结果.
本题考查对数函数的图象和性质,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
14.【答案】3
【解析】解:设扇形的半径为r,则由扇形的面积公式可得12r2×43π=6π,
可得r=3.
故答案为:3.
直接由扇形的面积公式S=12r2θ得出即可.
本题主要考查了扇形的面积公式的应用,属于基础题.
15.【答案】a1+3a
【解析】解:因为0.3a=2,所以a=lg0.32,
因为lg2.42=+3lg0.32=a1+3a.
故答案为:a1+3a.
根据指数对数互化公式,换底公式和对数运算公式求解.
本题考查对数的运算性质,属于基础题.
16.【答案】(−4,−3]
【解析】解:方程f(x)=k有3个实数解,等价于函数y=f(x)的图象与直线y=k有3个公共点,
因当x≤0时,f(x)在(−∞,−1]上单调递减,在−1,0]上单调递增,f(−1)=−4,f(0)=−3,当x>0时,f(x)单调递增,f(x)取一切实数,
在同一坐标系内作出函数y=f(x)的图象及直线y=k,如图:
由图象可知,当−4
故答案为:(−4,−3].
根据给定条件将方程f(x)=k的实数解问题转化为函数y=f(x)的图象与直线y=k的交点问题,再利用数形结合思想即可作答.
本题考查了函数的零点与方程的根的关系,注意数形结合思想的运用,属于中档题.
17.【答案】解:(1)原式=|π−134|+[(47)2]−12+[(−2)3]23+(23)14×214+(π−2)33
=134−π+(47)−1+(−2)2+234×214+(π−2)
=134+74+4=9;
(2)原式=12lg25+lg2−lg 0.1−lg29×lg32=lg5+lg2−lg10−12−2lg23×lg32
=lg(5×2)+12−2×lg3lg2×lg2lg3
=1+12−2=−12.
【解析】(1)利用分数指数幂的运算性质运算即可.
(2)利用对数的运算性质运算即可.
本题考查指数运算,对数运算,属于基础题.
18.【答案】解:(1)sin2α−2cs2α=sin2α−2cs2α1=sin2α−2cs2αsin2α+cs2α=tan2α−2tan2α+1=25.
(2)因为tanα=2,π<α<3π2,可得5π4<α<3π2,
所以csα>sinα,则sinα−csα<0,
因为(sinα−csα)2=1−2sinαcsα=1−2sinαcsαsin2α+cs2α=1−2tanαtan2α+1=1−45=15,
所以sinα−csα=− 55.
【解析】(1)应用平方关系作“1”的代换,化为含正余弦的齐次式,再由弦化切求值;
(2)由题设5π4<α<3π2,进而得到sinα−csα<0,再应用平方关系得到齐次式,最后由弦化切求值.
本题主要考查了同角三角函数关系式的应用,属于基础题.
19.【答案】解:(1)∵函数f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=2x+1,
∴f(−x)+g(−x)=f(x)−g(x)=2−x+1,
解得:f(x)=2x+2−x,g(x)=2x−2−x;
(2)∵对任意x∈[1,+∞),不等式f(2x)≥mg(x)−2恒成立,
∴22x+2−2x≥m(2x−2−x)−2恒成立,即(2x−2−x)2+2≥m(2x−2−x)−2恒成立,
令t=2x−2−x,x∈[1,+∞),则t≥32,
也就是m≤t2+4t=t+4t对任意t∈[32,+∞)恒成立,
由基本不等式可得,t+4t≥2 t⋅4t=4,当且仅当t=4t,即t=2时等号成立,
∴m≤4.
即实数m的最大值为4.
【解析】(1)由已知可得f(−x)+g(−x)=f(x)−g(x)=2−x+1,与原式联立即可求得f(x)与g(x);
(2)问题转化为(2x−2−x)2+2≥m(2x−2−x)−2恒成立,令t=2x−2−x,则t≥32,即m≤t2+4t=t+4t对任意t∈[32,+∞)恒成立,再由基本不等式求最值,即可得到实数m的最大值.
本题考查函数解析式的求解及常用方法,考查化归与转化思想,训练了利用基本不等式求最值,是中档题.
20.【答案】解:(1)由P=P0e−kt可知,当t=0时,P=P0,
当t=5时,P=(1−10%)P0,则有P0e−5k=(1−10%)P0,
解得k=−15ln0.9,
所以P=P0e(15ln0.9)t=P00.9t5,
故当t=10时,P=P00.92=0.81P0,
即10h后还剩81%的污染物.
(2)要使污染物减少三分之一以上,则有P≤23P0,P00.9t5≤23P0,
因为P0>0,所以0.9t5≤23,
t5≥lg0.923=ln2−ln32ln3−ln2−ln5=0.69−1.12.2−0.69−1.61=4.1,
所以t≥20.5,
故要使污染物减少三分之一以上至少需要21小时.
【解析】(1)将数学应用问题抽象出指数函数的模型,代入已知条件所给指数型的函数即可求解.
(2)要使污染物减少三分之一以上,则P≤23P0,根据指对互换和已知所给数据求解即可.
本题考查函数模型的运用,考查学生的计算能力,属于中档题.
21.【答案】解:(1)因为函数为偶函数,所以f(−x)=f(x),
而f(x)=lg3(3x+1)−kx,所以f(−x)=lg3(3−x+1)+kx,,
即lg3(3x+1)−kx−[lg3(3−x+1)+kx]=0,整理可得lg33x+13−x+1−2kx=0,即lg33x−2kx=0,
可得(1−2k)x=0恒成立,所以k=12,
所以f(x)=lg3(3x+1)−12x;
(2)由(1)可得g(x)=f(x)+12x=lg3(3x+1),在x∈[lg32,8]上单调递增,
由题意可得存在x1∈[lg32,8],g(x1)min=lg3(3lg32+1)=lg33=1,
存在x1∈[lg32,8],对任意的x2∈[1,4],都有g(x1)≤h(x2),可得g(x1)min≤h(x2)min,
即h(x2)min=1,
而h(x)=x2−2tx+5,开口向上,对称轴为x=t,x∈[2,8],
(i)当t≥4时,h(x)在x∈[1,4]上单调递减,所以h(4)为最小值,且h(4)=16−4t+5=21−4t,
则需21−4t≥1,可得t≤5,
此时4≤t≤5;
(ii)当t≤1时,则h(x)在x∈[1,4]上单调递增,所以h(1)为最小值,且h(1)=1−2t+5=6−2t,
可得6−2t≥1,解得t≤52,
所以此时t≤1;
(iii)当1
此时1
【解析】(1)由偶函数可得f(−x)=f(x),可得k的值,进而求出函数f(x)的解析式;
(2)由(1)可得函数g(x)的解析式;再由题意满足g(x1)min≤h(x2)min即可,求出g(x1)min,分类讨论h(x2)的最小值,求出t的范围.
本题考查偶函数性质的应用,存在命题的性质的应用,分类讨论方法的应用,属于中档题.
22.【答案】解:(1)当λ=2时,f(x)=lg2x+1x,
由lg2x+1x>0,得2x+1x>1⇒2x+1x−1>0,
即x+1x>0,等价于(x+1)x>0,
解得x∈(−∞,−1)∪(0,+∞);
(2)因为对任意x1,x2∈[a,a+1],都有|f(x1)−f(x2)|≤lg2,
所以对任意x1,x2∈[a,a+1],都有f(x)max−f(x)min≤lg2,
设f(x)的定义域为I,
又当x1,x2∈I且x1
即f(x1)>f(x2),所以f(x)在I上单调递减.
因此函数f(x)在区间[a,a+1]上的最大值与最小值分别为f(a),f(a+1).
由f(a)−f(a+1)=lg(λa+1a)−lg(λa+λ+1a+1)≤lg2,
化简得λa2+(λ+1)a−1≥0,
上式对任意a∈[12,2]成立.
因为λ>0,Δ=(λ+1)2+4λ>0,
令h(a)=λa2+(λ+1)a−1,对称轴为a=−λ+12λ<0,
所以函数h(a)=λa2+(λ+1)a−1在区间a∈[12,2]上单调递增,
所以,h(a)min=h(12)=34λ−12,
由34λ−12≥0,得λ≥23.
故λ的取值范围为[23,+∞).
【解析】(1)将λ=2代入函数,再由对数函数的性质求解即可;
(2)由题意可得f(x)max−f(x)min≤lg2,先判断出函数f(x)在定义域上为单调递减函数,进而得f(a)−f(a+1)≤lg2,即得λa2+(λ+1)a−1≥0,对任意a∈[12,2]成立,结合二次函数的性质求出h(a)=λa2+(λ+1)a−1在区间a∈[12,2]的最小值即可求得λ的取值范围.
本题主要考查函数恒成立问题,考查不等式解法,考查运算求解能力,属于中档题.
2023-2024学年广西柳州重点中学高一(上)期末数学试卷(含解析): 这是一份2023-2024学年广西柳州重点中学高一(上)期末数学试卷(含解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年山东省济南市高二(上)期末数学模拟试卷(含解析): 这是一份2023-2024学年山东省济南市高二(上)期末数学模拟试卷(含解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年安徽省阜阳市高一(上)期末数学模拟试卷(含解析): 这是一份2023-2024学年安徽省阜阳市高一(上)期末数学模拟试卷(含解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












