广东省东莞市重点中学2023-2024学年八年级上学期数学期末试题(无答案)

这是一份广东省东莞市重点中学2023-2024学年八年级上学期数学期末试题(无答案)，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
说明：本试卷共120分，本次考试120分钟。
一、选择题（本大题共10小题，每小题3分，共30分。每小题只有一个选项符合题意）
1.下列图案是轴对称图形的有（ ）个
A.1B.2C.3D.4
2.某种生物孢子的直径为，用科学记数法表示为（ ）
A.B.C.D.
3.给出下列计算，其中正确的是（ ）
A.B.C.D.
4.若使分式有意义，则的取值范围是（ ）
A.B.C.D.
5.（ ）
A.3B.C.D.
6.如图，，为的中点，以下结论正确的有几个？（ ）
①；②；③；④是的角平分线.
A.1B.2C.3D.4
7.如图，工人师傅砌门时，常用木条固定长方形门框，使其不变形，这样做的根据是（ ）
A.两点之间的线段最短B.长方形的四个角都是直角
C.长方形是轴对称图形D.三角形有稳定性
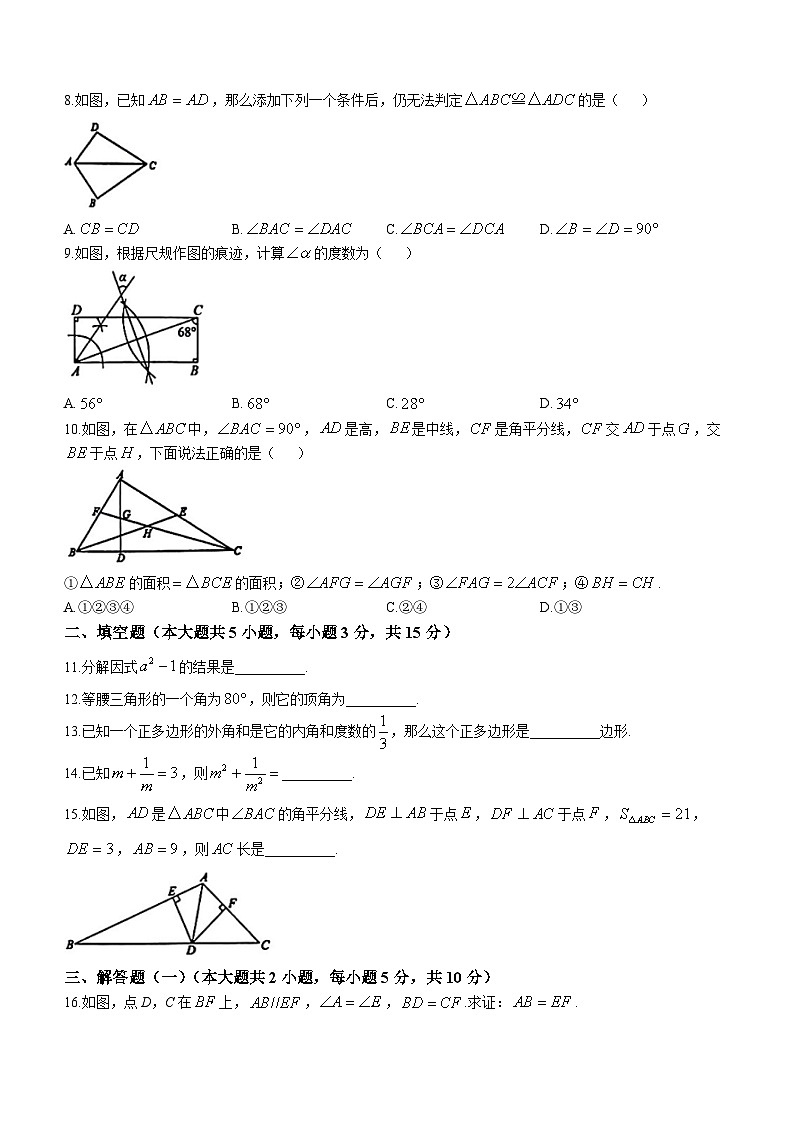
8.如图，已知，那么添加下列一个条件后，仍无法判定的是（ ）
A.B.C.D.
9.如图，根据尺规作图的痕迹，计算的度数为（ ）
A.B.C.D.
10.如图，在中，，是高，是中线，是角平分线，交于点，交于点，下面说法正确的是（ ）
①的面积的面积；②；③；④.
A.①②③④B.①②③C.②④D.①③
二、填空题（本大题共5小题，每小题3分，共15分）
11.分解因式的结果是__________.
12.等腰三角形的一个角为，则它的顶角为__________.
13.已知一个正多边形的外角和是它的内角和度数的，那么这个正多边形是__________边形.
14.已知，则__________.
15.如图，是中的角平分线，于点，于点，，，，则长是__________.
三、解答题（一）（本大题共2小题，每小题5分，共10分）
16.如图，点D，C在上，，，.求证：.
17.计算：.
四、解答题（二）（本大题共3小题，每小题7分，共21分）
18.如图，三个顶点的坐标分别为，，.
（1）画出关于轴的对称图形，并写出点的坐标；
（2）在轴上求作一点，使的周长最小，并直接写出点的坐标.
19.如图，在中，，，求的度数.
20.一个等屋三角形的周长为.
（1）已知腰长是底边长的2倍，求各边的长；
（2）已知其中一边的长为.求其它两边的长.
五、解答题（三）（本大题共3小题，每小题8分，共24分）
21.先化简再求值，其中.
22.如图，中，，，的垂直平分线交于点，交于点，，求的长.
23.某校在商场购进A、B两种品牌的篮球，购买A品牌篮球花费了2500元，购买B品牌篮球花费了2000元，且购买A品牌篮球的数量是购买B品牌篮球数量的2倍，已知购买一个B品牌篮球比购买一个A品牌篮球多花30元.
（1）问购买一个A品牌、一个B品牌的篮球各需多少元？
（2）该校决定再次购进A、B两种品牌篮球共50个，恰逢商场对两种品牌篮球的售价进行调整，A品牌篮球售价比第一次购买时提高了，B品牌篮球按第一次购买时售价的9折出售，如果该校此次购买A、B两种品牌篮球的总费用不超过3060元，那么该校此次最多可购买多少个B品牌篮球？
六、解答题（四）（本大题共2小题，每小题10分，共20分）
24.已知为等边三角形，点为直线上一动点（点不与点，点重合）.以为边作等边三角形，连接.
图1图2
（1）如图1，当点在边上时.
①求证：；
②求证：；
（2）如图2，当点在边的延长线上时，其他条件不变，请写出，，之间存在的数是关系，并写出证明过程.
25.如图1，点P、Q分别是长为的等边三角形的边、上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为.
图1图2
（1）连接、交于点，则在P、Q运动的过程中，变化吗？若变化，则说明理由，若不变，则求出它的度数；
（2）P、Q运动几秒时，是直角三角形？
（3）如图2，若点P、Q在运动到终点后继续在射线、上运动，直线、交点为，则变化吗？若变化说明理由，若不变，则求出它的度数.