人教A版 (2019)必修 第二册第六章 平面向量及其应用6.2 平面向量的运算说课课件ppt

这是一份人教A版 (2019)必修 第二册第六章 平面向量及其应用6.2 平面向量的运算说课课件ppt，共21页。PPT课件主要包含了导入新课，精彩课堂，课堂练习，课堂总结等内容，欢迎下载使用。

6.2.4 向量的数量积第1课时 向量的数量积
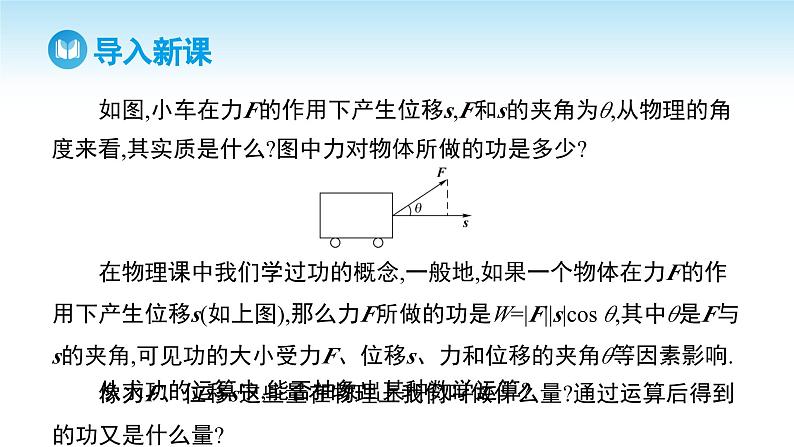
如图,小车在力F的作用下产生位移s,F和s的夹角为θ,从物理的角度来看,其实质是什么?图中力对物体所做的功是多少?
在物理课中我们学过功的概念,一般地,如果一个物体在力F的作用下产生位移s(如上图),那么力F所做的功是W=|F||s|cs θ,其中θ是F与s的夹角,可见功的大小受力F、位移s、力和位移的夹角θ等因素影响.
像力F、位移s这些量在物理上我们叫做什么量?通过运算后得到的功又是什么量?
从求功的运算中,能否抽象出某种数学运算?
1.两个向量的夹角
观察力做功的计算公式,发现公式中涉及力与位移的夹角,所以先来定义向量夹角的概念.阅读教材,看一看,如何定义向量a与b的夹角?两个非零向量的夹角的范围是什么?
2.向量的数量积
阅读教材,看看向量的数量积是如何定义的,其运算的结果是向量吗?向量的数量积与哪些量有关?
向量的数量积的定义 已知两个非零向量a与b,它们的夹角为θ,我们把数量|a||b|cs θ叫做向量a与b的数量积(或内积),记作a·b,即a·b=|a||b|cs θ. 规定:零向量与任一向量的数量积为0.
向量的线性运算的结果是一个向量, 而两个向量的数量积是一个数量, 这个数量的大小与两个向量的长度及其夹角有关.
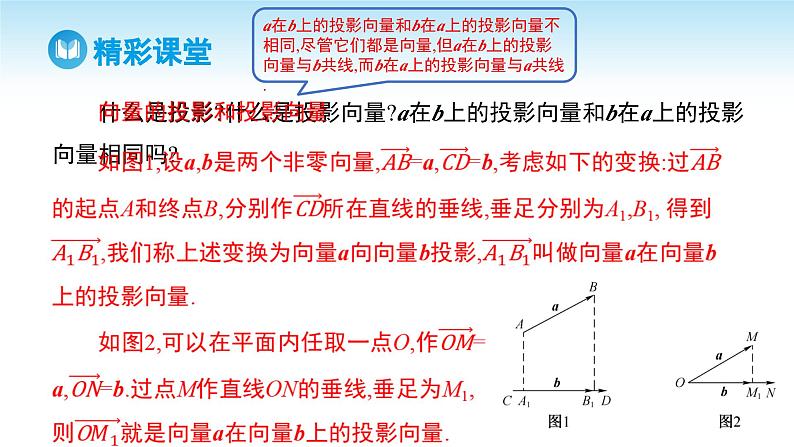
什么是投影?什么是投影向量?a在b上的投影向量和b在a上的投影向量相同吗?
a在b上的投影向量和b在a上的投影向量不相同,尽管它们都是向量,但a在b上的投影向量与b共线,而b在a上的投影向量与a共线.
【提示】分θ为锐角、直角、钝角以及θ=0,θ=π等情况进行讨论.
a·b几何意义是什么?
a·b可以看成是a在b上的投影向量与b的数量积.
3.向量数量积的性质
设a,b是非零向量,它们的夹角是θ,e是与b方向相同的单位向量,那么a·e与e·a之间有什么关系?
a·e=|a||e|cs θ=|a|cs θ,e·a=|e||a|cs θ=|a|cs θ=a·e.
从上面的探究我们看到,两个非零向量a与b相互平行或垂直时,向量a在向量b上的投影向量具有特殊性.这时,它们的数量积又有怎样的特殊性?
a·a常常记作a2.
借助刚才的探究结果,你认为a·b的取值范围是什么?能否给出你的判断依据?
因为0≤θ≤180°, 所以－1≤cs θ≤1, 所以－|a||b|≤a·b≤|a||b|, 即|a·b|≤|a||b|.
4.应用举例
在求解时,要注意θ的取值范围.
1.本节课学习的主要内容是什么?2.平面向量的数量积有哪些应用?3.我们是按照怎样的思维模式进行概念的归纳和性质的探究的?4.类比向量的线性运算, 还可以怎样研究向量的数量积?