高中数学第九章 统计9.2 用样本估计总体课文配套ppt课件

这是一份高中数学第九章 统计9.2 用样本估计总体课文配套ppt课件，共27页。PPT课件主要包含了导入新课，精彩课堂，引申关联，课堂练习，课堂总结等内容，欢迎下载使用。

9.2.4 总体离散程度的估计
1.利用频率分布直方图估计样本数据的众数、中位数、平均数的方法.平均数的求法:每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.中位数的求法:根据中位数左边和右边矩形面积和均为0.5,列式求解.众数的求法:最高矩形所在区间的中点.2.平均数、中位数、众数在数据分析中有什么作用?平均数、中位数、众数提供了数据集中趋势的信息.
1.总体离散程度的初步判断问题1 有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲 7 8 7 9 5 4 9 10 7 4乙 9 5 7 8 7 6 8 6 7 7如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
两组数据的平均数、中位数、众数都是7.
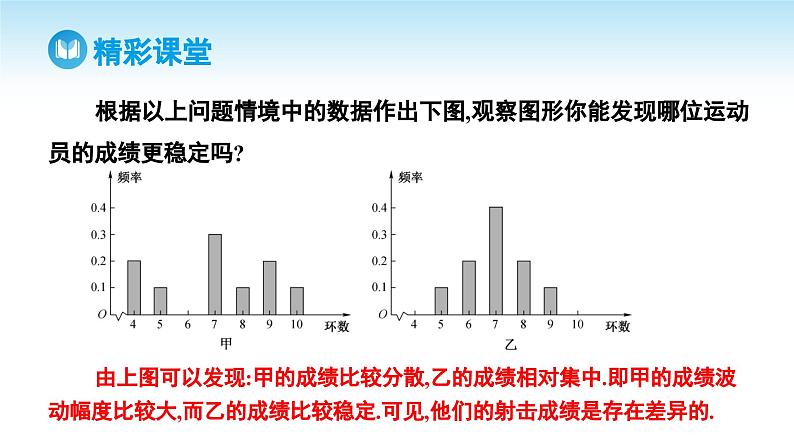
根据以上问题情境中的数据作出下图,观察图形你能发现哪位运动员的成绩更稳定吗?
由上图可以发现:甲的成绩比较分散,乙的成绩相对集中.即甲的成绩波动幅度比较大,而乙的成绩比较稳定.可见,他们的射击成绩是存在差异的.
问题2 问题1中,甲、乙的射击成绩的平均数、中位数、众数相同,但二人的射击成绩稳定性存在差异.那么,如何度量这种差异呢?可以利用极差进行度量.根据上述数据计算得:甲命中环数的极差= 10-4=6,乙命中环数的极差=9-5=4,极差在一定程度上刻画了数据的离散程度.由极差发现甲的成绩波动范围比乙的大.
由于极差只使用了数据中最大、最小两个值的信息,故所含的信息量很少.也就是说,极差度量出的差异误差较大.
你能想出其他刻画数据离散程度的办法吗?如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远.因此,可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度.
为什么用“平均距离”刻画离散程度?用“总距离”行吗?例如,从一个总体中抽取两组样本,但两组的样本量不同,一个为100,另一个为1 000,如果用“总距离”,两者之间会相差很大,但“平均距离”相差不大,所以我们用“平均距离”来刻画离散程度.
问题4 方差和标准差各指什么?
问题5 标准差的范围是什么?标准差为0的一组数据有什么特点?
当需要比较两组数据离散程度大小的时候,如果两组数据的测量尺度相差太大,或者数据量纲不同,直接使用标准差来进行比较是不合适的.此时应当消除测量尺度和量纲的影响,而变异系数可以做到这一点,它是原始数据标准差与原始数据平均数的比.变异系数没有量纲,这样就可以进行客观比较了.
问题6 标准差和方差是怎样刻画数据的离散程度的?标准差和方差刻画了数据的离散程度或波动幅度.标准差(或方差) 越大,数据的离散程度越大,越不稳定;标准差(或方差) 越小,数据的离散程度越小,越稳定.显然,在刻画数据的分散程度上,方差和标准差是一样的.但在实际问题中,一般多采用标准差.在实际问题中,总体平均数和总体标准差都是未知的,就像用样本平均数估计总体平均数一样,通常也用样本标准差估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
对于问题1,可以根据标准差来判断两名运动员的成绩的离散程度,计算可得s甲=2,s乙≈1.095.由s甲>s乙可知,甲的成绩离散程度大,乙的成绩离散程度小.由此可以估计,乙比甲的射击成绩稳定.如果要从这两名选手中选择一名参加比赛,要看一下他们的平均成绩在所有参赛选手中的位置.如果两人都排在前面,就选成绩稳定的乙选手,否则可以选甲.
3.求由样本量比例分配的分层随机抽样获取的数据的方差