2020-2021学年山西省吕梁市交城县八年级上学期期中数学试题及答案

这是一份2020-2021学年山西省吕梁市交城县八年级上学期期中数学试题及答案，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

给出下列说法：①等边三角形是等腰三角形；②三角形按边的相等关系可分为等腰三角形、等边三角形和三边都不相等的三角形；③三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中正确的有
A.0个 B.1个 C.2个 D.3个
2.下列长度的3根小木棒不能搭成三角形的是
A.2cm，3cm，4cm B.1cm，2cm，3cm
C.3cm，4cm，5cm D.4cm，5cm，6cm
下列图形中AD是△ABC的高的是
已知直角三角形ABC中，有一个锐角等于50°，则另一个锐角的度数是
A.50° B.45° C.40° D.30°
5. 如图，在ΔABC中，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E.若∠A=54°，∠B=46°，则∠CDE的度数为
A.45° B.40° C.39° D.35°
6. 如图，已知AD=AE,BE=CD,∠1=∠2=100°,若∠BAE=60°,则∠CAE的度数为
A. 40° B. 60° C.80° D. 100°
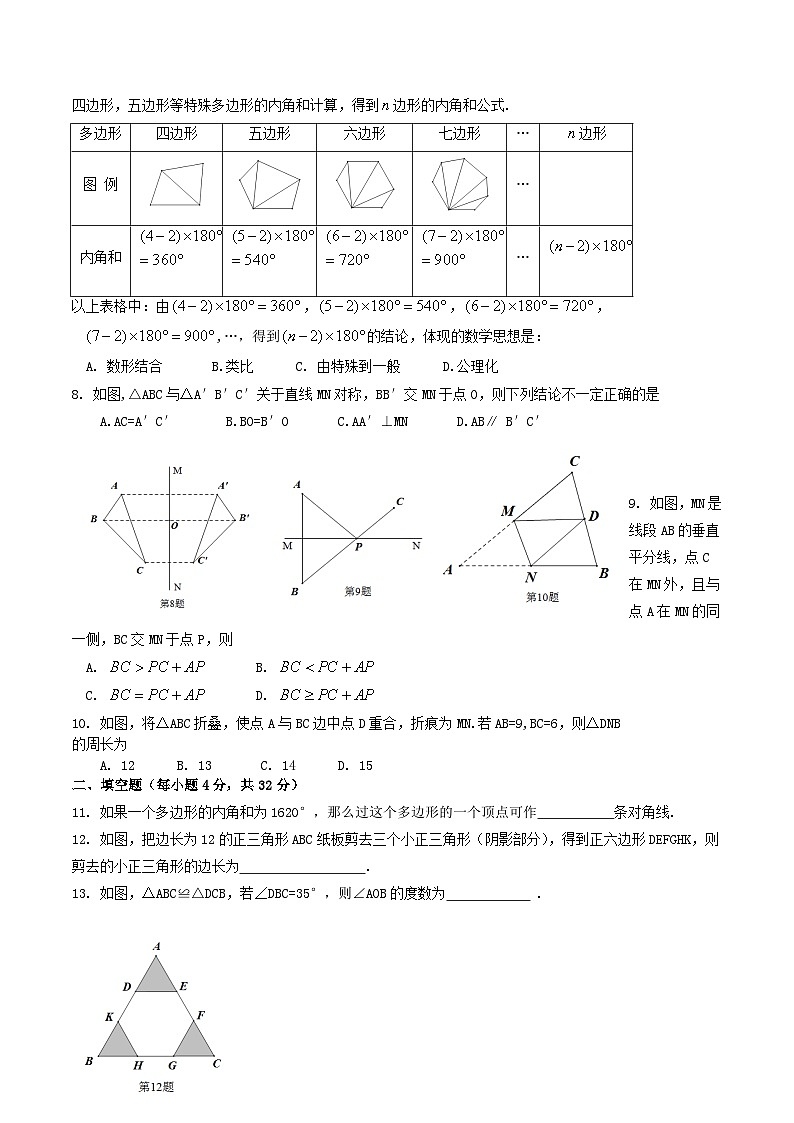
7.在探索多边形内角和公式的过程中，多数同学采用如下表格中分割多边形的方法，并从
四边形，五边形等特殊多边形的内角和计算，得到边形的内角和公式.
以上表格中：由，，，,…，得到的结论，体现的数学思想是：
A. 数形结合 B.类比 C. 由特殊到一般 D.公理化
8. 如图,△ABC与△A′B′C′关于直线MN对称，BB′交MN于点O，则下列结论不一定正确的是
A.AC=A′C′ B.BO=B′O C.AA′⊥MN D.AB∥ B′C′
9. 如图，MN是线段AB的垂直平分线，点C在MN外，且与点A在MN的同一侧，BC交MN于点P，则
A. B.
C. D.
10. 如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN.若AB=9,BC=6，则△DNB
的周长为
A. 12 B. 13 C. 14 D. 15
二、填空题（每小题4分，共32分）
11. 如果一个多边形的内角和为1620°，那么过这个多边形的一个顶点可作 条对角线.
12. 如图，把边长为12的正三角形ABC纸板剪去三个小正三角形（阴影部分），得到正六边形DEFGHK，则剪去的小正三角形的边长为 .
13. 如图，△ABC≌△DCB，若∠DBC=35°，则∠AOB的度数为 .


14.如图，AB=AC，BE=CD，要使△ABE≌△ACD，依据“SSS”，则还需添加条件 .（填一个即可）
15.已知两点的坐标分别是（-2,3）和（2,3），给出下列说法：①两点关于轴对称；②两点关于轴对称；③两点之间的距离为4.其中正确的是 .（填序号）
16.如图，AB⊥CD，且AB=CD，E，F是AD上两点，CF⊥AD，BE⊥AD.若CF=8，BE=6，AD=10，则EF的长为 .
17.如图，在△ABC中，AB=AC=10,BC=12,AD=8,AD是∠BAC的平分线.若E是AC上一点且BE⊥AC，P是AD的动点，则PC+PE的最小值是 .
已知O为等边三角形ABD的边BD的中点，AB=4，E,F分别为射线AB，DA上一动点，且∠EOF=120°，若AF=1，则BE的长为 .
三、解答题（共58分）
19.（第1小题6分，第2小题12分，共18分）
（1）（6分）如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分.（不写已知、求作、作法，只保留作图痕迹）
（12分）如图，已知△ABC在平面直角坐标系中的位置如图所示.
①作出△ABC关于轴对称的,并写出各顶点的坐标；
②将△ABC向右平移6个单位长度，作出平移后的，并写出各顶点的坐标；
③观察与，它们是否关于某条直线对称？若是，请在图上画出这条对称轴.
(8分)如图，在四边形ABCD中，E是CB的中点，延长AE，DC相交于点F，∠CEA=∠B+∠F.求证：AB=FC.
（10分）如图，已知△ABC为等边三角形，D为BC延长线上一点，CE平分∠ACD，CE=BD.求证：△ADE为等边三角形.
（10分）如图，在Rt△ABC中，∠BAC=90°，∠ABC=60°,AD,CE分别平分∠BAC，∠ACB,AD与CE交于点O，连接OB.
（1）若OF⊥AC于点F,AB=4,OF=.求△BOC的面积；
（2）求证：AC=AE+CD.
23.（12分）综合探究:探索等腰三角形中相等的线段
问题情境：
数学活动课上，老师提出了一个问题：等腰三角形底边中点到两腰的距离相等吗？同学们就这个问题展开探究.
问题初探：
希望小组的同学们根据题意画出了相应的图形，如图1.在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为点E，F.经过合作，该小组的同学得出的结论是DE=DF.并且展示了他们的证法如下：
证明：如图1，
∵DE⊥AB，DF⊥AC
∴∠DEB=∠DFC=90°
∵AB=AC
∴∠B=∠C（依据1）
∵D是BC的中点
∴BD=CD
在△BDE和△CDF中
∴△BDE≌△CDF（依据2）
∴DE=DF
①请写出依据1和依据2的内容
依据1： .
依据2： .
②请你应用图2写出一种不同于希望小组的证法.
问题再探：
未来小组的同学经过探究又有新的发现，如果在等腰三角形ABC中，作腰AB上的高CG，如图3.则CG与DE有确定的数量关系.请你直接写出这个数量关系为 .
类比探究：
（3）奋斗小组的同学认真研究过后，发现了以下两个正确结论：①在图4中，若DE，DF分别为△ABD和△ACD的中线，那么DE=DF仍然成立；②在图5中，若DE，DF分别为△ABD和△ACD的角平分线，那么DE=DF仍然成立.请你选择其中一个结论，写出证明过程.
八年级数学上册期中测试题答案
一、选择题
1—5 C B D C B 6—10 A C D C A
二、填空题
11. 8 12. 4 13. 70 14. AE=AD（CE=BD） 15. ②③
16. 4 17. 18. 3或1
三、解答题
19. 共20分 （1）（6分）图略
（2）（12分）①图略（图2分，坐标各1分，共5分）（0,4）,（2,2）, (1，1)
②图略（图2分，坐标各1分，共5分）（6,4）,（4,2）, (5，1)
③图略（2分）
20.证明：∵∠CEA=∠B+∠EAB
∠CEA=∠B+∠F
∴∠EAB=∠F ………………………… 3分
∵E是CB的中点
∴BE=CE ………………………… 5分
在△ABE与△FCE中

∴△ABE≌△FCE(AAS) ………………………… 7分
∴AB=FC ………………………… 8分
21.证明：∵△ABC是等边三角形
∴AB=AC,∠B=∠BAC=∠ACB=60°………………………… 2分
∴∠ACD=120°
∵CE平分∠ACD
∴∠ACE=60° ………………………… 3分
∴∠B=∠ACE ………………………… 4分
在△ABD与△ACE中

∴△ABD≌△ACE(SAS) ……………………6分
∴AD=AE,∠BAD=∠CAE ……………………8分
∴∠BAD-∠CAD=∠CAE-∠CAD
即∠BAC=∠DAE=60° ……………………9分
∴ △ADE是等边三角形 ……………………10分
22.（第一问4分，第二问6分，共10分）
证明：(1)作OG⊥BC，垂足为G ……………………… 1分
∵∠BAC=90°,∠ABC=60°
∴ ∠ACB=30°
∴BC=2AB=8 …………………………2分
∵CE平分∠ACB,OF⊥AC,OG⊥BC
∴OG=OF= ………………………… 3分
∴…………………… 4分
在AC上截取AH=AE………………5分
∵AD平分∠BAC,CE平分∠ACB
∴∠1=∠2=45°,∠3=∠4=15°
∴∠AOE=60°
在△EAO与△HAO中

∴△EAO≌△HAO(SAS) ……………………… 6分
∴∠AOE=∠AOH=60°
∵∠AOE=60°
∴ ∠AOC=120°,∠COD=60°
∴∠COH=∠COD=60°……………………… 7分
∵CE平分∠ACB
∴∠3=∠4
在△COD与△COH中

∴△COD≌△COH(ASA) ……………………… 8分
∴CD=CH………………………… 9分
∵AC=AH+CH
∴AC=AE+CD………………………… 10分
23.（第一问6分，①各1分，②4分，第二问2分，第三问4分，共12分）
（1）①依据1：等腰三角形的两个底角相等或等边对等角 ………………… 1分
依据2：两角分别相等且其中一组等角的对边相等的两个三角形全等或角角边或AAS ………………… 2分
②（4分）答案不唯一，如
连接AD ………………… 3分
∵AB=AC,D是BC的中点
∴AD是∠BAC的平分线 ………………… 5分
∵DE⊥AB,DF⊥AC
∴DE=DF ………………… 6分
(2)（2分）CG=2DE …………………… 8分
(3)(4分)
选择①证明：∵DE，DF是△ABD和△ACD的中线
∴BE=AB，CF=AC ………………………… 9分
∵AB=AC
∴BE=CF,∠B=∠C ………………………… 10分
又∵D是BC的中点
∴BD=CD ………………………… 11分
在△BDE与△CDF中

∴△BDE≌△CDF(SAS)
∴DE=DF ………………………… 12分
选择②证明：∵AB=AC,D是BC的中点
∴∠B=∠C,BD=CD,AD⊥BC
∴∠ADB=∠ADC=90°………………………… 9分
又∵DE,DF分别是△ABD和△ACD的平分线
∴∠BDE=∠CDF=45°………………………… 10分
在△BDE与△CDF中

∴△BDE≌△CDF(ASA) ………………………… 11分
∴DE=DF ………………………… 12分
题号
1
2
3
4
5
6
7
8
9
10
答案
多边形
四边形
五边形
六边形
七边形
…
边形
图 例
…
内角和
…