2021-2022学年福建省龙岩市长汀县八年级下学期期中数学试题及答案

这是一份2021-2022学年福建省龙岩市长汀县八年级下学期期中数学试题及答案，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(每小题4分，共40分)
1.若在实数范围内有意义，则x的取值范是
2.下列各式中计算正确的是
3.计算：，则中的数是
4.在综合实践活动课上，小明用三根木棒首尾顺次相接摆三角形，下列每组数分别是三根木棒的长度(单位：cm)，其中能摆出直角三角形的一组是
A.32，42，52B.9，12，15C.6，7，8D.4，4，7
5.下列命题中，真命题是
A.两条对角线互相平分的四边形是平行四边形B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相垂直且相等的四边形是正方形D.两条对角线相等的四边形是矩形
6.为预防新冠疫情，民生大院入口的正上方A处装有红外线激光测温仪(如图所示)，测溢仪离地面的距离AB=2.4米米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温.当身高为1.8米的市民CD正对门缓慢走到高门0.8米的地方时(即测温仪自动显示体温，则人头顶高测温仪的距离AD等于
A.1.5米米C.1.2米D.1.0米
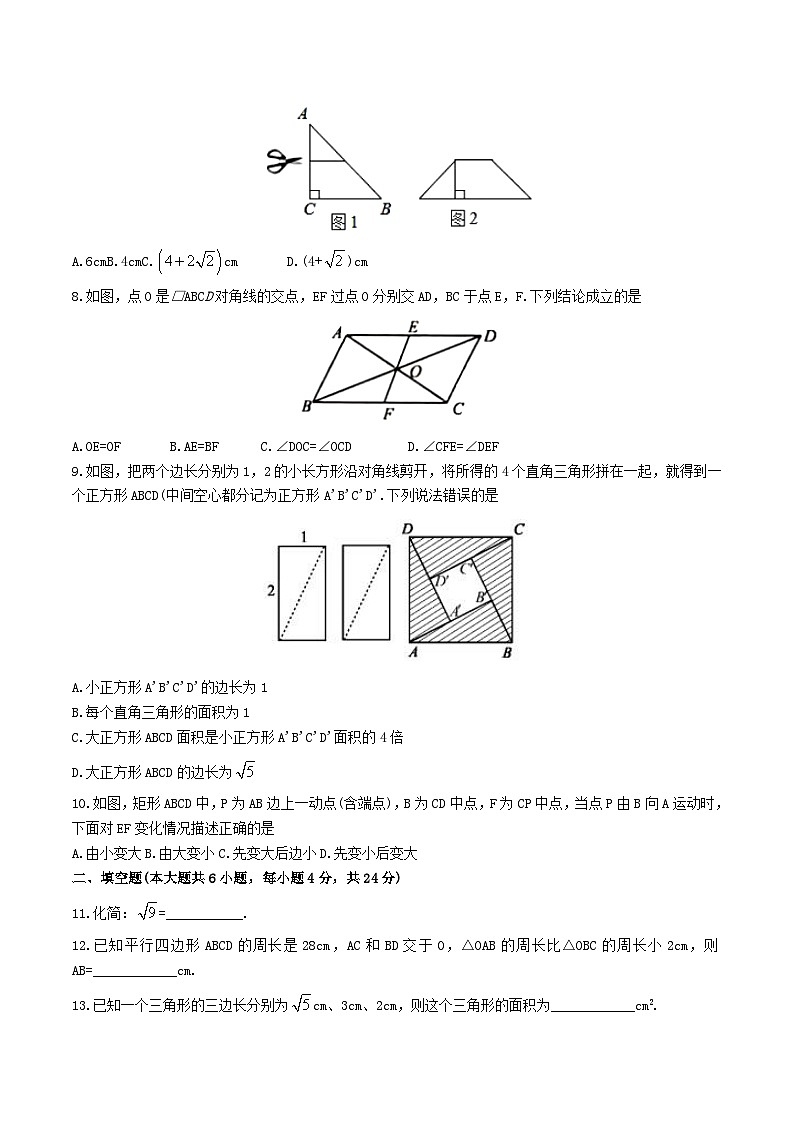
7.如图1是一张等腰直角三角形纸片，直角边的长度为2cm，用剪刀沿一直角边和斜边的中点连线(图中虚线)剪开后，拼成如图2的四边形，则该四边形的周长为
D.(4+)cm
8.如图，点O是□ABCD对角线的交点，EF过点O分别交AD，BC于点E，F.下列结论成立的是
A.OE=OF B.AE=BF C.∠DOC=∠OCD D.∠CFE=∠DEF
9.如图，把两个边长分别为1，2的小长方形沿对角线剪开，将所得的4个直角三角形拼在一起，就得到一个正方形ABCD(中间空心都分记为正方形A'B'C'D'.下列说法错误的是
A.小正方形A'B'C'D'的边长为1
B.每个直角三角形的面积为1
C.大正方形ABCD面积是小正方形A'B'C'D'面积的4倍
D.大正方形ABCD的边长为
10.如图，矩形ABCD中，P为AB边上一动点(含端点)，B为CD中点，F为CP中点，当点P由B向A运动时，下面对EF变化情况描述正确的是
A.由小变大B.由大变小C.先变大后边小D.先变小后变大
二、填空题(本大题共6小题，每小题4分，共24分)
11.化简：=___________.
12.已知平行四边形ABCD的周长是28cm，AC和BD交于0，△OAB的周长比△OBC的周长小2cm，则AB=____________cm.
13.已知一个三角形的三边长分别为cm、3cm、2cm，则这个三角形的面积为____________cm2.
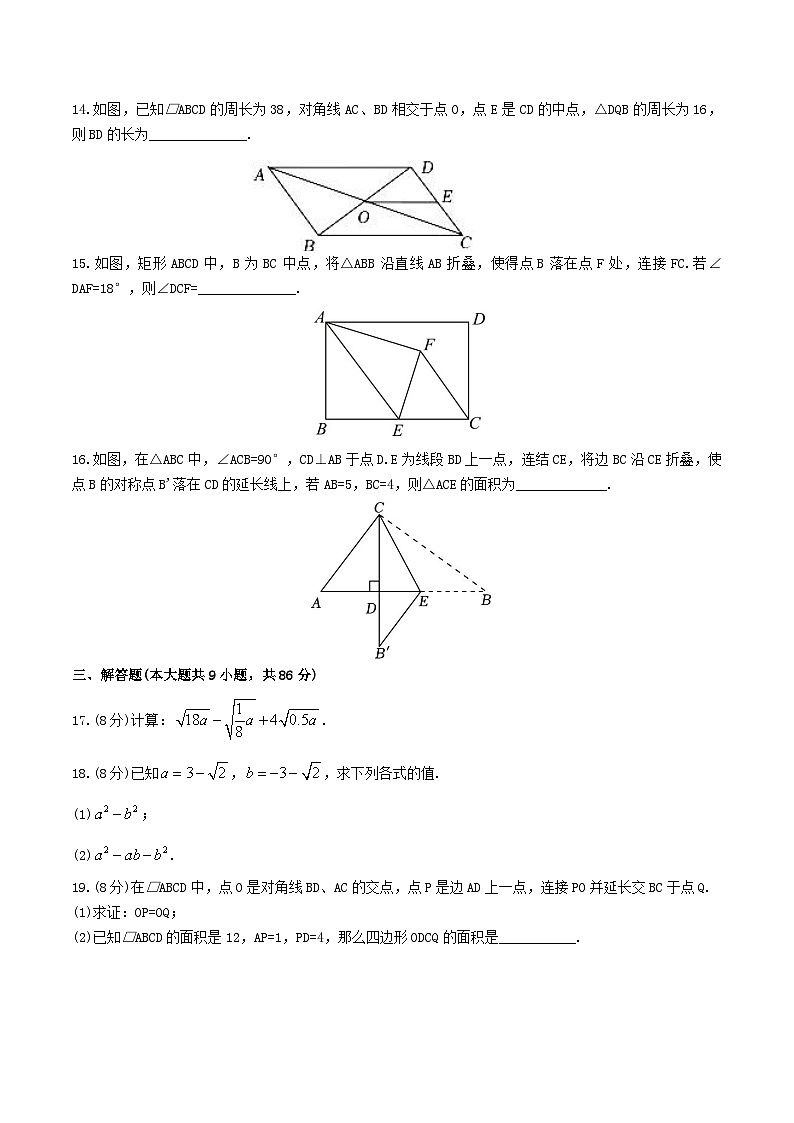
14.如图，已知□ABCD的周长为38，对角线AC、BD相交于点O，点E是CD的中点，△DQB的周长为16，则BD的长为______________.
15.如图，矩形ABCD中，B为BC中点，将△ABB沿直线AB折叠，使得点B落在点F处，连接FC.若∠DAF=18°，则∠DCF=______________.
16.如图，在△ABC中，∠ACB=90°，CD⊥AB于点D.E为线段BD上一点，连结CE，将边BC沿CE折叠，使点B的对称点B'落在CD的延长线上，若AB=5，BC=4，则△ACE的面积为_____________.
三、解答题(本大题共9小题，共86分)
17.(8分)计算：.
18.(8分)已知，，求下列各式的值.
(1)；
(2).
19.(8分)在□ABCD中，点O是对角线BD、AC的交点，点P是边AD上一点，连接PO并延长交BC于点Q.
(1)求证：OP=OQ；
(2)已知□ABCD的面积是12，AP=1，PD=4，那么四边形ODCQ的面积是___________.
20.(8分)在甲村至乙村的公路旁有一块山地正在开发，现有一C处需要爆破.已知点C与公路上的停靠站A的距离为500米，与公路上另一停靠站B的距高为1200米，且CA⊥CB如图，为了安全起见，爆破点C周围半径400米范围内不得进入，问在进行爆破时，公路AB段是否有危险，是否需要暂时封错？请通过计算进行说明.
21.(8分)如图，已知∠AOB，OA=OB，点E在边OB上，四边形AEBF是平行四边形.
(1)请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹，不写作法)
(2)请说明你的画法的正确性.
22.(10分)如图是直角三角尺(△ABC)和等原直角三角尺(△BCD)放置在同一平面内，斜边BC合在一起，∠A=∠BDC=90°，∠ABC=30°，BD=CD，DE⊥AB交AB于点E；作DF⊥AC交AC的延长线于点F.
(1)求证：四边形AEDF是正方形.
(2)当AC=4时，求正方形AEDF的边长.
23.(10分)如图，斜靠墙上的一根竹竿AB长为10m，端点B高墙角的水平距高BC长为6m.
(1)已知A端沿AC向下移动到A1，AA1=acm，B端将沿CB方向移动到B1，BB1=bcm，.
①当a=1时，求b的值；
②当时，求a的值.
(2)在竹竿滑动的过程中，△ABC面积有最_______值(填“大”或“小”)，该最值是_______cm2.
24.(12分)如果一个四边形存在一条对角线，使得这条对角线长度的平方是四边形某两边长度的乘积，则称这个四边形为“闪亮四边形”，这条对角线称为“亮线”，如图1，在这个四边形ABCD中，AB=AC=AD，满足AC2=AB×AD，四边形ABCD是内亮四边形，AC是亮线.
(1)以下说法在确的是__________(填写序号)
①正方形不可能是闪亮四边形②矩形有可能是闪亮四边形
③若一个菱形是闪亮四边形，则必有一个角为120°
(2)如图2，在四边形ABCD中，AD∥BC，∠ABC=90°，AD=9，AB=12，CD=20，四边形ABCD是否为闪亮四边形？如果是，哪条线段是亮线，并写出验证过程，如果不是，说明理由.
25.(14分)如图，在平行四边形ABCD中，点E为AC上一点，点E与点F关于CD对称.
(1)连接DE，DF，CF，已知EF与CD交于点O，ED∥CF.
①求证：四边形ECFD是菱形.
②若点E为AC的中点，求证：AD=EF；
(2)若四边形ABCD是正方形，连接BD，BE，BF，当△BDF是直角三角形时，求的值.
参考答案
参考答案及评分标准
一、选择题（本大题共10题，每题4分，共40分）
二、填空题（本大题共6题，每题4分，共24分）
11.3；12.6；13.；14.13；15.36°；16.
三、解答题（本大题共9小题，共86分）
17.（8分）计算：．
解：原式……………6分
．………………8分
18.(8分)已知，，求下列各式的值.
(1)；
(2).
解：(1)∵，
∴，……………1分
……………3分
∴……………4分
(2)∵，
∴，……………6分
∴……………8分
19.（8分）（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AO＝CO，……………1分
∴∠PAO＝∠QCO，∠APO＝∠CQO……………3分
∴△APO≌△CQO，……………4分
∴OP＝OQ，……………5分
（2）四边形ODCQ的面积是3.6.……………8分
20.（8分）解：公路AB不需要暂时封锁．……………1分
理由如下：如图，过C作CD⊥AB于D．
∵CA⊥CB，
∴∠ACB＝90°，……………2分
∵BC＝1200米，AC＝500米，
∴根据勾股定理有AB＝（米）．……………3分
∵S△ABC＝AB•CD＝BC•AC……………5分
∴CD＝（米）．……………7分
由于400米＜米，故没有危险，……………8分
因此AB段公路不需要暂时封锁．……………8分
21.（8分）解：（1）射线OP即为所求，……………4分
（2）连结AB、EF交于点P，作射线OP，
∵四边形AEBF是平行四边形
∴AP＝BP，……………5分
又AO＝BO，OP＝OP，……………6分
∴△APO≌△BPO，……………7分
∴∠AOP＝∠BOP．……………8分
22.（10分）（1）证明：∵DE⊥AB，DF⊥AC
∴∠AED=∠F=90°……………1分
∵∠A=90°
∴四边形AEDF是矩形……………2分
∵∠CDF+∠EDE=∠CDE+∠BED=90°
∴∠CDF＝∠BDE……………3分
在△BDE和△CDF中
∴△BDE≌△CDF(AAS)，……………4分
∴DE=DF……………5分
∴四边形AEDF是正方形．……………6分
（2）解：∵∠A=90°，∠ABC=30°，AC=4
∴BC=2AC=8，AB=……………7分
设CF=BE=x
得
解得：……………9分
∴正方形AEDF的边长是．……………10分
23.（10分）解：（1）①由题意可知△ABC是直角三角形，
∵BC＝6，AB＝10，
∴AC=，
∴a＝AC﹣AA1＝8﹣1＝7，
∴B1C=，……………1分
∴b＝B1C﹣BC＝.……………2分
②当a＝b时，A1C＝8﹣a，CB1＝6+a，
由勾股定理得：A1C2+CB12＝A1B12，……………3分
即（8﹣a）2+（6+a）2＝102，
化简得a²-2a=0，
∵a＞0
∴a＝2．……………5分
(2)大，……………7分
25．……………10分
理由如下：以A1B1为底，过C作A1B1的垂线CD，D为垂足，取AB的中点O，
∴CD≤CO
在竹竿下滑过程中，当CD为△A1CB1的中线时，△A1CB1的面积最大，
最大值＝×10×5＝25．
24.（12分）解：（1）①③；……………4分
讲评：①设正方形的边长为，则对角线为，
∵，，
∴，
∴正方形不可能是闪亮四边形，①正确；
②设矩形的一组邻边为a、b，则对角线的平方为，
该矩形两边长乘积为，
∴若成立时，可满足闪亮四边形的定义，
∵，
∴恒成立，
∴矩形不可能是闪亮四边形，②错误；
③如图，在菱形ABCD中，AC为对角线，
若菱形ABCD为闪亮四边形，则AC2=AB·AD=AB2，
即：AC=AB，
∵AB=BC，
∴AB=AC=BC，△ABC为等边三角形，
∴∠BAC=60°，
∴∠BAD=120°，
∴若一个菱形是闪亮四边形，则必有一个角为120°，③正确；
（2）∵AD∥BC，∠ABC=90°，
∴∠BAD=90°，
∵AD=9，AB=12，
∴由勾股定理得BD2=225，……………5分
如图，作DE⊥BC于E点，则四边形ABED为矩形，
∴DE=AB=12，BE=AD=9，……………7分
在Rt△DEC中，CD=20，
由勾股定理得CE=16，
∴BC=BE+CE=25，……………8分
在Rt△ABC中，AC2=AB2+BC2=769，……………9分
∵AD·BC=9×25=225，……………10分
∴BD2=AD·BC，……………11分
∴四边形ABCD是闪亮四边形，BD为亮线．……………12分
25.（14分）（1）证明：①如图1，
∵点E，点F关于CD对称．
∴DE＝DF；CE＝CF，OE＝OF，CD⊥EF，…………1分
∴∠ECO＝∠FCO，
∵ED∥CF，
∴∠FCO＝∠EDO，…………2分
∴∠ECO＝∠EDO，
∴DE＝EC，
∴DE＝DE＝EC＝CF，
∴四边形ECFD是菱形．…………3分
②如图2，由得①得四边形ECFD是菱形，
∴OE＝OF＝EF，OD＝OC，……………4分
又∵AE＝EC，
∴OE＝AD……………5分
∴AD＝EF………………6分
（画图说明：∵CD⊥EF，OE为中位线，∴平行四边形ABCD是矩形）
（2）解：四边形ABCD是正方形，△BDF是直角三角形，则有以下情况：
Ⅰ．第一种情况：若∠BFD＝90°时，E、F、C三点重合，BF＝BE，即．………8分
Ⅱ．第二种情况：当∠BDF＝90°时，如图3，……………9分
∵四边形ABCD为正方形，
∴∠BDC＝45°，
∴∴∠CDF＝∠BDF-∠BDC=45°
∵点E与点F关于CD对称，
∴EF⊥CD，∠EDC＝∠CDF＝45°，
∵点E为AC上一点
∴E为AC与BD的交点，
∴BE＝DE，……………10分
∵DE=DF，
∴△EFD为等腰直角三角形，
∴DF＝DE＝BE，
在Rt△BDF中，BF＝，……………11分
∴即．……………12分
Ⅲ．点E为AC上一点，所以∠DBF＝90°不存在．……………13分
综上所述：若四边形ABCD是正方形，△BDF是直角三角形，的值为1或.………14分
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
B
A
D
C
A
C
B