2021-2022学年河北省石家庄市平山县八年级下学期期中数学试题及答案

这是一份2021-2022学年河北省石家庄市平山县八年级下学期期中数学试题及答案，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．式子在实数范围内有意义，则x的取值范围是（ ）
A．B．C．D．
2．下列说法中不正确的是（ ）
A．三个角度之比为3：4：5的三角形是直角三角形
B．三边之比为3：4：5的三角形是直角三角形
C．三个角度之比为1：2：3的三角形是直角三角形
D．三边之比为1：2：3的三角形是直角三角形
3．下列条件中，能确定一个四边形是平行四边形的是（ ）
A．一组对边相等B．一组对角相等
C．两条对角线相等D．两条对角线互相平分
4．下列说法正确的是（ ）
A．若，则B．若，则
С．D．5的平方根是
5．如图，一棵大树被大风刮断后，折断处离地面8m，树的顶端离树根6m，则这棵树在折断之前的高度是（ ）
A．18mB．10mC．14mD．24m
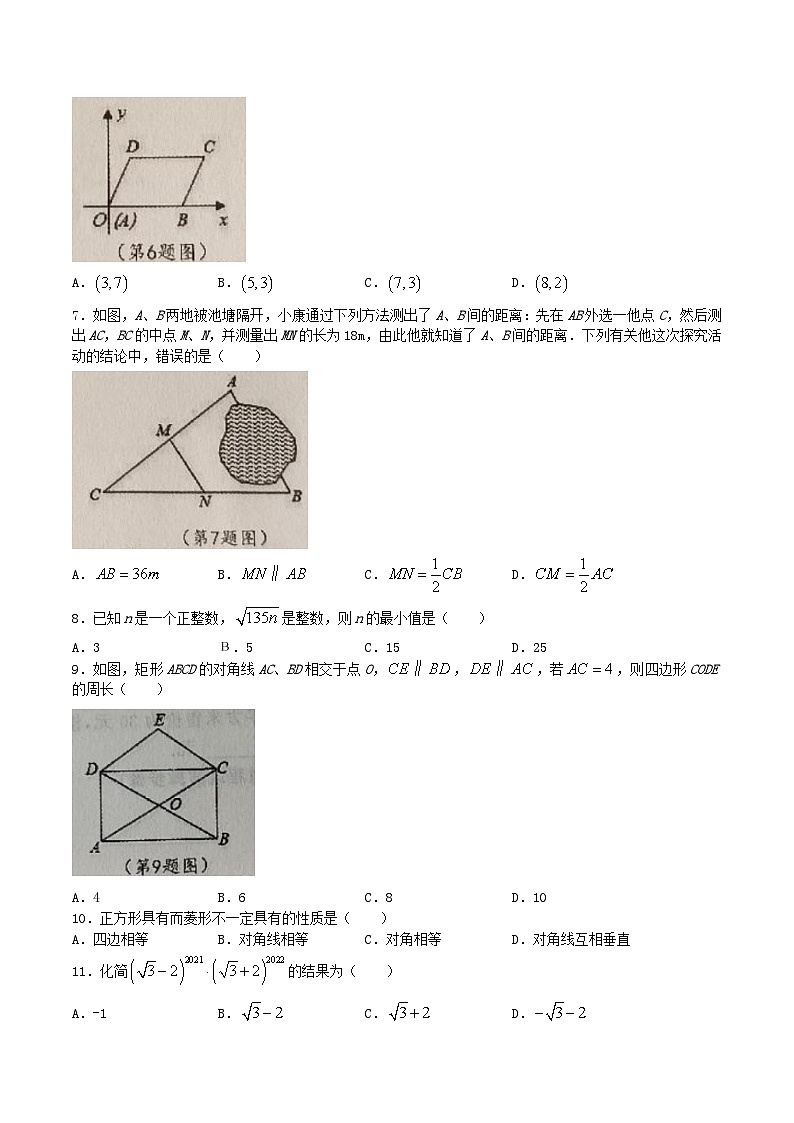
6．在平面直角坐标系中，平行四边形ABCD的顶点A，B，D的坐标分别是，，，则顶点C的坐标是（ ）
A．B．C．D．
7．如图，A、B两地被池塘隔开，小康通过下列方法测出了A、B间的距离：先在AB外选一他点C，然后测出AC，BC的中点M、N，并测量出MN的长为18m，由此他就知道了A、B间的距离．下列有关他这次探究活动的结论中，错误的是（ ）
A．B．C．D．
8．已知n是一个正整数，是整数，则n的最小值是（ ）
A．3В．5C．15D．25
9．如图，矩形ABCD的对角线AC、BD相交于点O，，，若，则四边形CODE的周长（ ）
A．4B．6C．8D．10
10．正方形具有而菱形不一定具有的性质是（ ）
A．四边相等B．对角线相等C．对角相等D．对角线互相垂直
11．化简的结果为（ ）
A．-1B．C．D．
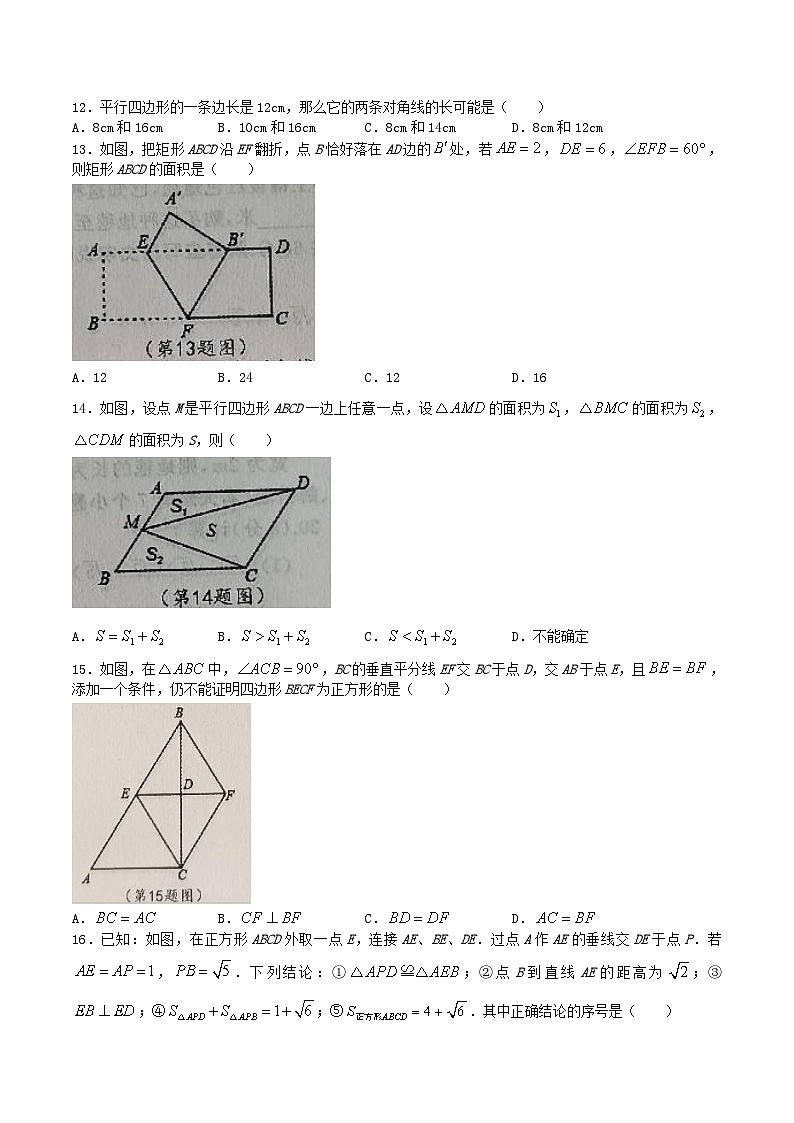
12．平行四边形的一条边长是12cm，那么它的两条对角线的长可能是（ ）
A．8cm和16cmB．10cm和16cmC．8cm和14cmD．8cm和12cm
13．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的处，若，，，则矩形ABCD的面积是（ ）
A．12B．24C．12D．16
14．如图，设点M是平行四边形ABCD一边上任意一点，设的面积为，的面积为，的面积为S，则（ ）
A．B．C．D．不能确定
15．如图，在中，，BC的垂直平分线EF交BC于点D，交AB于点E，且，添加一个条件，仍不能证明四边形BECF为正方形的是（ ）
A．B．C．D．
16．已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若，．下列结论：①；②点B到直线AE的距高为；③；④；⑤．其中正确结论的序号是（ ）
A．①③④B．①②⑤C．③④⑤D．①③⑤
二、填空题（本大题有3个小题，共10分，17~18小题各3分；19小题有两个空，每空2分）
17．一个三角形的三边长的比为3：4：5，且其周长为60cm，则其面积为______．
18．如图，正方形ABCD中，，若，则的度数是______．
19．某楼梯如图所示，欲在楼梯上铺设红色地毯，已知这种地毯每平方米售价为30元，楼梯宽为2m，则地毯的长为______米，购买这种地毯至少需要______元．
三、解答题（本大题有7个小题，共68分，解答应写出文字说明、证明过程或演算步骤）
20．（8分）计算：
（1）
（2）
21．（9分）
若，先化简再求的值．
22．（9分）
如图，在的方格纸中，每个小正方形的边长都为1，的三个顶点都在格点上，已知，，画出，并判断是不是直角三角形．
23．（9分）
杭州西湖风景游船处，如图，在离水面高度为5m的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13m，此人以0.5m/s的速度收绳．10s后船移动到点D的位置，问船向岸边移动了多少m？（假设绳子是直的，结果保留根号）
24．（10分）
如图，在四边形ABCD中，，，．
（1）求证：；
（2）若，，，求、的度数及四边形ABCD的周长．
25．（11分）
在中，于点D，点E为AC边的中点，过点A作，交DE的延长线于点F，连接CF．
（1）如图1，求证：四边形ADCF是矩形；
（2）如图2、当时，取AB的中点G，连接DG、EG，在不添加任何辅助线和字母的条件下，请直接写出图中所有的平行四边形（不包括矩形ADCF）．
26．（12分）
如图1，在矩形纸片ABCD中，，，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作交PQ于F，连接BF．
（1）求证：四边形BFEP为菱形；
（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；
①当点Q与点C重合时（如图2），求菱形BFEP的边长；
②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．
数学试卷答案
一、选择题（本大题共16个小题，共42分.1～10小题各3分，11～16小题各2分.在每小题给出的四个选项中，有且仅有一项是符合题目要求的）
1~5DADCA6~10CCCCB11~16DBDADD
二、填空题（本大题有3个小题，共10分.17～18小题各3分；19小题有两个空，每空2分）
17．；18．55°；19．7，420．
三、解答题（本大题有7个小题，共68分.解答应写出文字说明、证明过程或演算步骤）
20．（8分）计算：
解：（1）原式
；
（2）原式
．
21．（9分）
解：
．
∵，
∴原式．
把代入得：
．
22．（9分）
解：如图，即为所求．
∵，，
∴，
∵，
∴，
∴是直角三角形．
23．（9分）
解：∵在中，，，，
∴（m），
∵此人以0.5m/s的速度收绳，10s后船移动到点D的位置，
∴（m），
∴（m），
∴（m）．
答：船向岸边移动了m．
24．（10分）
（1）证明：∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，∴AB＝CD．
又∵AN＝CM，∴，即BN＝DM；
（2）∵AB∥CD，∴，
∵，∴．
由（1）知，四边形ABCD是平行四边形，
∴，，．
∵，，
∴四边形ABCD的周长．
25．（11分）
（1）证明：∵AF∥BC，∴，
∵E是AC中点，∴，在△AEF和△CED中，
，∴△AEF≌△CED，
∴，∵，
∴四边形ADCF是平行四边形，
∵，∴，
∴四边形ADCF是矩形．
（2）∵线段DG、线段GE、线段DE都是△ABC的中位线，又AF∥BC，
∴AB∥DE，DG∥AC，EG∥BC，
∴四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形．
26．（12分）
（1）证明：∵折叠纸片使B点落在边AD上的E处，折痕为PQ，
∴点B与点E关于PQ对称，∴，，，
又∵EF∥AB，∴∠BPF＝∠EFP，∴∠EPF＝∠EFP，∴EP＝EF，
∴，∴四边形BFEP为菱形；
（2）解：①∵四边形ABCD是矩形，
∴，，∠A＝∠D＝90°，
∵点B与点E关于PQ对称，∴，
在Rt△CDE中，，
∴；
在Rt△APE中，AE＝1，，
∴，
解得：EP＝5/3cm，
∴菱形BFEP的边长为5/3cm；
②当点Q与点C重合时，如图2，点E离点A最近，由①知，此时AE＝1cm；
当点P与点A重合时，如图3，点E离点A最远，此时四边形ABQE为正方形，AE＝AB＝3cm，
∴点E在边AD上移动的最大距离为2cm．