安徽省合肥市包河区2024年中考数学三模试卷附答案

这是一份安徽省合肥市包河区2024年中考数学三模试卷附答案，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1． 在、、、这四个数中，最小的数是（ ）
A．B．C．D．
2． 近年来，我国水利部大力实施农村供水工程建设，累计完成了农村供水工程投资亿元，解决了亿农村居民的饮水安全问题，数据亿用科学记数法表示为（ ）
A．B．C．D．
3． 以下计算正确的是（ ）
A．B．
C．D．
4．如图所示的几何体的俯视图是（ ）
A．B．C．D．
5． 五名同学在“爱心捐助”活动中，捐款数额如下单位：元：，，，，，这组数据的中位数和众数分别是（ ）
A．和B．和C．和D．和
6． 某校开展“劳动创造美好幸福生活”演讲比赛，有位女同学和位男同学获得一等奖，要从这位同学中随机抽取一男一女两位同学做获奖感言，女同学陶梦和男同学张军恰好来自同一班级，则他俩同时被抽中的概率为（ ）
A．B．C．D．
7． 某景区统计年元月到月的游客人数，发现月份的游客人数是元月份的倍设、月份游客人数的平均增长率为，则下列方程正确的是（ ）
A．B．
C．D．
8． 若，，则的值为（ ）
A．B．C．D．
9．已知：中，为边中点，过点的直线交延长线于，交于，记，，则（ ）
A．B．C．D．
10．已知二次函数的最大值为，若，则下列结论错误的是（ ）
A．，B．
C．D．
二、填空题（本大题共4小题，共20.0分）
11． 计算 ．
12． 分解因式： ．
13． 如图，直线与半径为的相切于点，点在上，连接、，且，弦，则的长为 ．
14． 在中，，，，是边的中点，点在边上，将沿直线翻折，使得点落在同一平面内的点处请完成下列问题：
① ；
②当时，的长为 ．
三、解答题（本大题共9小题，共90.0分。解答应写出文字说明，证明过程或演算步骤）
15．解不等式：．
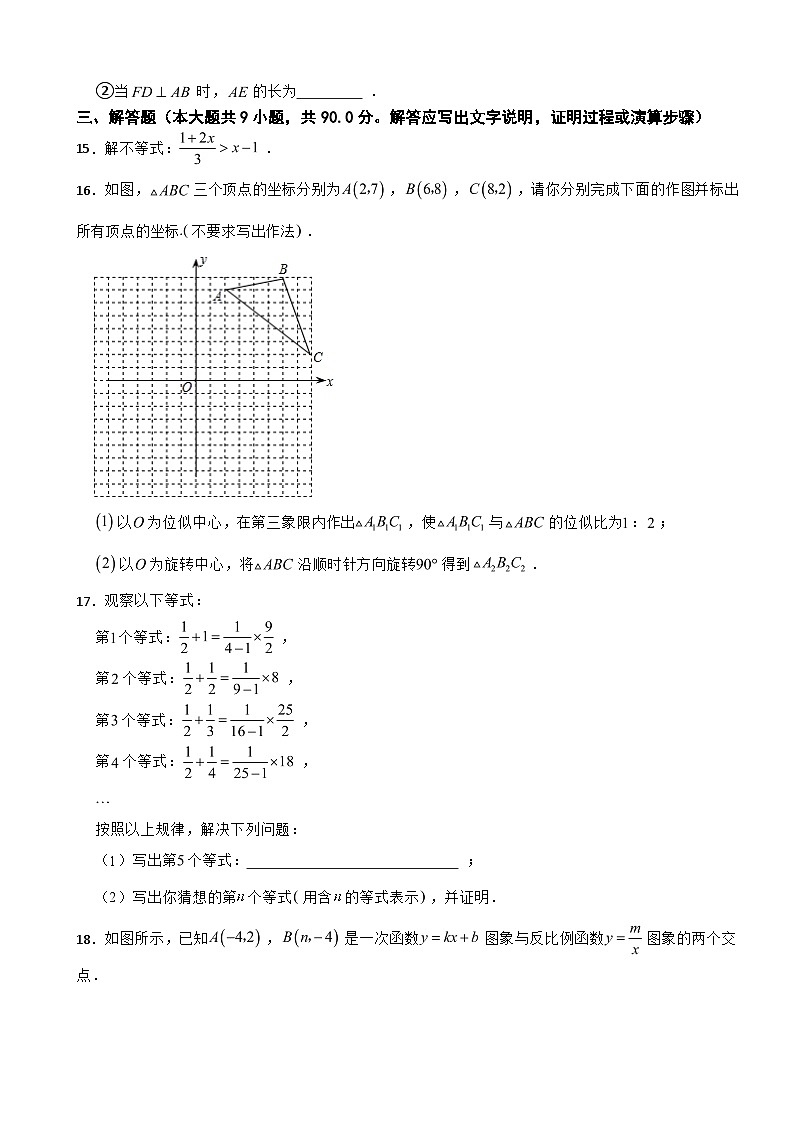
16．如图，三个顶点的坐标分别为，，，请你分别完成下面的作图并标出所有顶点的坐标不要求写出作法．
以为位似中心，在第三象限内作出，使与的位似比为：；
以为旋转中心，将沿顺时针方向旋转得到．
17．观察以下等式：
第个等式：，
第个等式：，
第个等式：，
第个等式：，
按照以上规律，解决下列问题：
（1）写出第个等式： ；
（2）写出你猜想的第个等式用含的等式表示，并证明．
18．如图所示，已知，是一次函数图象与反比例函数图象的两个交点．
（1）求反比例函数和一次函数的表达式；
（2）观察图象，当取何值时，．
19．如图，在一个坡度或坡比：的山坡上发现有一棵古树测得古树底端到山脚点的距离米，在距山脚点水平距离米的点处，测得古树顶端的仰角古树与山坡的截面、点在同一平面上，古树与直线垂直，求古树的高度参考数据：，，
20．已知：如图，四边形是的内接四边形，直径交边于点，、的延长线相交于点连接，若．
（1）求证：；
（2）若，，求半径．
21．每年春天，茶叶庄园利用机器人进行茶叶采摘工作，然后按照叶片长度分类加工制成茶叶，为了解甲、乙两款机器人采摘茶叶的质量，分别随机抽取了茶叶做检测，获得了它们的茶叶长度单位：，并对样本数据茶叶长度进行了整理、描述和分析下面给出了部分信息．
茶叶长度对应的茶叶等级如下：
说明：等级是一等品，二等品为优质茶叶其中等级是一等品为精品茶叶；等级是三等品的为一般茶叶．
甲款机器人采摘茶叶的样本数据的频数分布统计表如下不完整：
乙款机器人采摘茶叶的样本数据的频数分布直方图如下：
甲款机器人样本数据的频数分布表
两款机器人采摘的茶叶样本数据的平均数、中位数、众数、方差如下：
根据以上信息，回答下列问题：
（1）的值为 ，的值为 ．
（2）若甲款机器人采摘茶叶，其中优质茶叶约有 ，若乙款机器人采摘茶叶共，估计精品茶叶有 ：
（3）根据图表数据，你认为哪款机器人采摘茶叶的质量较好，并说明理由从某个角度说明推断的合理性
22．已知抛物线交轴于，两点，其中点的坐标为，对称轴为点，为坐标平面内两点，其坐标为，．
（1）求抛物线的解析式及顶点坐标；
（2）连接，若抛物线向下平移个单位时，与线段只有一个公共点，求的取值范围．
23．已知：菱形中，，，与交于点，点为上一点．
（1）求的长；
（2）若，求证：；
（3）若点在线段上不与、重合，以为对称轴，折叠，使点的对应点恰好落在菱形的边上，画出图形并求的长．
1．C
2．A
3．C
4．C
5．B
6．D
7．C
8．B
9．A
10．D
11．
12．
13．
14．10；8
15．解：，
，
，
，
．
16．解：如图：
如图.
17．（1）解：；
（2）解：，
左边，
右边，
左边右边．
18．（1）解：把代入得：，
则反比例函数的解析式是：；
把代入，得：，
则的坐标是．
根据题意得：，
解得：，
则一次函数的解析式是：；
（2）解：观察图象，当或时，．
19．解：如图，设与交于，
，
设，，
，
，
，，
，
，
，
，
，
，
答：古树的高度约为米．
20．（1）证明：连接，
与是同弦所对圆周角，
，
，
，
为的直径，为圆周上一点，
，
，
，
，即；
（2）解：四边形是的内接四边形，
，
，
，
连接，由垂径定理得，
，
在中，，
设半径为，则有，
解得，，
半径为．
21．（1）10；0.64
（2）480；350
（3）解：我认为甲款机器人采摘茶叶的质量较好，理由如下：
理由：甲款机器人采摘茶叶的质量的极差和方差都小于乙款机器人，产品的稳定性更好．答案不唯一．
22．（1）解：抛物线对称轴为直线，
，
，
将点的坐标代入，解得，
，
抛物线的顶点为．
（2）解：抛物线平移后的解析式为，
平移后的顶点坐标为，
当抛物线顶点落在上时，，解得，
当抛物线经过时，，解得，
当抛物线经过点，，解得，
时，满足题意．
综上所述，或．
23．（1）解：四边形是菱形，，，，
，
；
（2）证明：，，
，，
，，
，
∽，
，即，
，
，
．
（3）解：如图，当点在边上时，延长交于点，
由折叠知，则，
由可知，
如图，当点落在边上时，
由折叠可知，
，
，，
，
，
∽，
，
，
．
的长为或．茶叶长度
等级
三等品
二等品
一等品
二等品
三等品
分组
频数
频率


合计
平均数
中位数
众数
方差
甲机器人
乙机器人