第11讲 导数与函数的极值、最值-【寒假讲义】高二数学寒假讲义练习（人教B版 选择性必修三）

这是一份第11讲 导数与函数的极值、最值-【寒假讲义】高二数学寒假讲义练习（人教B版 选择性必修三），文件包含第11讲导数与函数的极值最值教师卷-寒假衔接讲义高二数学寒假讲义练习人教B用选择性必修三docx、第11讲导数与函数的极值最值学生卷-寒假衔接讲义高二数学寒假讲义练习人教B用选择性必修三docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

1.借助函数图像，了解函数在某点取得极值的必要和充分条件.
2.会用导数求函数的极大值、极小值.
3.会求闭区间上函数的最大值、最小值.
【知识导航】
1.函数的极值
一般地，设函数f(x)在x0处可导，且f′(x0)＝0.
(1)如果对于x0左侧附近的任意x，都有_______；对于x0右侧附近的任意x，都有_______，那么此时x0是f(x)的极大值点.
(2)如果对于x0左侧附近的任意x，都有_______；对于x0右侧附近的任意x，都有_______，那么此时x0是f(x)的极小值点.
(3)如果f′(x)在x0的左侧附近与右侧附近均为正号(或均为负号)，则x0一定不是y＝f(x)的极值点.
(4)极小值点、极大值点统称为_______，极小值和极大值统称为_______.
2.函数的最大(小)值
(1)函数f(x)在[a，b]上的最值
如果函数y＝f(x)的定义域为[a，b]且存在最值，函数y＝f(x)在(a，b)内可导，那么函数的最值点要么是区间端点a或b，要么是极值点.
(2)求y＝f(x)在区间[a，b]上的最大(小)值的步骤：
①求函数y＝f(x)在区间(a，b)上的_______；
②将函数y＝f(x)的各极值与端点处的函数值_______比较，其中最大的一个是最大值，最小的一个是最小值.
1.求最值时，应注意极值点和所给区间的关系，关系不确定时，需要分类讨论，不可想当然认为极值就是最值.
2.函数最值是“整体”概念，而函数极值是“局部”概念，极大值与极小值之间没有必然的大小关系.
【知识预习】
考点一：由导数求函数的极值和最值
1．函数有（ ）
A．极大值为5，无极小值B．极小值为，无极大值
C．极大值为5，极小值为D．极大值为5，极小值为
2．已知函数，则（ ）
A．函数的极大值为，无极小值B．函数的极小值为，无极大值
C．函数的极大值点为，无极小值点D．函数的极小值点为，无极大值点
3．已知函数，则下列说法正确的是（ ）
A．的极小值为B．的极大值为
C．在区间上单调递增D．在区间上单调递减
4．函数的极大值为（ ）
A．2B．C．10D．
5．关于函数极值的判断，正确的是（ ）
A．x＝1时，y极大值＝0
B．x＝e时，y极大值＝
C．x＝e时，y极小值＝
D．时，y极大值＝
考点二：函数图像与极值、最值关系
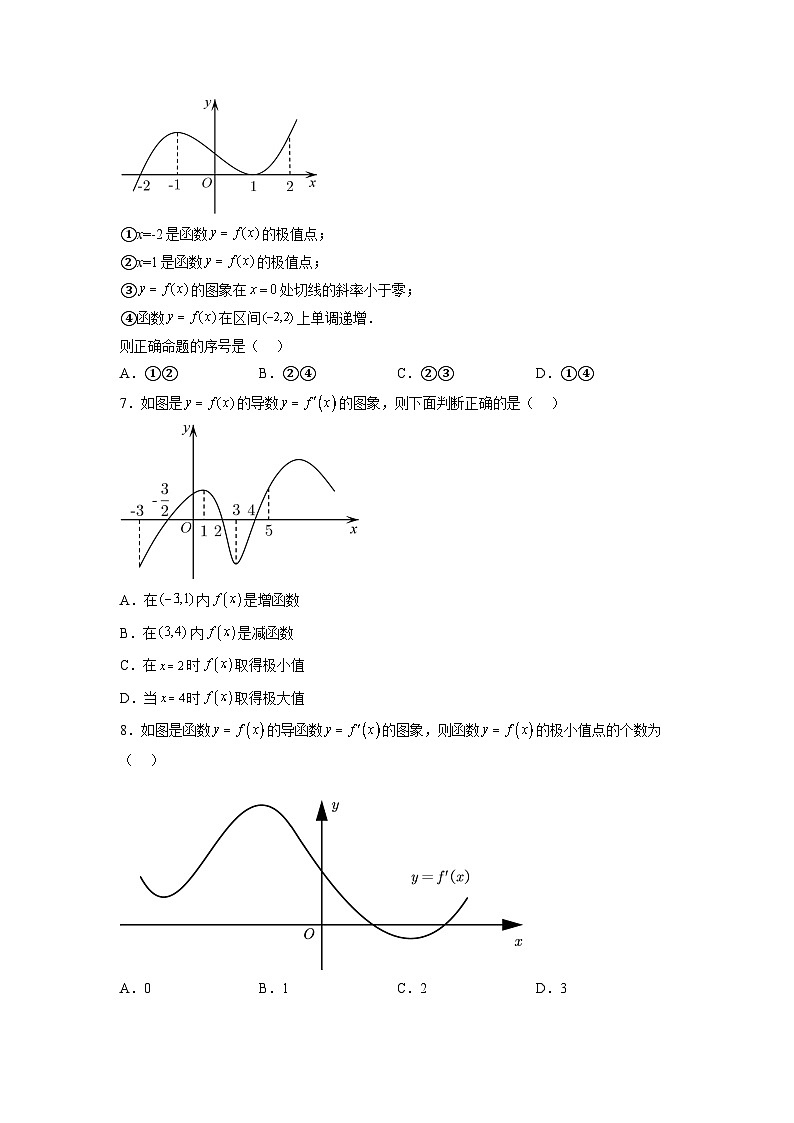
6．如图是函数的导函数的图象，给出下列命题：
①x=-2是函数的极值点；
②x=1是函数的极值点；
③的图象在处切线的斜率小于零；
④函数在区间上单调递增．
则正确命题的序号是（ ）
A．①②B．②④C．②③D．①④
7．如图是的导数的图象，则下面判断正确的是（ ）
A．在内是增函数
B．在内是减函数
C．在时取得极小值
D．当时取得极大值
8．如图是函数的导函数的图象，则函数的极小值点的个数为（ ）
A．0B．1C．2D．3
9．已知函数的导函数的图象如图所示，则下列结论正确的是（ ）
A．函数在上是增函数
B．是函数的极小值点
C．
D．
10．已知函数的导函数的图象如图所示，那么（ ）
A．函数在上不单调
B．函数在的切线的斜率为0
C．是函数的极小值点
D．是函数的极大值点
考点三：极值、最值含参问题的讨论
11．已知函数的最小值为－1，则实数a＝（ ）
A．－1B．0C．1D．2
12．若函数在上的最小值为，则a的值为（ ）
A．0B．1C．D．
13．若函数有最小值，则实数的取值范围为（ ）
A．B．C．D．
14．已知函数在区间上有最小值，则实数的取值范围是（ ）
A．B．
C．D．
15．函数在区间上有最大值，则m的取值范围是（ ）
A．B．
C．D．
【对点训练】
一、单选题
1．已知函数的导函数则的极值点的个数为（ ）
A．0B．1C．2D．3
2．若函数在处有极值，则（ ）
A．B．
C．D．a不存在
3．已知是函数的导函数，函数的图象如图所示，则的极大值点为（ ）
A．B．C．D．
4．若是函数的极值点，则的值是（ ）
A．B．0C．1D．
5．某箱子的体积V与底面边长x的关系为，则当箱子的体积最大时，箱子的底面边长为（ ）
A．30B．40C．50D．55
6．已知函数，则（ ）
A．函数的极大值为，无极小值B．函数的极小值为，无极大值
C．函数的极大值为0，无极小值D．函数的极小值为0，无极大值
7．若对任意的 ，，且，都有，则m的最小值是（ ）
A．B． C．1D．
8．函数的图像如图所示，则关于函数的说法正确的是（ ）
A．函数有3个极值点
B．函数在区间上是增加的
C．函数在区间上是增加的
D．当时，函数取得极大值
二、多选题
9．已知函数，则（ ）
A．有两个极值点B．直线是曲线的切线
C．有一个零点D．过点与曲线相切的直线有且只有1条
10．已知函数，则（ ）
A．恒成立B．是上的减函数
C．在得到极大值D．在区间内只有一个零点
三、填空题
11．函数的极大值与极小值分别为和，则____．
12．函数的导函数的图像如图所示，给出下列命题：
①是函数的极值点；
②是函数的最小值点；
③在区间上严格增；
④在处切线的斜率小于零.
以上正确命题的序号是______.
四、解答题
13．已知函数在处取得极值.
(1)求实数的值；
(2)求函数在上的最大值和最小值.
14．已知函数.
(1)当时，求函数在上的最大值和最小值；
(2)若函数在区间内存在极小值，求实数的取值范围.
15．已知．
(1)若有最值，求实数a的取值范围；
(2)若当时，，求实数a的取值范围．
【提升作业】
一、单选题
1．已知函数有两个极值点，则实数的取值范围是（ ）
A．B．
C．D．
2．已知，函数的导函数为.下列说法正确的是（ ）
A．B．函数的严格增区间为
C．的极大值为D．方程有两个不同的解
3．已知函数在区间恰有3个极值点，2个零点，则的取值范围是（ ）
A．B．C．D．
4．已知函数的导函数的图象如图所示，则下列关于函数的表述，不正确的是（ ）
A．在上为减函数B．在上为增函数
C．在处取极小值D．在处取极小值
5．已知函数，则下列结论正确的为（ ）
A．是的极小值点B．是的极大值点
C．的最小值为D．的最大值为3
二、填空题
6．已知函数存在极值点，则实数a的取值范围是_____________．
7．若不等式（其中是自然对数的底数）对恒成立，则实数的取值范围为________
三、解答题
8．求函数．
(1)求函数的单调区间和极值；
(2)求在区间上的最值．
9．已知函数．
(1)证明：当a＝1时，；
(2)若是f（x）的极小值点，求a的取值范围．
10．已知函数．
(1)求曲线在点处的切线方程；
(2)求函数的最小值；
(3)求函数的零点个数，并说明理由．