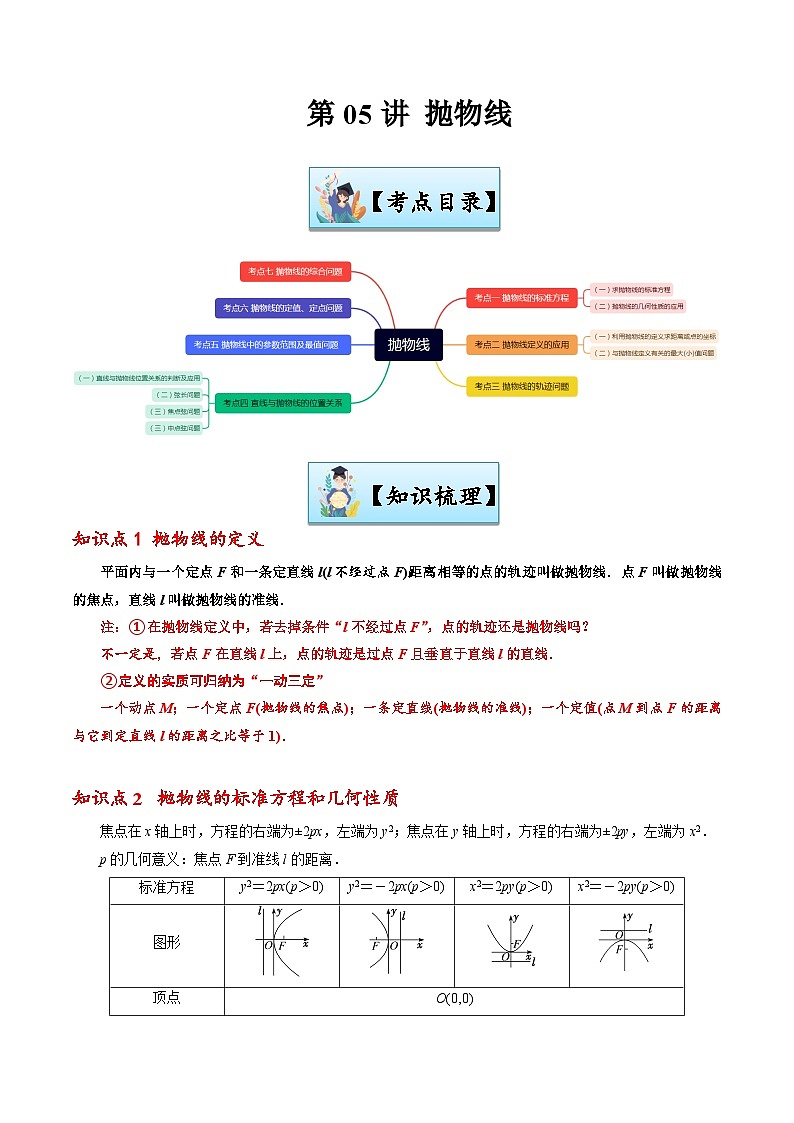
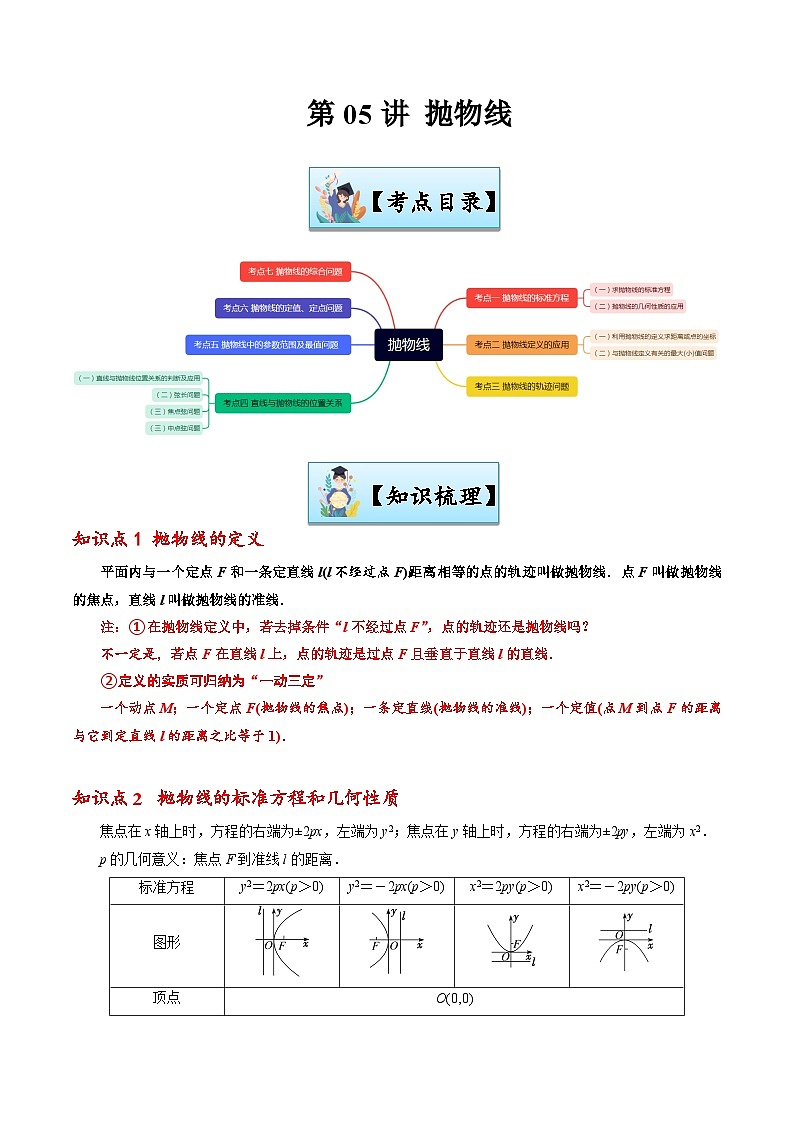
第05讲 抛物线-【寒假讲义】高二数学寒假讲义练习（新人教A专用）

这是一份第05讲 抛物线-【寒假讲义】高二数学寒假讲义练习（新人教A专用），文件包含第05讲抛物线-寒假衔接讲义高二数学寒假讲义练习新人教A专用教师卷docx、第05讲抛物线-寒假衔接讲义高二数学寒假讲义练习新人教A专用学生卷docx等2份试卷配套教学资源，其中试卷共73页， 欢迎下载使用。


【知识梳理】
知识点1 抛物线的定义
平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．
注：①在抛物线定义中，若去掉条件“l不经过点F”，点的轨迹还是抛物线吗？
不一定是，若点F在直线l上，点的轨迹是过点F且垂直于直线l的直线．
②定义的实质可归纳为“一动三定”
一个动点M；一个定点F(抛物线的焦点)；一条定直线(抛物线的准线)；一个定值(点M到点F的距离与它到定直线l的距离之比等于1)．
知识点2 抛物线的标准方程和几何性质
焦点在x轴上时，方程的右端为±2px，左端为y2；焦点在y轴上时，方程的右端为±2py，左端为x2．
p的几何意义：焦点F到准线l的距离．
知识点3 直线与抛物线的位置关系
设直线l：y＝kx＋m，抛物线：y2＝2px(p>0)，将直线方程与抛物线方程联立整理成关于x的方程k2x2＋2(km－p)x＋m2＝0.
(1)若k≠0，当Δ>0时，直线与抛物线相交，有两个交点；
当Δ＝0时，直线与抛物线相切，有一个交点；
当Δ<0时，直线与抛物线相离，没有公共点．
(2)若k＝0，直线与抛物线有一个交点，此时直线平行于抛物线的对称轴或与对称轴重合．
注：(1)直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件．
(2)研究直线与抛物线的关系时要注意直线斜率不存在的情况．
知识点4 弦长问题
过抛物线y2＝2px(p>0)的焦点的直线交抛物线于A(x1，y1)，B(x2，y2)两点，那么线段AB叫做焦点弦，
如图：设AB是过抛物线y2＝2px(p>0)焦点F的弦，若A(x1，y1)，B(x2，y2)，则|AB|＝x1＋x2＋p.
注：(1)x1·x2＝eq \f(p2,4).
(2)y1·y2＝－p2.
(3)|AB|＝x1＋x2＋p＝eq \f(2p,sin2α) (α是直线AB的倾斜角)．
(4)eq \f(1,|AF|)＋eq \f(1,|BF|)＝eq \f(2,p)为定值(F是抛物线的焦点)．
（5）求弦长问题的方法
①一般弦长：|AB|＝eq \r(1＋k2)|x1－x2|，或|AB|＝eq \r(1＋\f(1,k2))|y1－y2|.
②焦点弦长：设过焦点的弦的端点为A(x1，y1)，B(x2，y2)，则|AB|＝x1＋x2＋p.
【考点剖析】
考点一 抛物线的标准方程
求抛物线的标准方程
1．（2023春·北京海淀·高二校考阶段练习）抛物线的焦点在轴正半轴上，且准线与焦点轴间的距离为3，则此抛物线的标准方程为（ ）
A．B．C．D．
2．（2023春·辽宁本溪·高二校考阶段练习）以坐标轴为对称轴，焦点在直线上的抛物线的标准方程为（ ）
A．或B．或
C．或D．或
3．（2023秋·上海黄浦·高二上海市向明中学校考期末）过点，且焦点在y轴上的抛物线的标准方程是（ ）
A．B．C．D．
（二）抛物线的几何性质的应用
4．（2023·全国·高二假期作业）抛物线的准线方程为（ ）
A．B．
C．D．
5．（2023春·山东临沂·高二临沂第四中学校考阶段练习）若抛物线的焦点与双曲线的右焦点重合，则（ ）
A．2B．4C．D．
6．（2023春·黑龙江哈尔滨·高二哈九中校考阶段练习）已知圆与抛物线的准线相切，则（ ）
A．B．C．8D．2
7．（2023·全国·高二假期作业）已知抛物线，则抛物线的焦点坐标为（ ）
A．B．C．D．
8．（2023春·江苏泰州·高二统考期中）若抛物线上一点到其焦点的距离等于4，则（ ）
A．B．C．D．
9．（2023秋·湖北咸宁·高二统考期末）已知O是坐标原点，F是抛物线C：的焦点，是C上一点，且，则的面积为（ ）
A．8B．6C．4D．2
考点二 抛物线定义的应用
（一）利用抛物线的定义求距离或点的坐标
10．（2023秋·新疆乌鲁木齐·高二乌市八中校考期末）抛物线上一点到其焦点的距离为，则点到坐标原点的距离为（ ）
A．B．C．D．2
11．（2023·高二单元测试）已知曲线C上任意一点P到定点的距离比点P到直线的距离小1，M，N是曲线C上不同的两点，若，则线段MN的中点Q到y轴的距离为（ ）
A．3B．4C．5D．6
12．（2023·高二课时练习）若是抛物线上一点，为抛物线的焦点，则（ ）．
A．B．C．D．
13．（2023·高二课时练习）已知抛物线C：的焦点为F，是C上一点，，则（ ）
A．1B．2C．4D．5
14．（2023秋·新疆喀什·高二新疆维吾尔自治区喀什第二中学校考期中）已知A，F为抛物线的焦点，点M在抛物线上移动，当取最小值时，点的坐标为（ ）
A．B．C．D．
15．（2023春·湖北武汉·高二华中师大一附中阶段练习）已知抛物线的焦点为F，点M在抛物线C的准线l上，线段与y轴交于点A，与抛物线C交于点B，若，则（ ）
A．1B．2C．3D．4
16．（2023春·福建·高二福建师大附中校考期末）如图，过抛物线的焦点F的直线l交抛物线于点A，B，交其准线于点C，准线与对称轴交于点M，若，且，则p为（ ）
A．1B．2C．3D．4
（二）与抛物线定义有关的最大(小)值问题
17．（2023·高二单元测试）已知圆C经过点，且与直线相切，则其圆心到直线距离的最小值为（ ）
A．3B．2C．D．
18．（2023春·四川泸州·高二四川省泸县第一中学校考期末）已知抛物线：的焦点为，抛物线上有一动点，，则的最小值为（ ）
A．5B．6C．7D．8
19．（2023秋·江西赣州·高二校联考期中）已知抛物线的焦点为F，P点在抛物线上，Q点在圆上，则的最小值为（ ）
A．4B．6C．8D．10
20．（2023春·黑龙江哈尔滨·高二哈尔滨三中校考期中）设点P是抛物线:上的动点,点M是圆:上的动点,d是点P到直线的距离,则的最小值是（ ）
A．B．C．D．
21．（2023春·北京·高二人大附中校考期末）已知直线和直线，则抛物线上一动点到直线和直线的距离之和的最小值是（ ）
A．B．C．2D．
考点三 抛物线的轨迹问题
22．（2023·高二课时练习）已知点，直线，若动点到的距离等于，则点的轨迹是（ ）
A．椭圆B．双曲线
C．抛物线D．直线
23．（2023春·四川成都·高二成都七中校考阶段练习）已知圆，点，动圆经过点A且与圆O相切，记动圆圆心M的轨迹为E，有下列几个命题：
①，则轨迹E表示圆，②，则轨迹E表示椭圆，③，则轨迹E表示抛物线，④，则轨迹E表示双曲线，其中，真命题的个数为（ ）
A．B．C．D．
24．（2023秋·福建福州·高二统考期中）在平面直角坐标系xOy中，动点到直线的距离比它到定点的距离小1，则P的轨迹方程为（ ）
A．B．
C．D．
25．（2023春·广东江门·高二新会陈经纶中学校考阶段练习）已知点，过直线上一动点P作与y轴垂直的直线，与线段的中垂线交于点Q，则Q点的轨迹方程为（ ）
A．B．C．D．
26．（2023秋·山东青岛·高二青岛二中校考阶段练习）已知动圆M与直线y=2相切，且与定圆 外切，则动圆圆心M的轨迹方程为（ ）
A． B．C． D．
27．（2023·高二课时练习）若动点满足，则点M的轨迹是（ ）
A．圆B．椭圆C．双曲线D．抛物线
考点四 直线与抛物线的位置关系
直线与抛物线位置关系的判断及应用
28．（2023春·上海浦东新·高二上海市建平中学校考阶段练习）过定点且与抛物线有且仅有一个公共点的直线有（ ）
A．1条B．2条C．3条D．4条
29．（2023·高二课时练习）直线与抛物线的位置关系为（ ）
A．相交B．相切C．相离D．不能确定
30．（2023春·江苏连云港·高二期末）已知直线l过点且与抛物线只有一个公共点，则直线l的方程是（ ）
A．B．
C．D．或
31．（2023春·江苏南京·高二校联考阶段练习）过抛物线的焦点作直线交抛物线于两点，且点在第一象限，则当时，直线的斜率为（ ）
A．B．C．D．
32．（2023春·江苏连云港·高二校考期中）过抛物线上定点作圆的两条切线，分别交抛物线于另外两点、，则直线的方程为（ ）
A．B．
C．D．
33．（2023秋·安徽·高二校联考期末）已知抛物线的焦点为，其准线与轴的交点为，点为抛物线上一动点，当取得最大值时，直线的倾斜角为（ ）
A．B．C．或D．或
弦长问题
34．（2023春·四川成都·高二树德中学校考阶段练习）已知抛物线的焦点为，过点且倾斜角为的直线与抛物线交于，两点，则（ ）．
A．8B．C．16D．32
35．（2023春·湖北·高二校联考阶段练习）根据抛物线的光学性质，从抛物线的焦点发出的光，经抛物线反射后光线都平行于抛物线的轴，已知抛物线，若从点发射平行于轴的光射向抛物线的A点，经A点反射后交抛物线于点，则（ ）
A．B．C．D．
36．（2023春·山东济南·高二山东省济南市莱芜第一中学校考阶段练习）已知椭圆的右焦点是抛物线的焦点，则过作倾斜角为45°的直线分别交抛物线于，（在轴上方）两点，则的值为（ ）
A．B．C．3D．4
37．（2023·山东青岛·高二山东省莱西市第一中学学业考试）设F为抛物线的焦点，过F且倾斜角为30°的直线交抛物线C于A，B两点，O为坐标原点，则的面积为（ ）
A．B．C．D．
38．（2023春·河南·高二校联考期中）已知抛物线的焦点为为上一点，且在第一象限，直线与的准线交于点，过点且与轴平行的直线与交于点，若，则的面积为（ ）
A．8B．12C．D．
39．（2023秋·河南许昌·高二统考期末）已知直线l过点，且垂直于x轴．若l被抛物线截得的线段长为，则抛物线的焦点坐标为（ ）
A．B．C．D．
40．（2023秋·河南·高二校联考开学考试）已知A，B为抛物线，上的两点，且，则AB的中点横坐标的最小值为（ ）．
A．B．C．D．1
41．（2023秋·广东深圳·高二深圳市罗湖外语学校校考阶段练习）已知圆与抛物线相交于M，N，且，则（ ）
A．B．2C．D．4
焦点弦问题
42．（2023春·湖南长沙·高二湘府中学校考阶段练习）设F为抛物线的焦点，点M在C上，点N在准线l上，满足，，则（ ）
A．B．C．2D．
43．（2023·全国·高二假期作业）已知抛物线的焦点为F，N为C上一点，且N在第一象限，直线与C的准线交于点M，过点M且与x轴平行的直线与C交于点P，若，则直线的斜率为（ ）
A．1B．2C．D．
44．（2023春·四川绵阳·高二四川省绵阳南山中学校考期中）已知直线过抛物线的焦点F，且与抛物线交于A，B两点，与抛物线的准线交于C点，若，则等于（ ）
A．2B．3C．D．
45．（2023春·浙江金华·高二浙江金华第一中学校考阶段练习）设倾斜角为α的直线l经过抛物线C：的焦点F，与抛物线C交于A、B两点，设A在x轴上方，点B在x轴下方．若，则的值为（ ）
A．B．C．D．
（四）中点弦问题
46．（2023春·湖北省直辖县级单位·高二校考期中）若抛物线的弦AB中点坐标为，则直线AB的斜率为（ ）
A．－4B．4C．－2D．2
47．（2023春·江西·高二校联考期中）已知抛物线，过点的直线与抛物线交于两点.若，则直线的斜率是（ ）
A．3B．C．D．
48．（2023·高二单元测试）在平面直角坐标系xOy中，已知抛物线的焦点为F，若A、B为抛物线上两点，且线段AB的垂直平分线交x轴于点M．当，时，抛物线的方程为（ ）．
A．B．C．D．
49．（2023春·四川成都·高二校考阶段练习）已知抛物线，过其焦点且斜率为1的直线交抛物线于A，B两点，若线段AB的中点的横坐标为3，则该抛物线的准线方程为（ ）
A．B．C．D．
考点五 抛物线中的参数范围及最值问题
50．（2023春·安徽宿州·高二校联考期末）抛物线上一点到直线距离的最小值为（ ）
A．B．C．D．
51．（2023·高二单元测试）已知点P在抛物线上，点Q在圆上，则的最小值为（ ）
A．B．C．D．
52．（2023·高二单元测试）已知点（x，y）在抛物线y2=4x上，则的最小值是（ ）
A．2B．3C．4D．0
53．（2023·高二单元测试）已知过点的直线与抛物线相交于，两点，点，若直线，的斜率分别为，，则的取值范围是（ ）
A．B．
C．D．
考点六 抛物线的定值、定点问题
54．（2023春·陕西渭南·高二统考期末）已知抛物线的焦点为，点在抛物线上，且．
(1)求抛物线的方程；
(2)过点且斜率存在的直线交抛物线于不同的两点，设为坐标原点，直线的斜率分别为，求证：为定值．
55．（2023·全国·高二假期作业）已知点在抛物线上，且到的焦点的距离与到轴的距离之差为.
(1)求的方程；
(2)当时，是上不同于点的两个动点，且直线的斜率之积为为垂足.证明：存在定点，使得为定值.
56．（2023春·黑龙江·高二黑龙江实验中学校考期中）已知抛物线：上一点到焦点的距离为，
(1)求抛物线的方程；
(2)若在第一象限，不过的直线与抛物线相交于，两点，且直线，的斜率之积为，证明：直线过定点．
57．（2023·全国·高二假期作业）已知抛物线的焦点到准线的距离为1．
(1)求抛物线的标准方程；
(2)设点是该抛物线上一定点，过点作圆（其中）的两条切线分别交抛物线于点，连接．探究：直线是否过一定点，若过，求出该定点坐标；若不经过定点，请说明理由．
考点七 抛物线的综合问题
58．【多选】（2023春·江西上饶·高二校联考阶段练习）已知抛物线C:的焦点，过的直线交抛物线于A，B两点，O为坐标原点，则以下说法正确的是（ ）
A．为定值B．AB中点的轨迹方程为
C．最小值为16D．O在以AB为直径的圆外
59．【多选】（2023·全国·高二假期作业）已知抛物线：的焦点为F，准线为，过点F的直线与抛物线交于，两点，点在上的射影为，则下列说法正确的是（ ）
A．若，则
B．以为直径的圆与准线相切
C．设，则
D．过点与抛物线C有且仅有一个公共点的直线至多有2条
60．【多选】（2023春·浙江·高二慈溪中学校联考阶段练习）已知为坐标原点，过抛物线的焦点的直线交于两点，则下列说法正确的是（ ）
A．的坐标是
B．若点，则周长的最小值是11
C．可能为锐角
D．的最小值是9
61．【多选】（2023春·山东菏泽·高二校考期末）过抛物线上一点A(1，-4)作两条相互垂直的直线，与C的另外两个交点分别为M，N，则（ ）
A．C的准线方程是
B．过C的焦点的最短弦长为8
C．直线MN过定点(0，4)
D．当点A到直线MN的距离最大时，直线MN的方程为
【过关检测】
一、单选题
1．（2023春·北京·高二人大附中校考期末）是抛物线上一点，是抛物线的焦点，则（ ）
A．B．3C．D．4
2．（2023秋·陕西安康·高二校联考期末）已知抛物线与圆交于A，B两点，则（ ）
A．2B．C．4D．
3．（2023春·江苏连云港·高二校考期末）已知抛物线C的焦点是直线与坐标轴的一个交点，则抛物线C的标准方程是（ ）
A．B．C．D．
4．（2023春·安徽宿州·高二校联考期末）已知函数抛物线的焦点为，准线为，点在抛物线上，直线交轴于点，若 ，则点到焦点的距离为（ ）
A．5B．3C．4D．6
5．（2023春·山东·高二沂水县第一中学期末）图1为一种卫星接收天线，其曲面与轴截面的交线为拋物线的一部分，已知该卫星接收天线的口径，深度，信号处理中心位于焦点处，以顶点为坐标原点，建立如图2所示的平面直角坐标系，若是该拋物线上一点，点，则的最小值为（ ）
A．4B．3C．2D．1
二、多选题
6．（2023春·浙江金华·高二浙江金华第一中学校考期末）直线l经过抛物线的焦点F，且与抛物线相交于A，B两点，连接点A和坐标原点O的直线交抛物线准线于点D，则（ ）．
A．F坐标为B．最小值为4
C．一定平行于x轴D．可能为直角三角形
7．（2023春·福建福州·高二福建省福州屏东中学校考期末）已知抛物线的焦点为，，是抛物线上两点，则下列结论正确的是（ ）
A．点的坐标为
B．若直线过点，则
C．若，则的最小值为
D．若，则线段的中点到轴的距离为
三、填空题
8．（2023秋·上海闵行·高二校考期末）过抛物线的焦点且斜率为2的直线与抛物线交于两点，则线段长为___．
9．（2023春·湖北随州·高二随州市曾都区第一中学期末）抛物线的焦点为，为抛物线上一动点，定点，则的最小值为___________.
10．（2023春·安徽蚌埠·高二统考期末）抛物线的准线方程是，则实数___________.
11．（2023春·陕西渭南·高二期末）已知抛物线的准线经过椭圆的焦点，则____________．
四、解答题
12．（2023春·江苏苏州·高二苏州中学校考期末）已知抛物线的焦点为F，点在抛物线C上.
(1)求点F的坐标和抛物线C的准线方程；
(2)过点F的直线l交抛物线C于A、两点，且线段AB的中点为，求直线l的方程及.
13．（2023春·山东·高二沂水县第一中学期末）已知F是抛物线C：的焦点，点M在抛物线C上，且M到F的距离是M到y轴距离的3倍.
(1)求M的坐标；
(2)求直线MF被抛物线C所截线段的长度.
14．（2023春·陕西渭南·高二统考期末）设抛物线的焦点为，过点的直线交抛物线于两点，且，线段的中点到轴的距离为3.
(1)求抛物线的方程；
(2)若直线与圆和抛物线均相切，求实数的值.
15．（2023春·福建·高二福建师大附中校考期末）已知抛物线，点在抛物线上.
(1)求抛物线的方程；
(2)不过原点的直线与抛物线交于不同两点，若以线段为直径的圆过原点，求的值.
16．（2023春·四川泸州·高二四川省泸县第一中学校考期末）已知抛物线上一点到焦点的距离为4.
(1)求抛物线的标准方程；
(2)过焦点的直线与抛物线交于不同的两点,,为坐标原点，设直线，的斜率分别为，，求证：为定值.
标准方程
y2＝2px(p＞0)
y2＝－2px(p＞0)
x2＝2py(p＞0)
x2＝－2py(p＞0)
图形
顶点
O(0,0)
对称轴
x轴
y轴
焦点
Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(p,2)))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，－\f(p,2)))
离心率
e＝1
准线方程
x＝－eq \f(p,2)
x＝eq \f(p,2)
y＝－eq \f(p,2)
y＝eq \f(p,2)
范围
x≥0，y∈R
x≤0，y∈R
y≥0，x∈R
y≤0，x∈R
开口方向
向右
向左
向上
向下
焦半径(其中P(x0，y0))
|PF|＝x0＋eq \f(p,2)
|PF|＝－x0＋eq \f(p,2)
|PF|＝y0＋eq \f(p,2)
|PF|＝－y0＋eq \f(p,2)