七年级数学下学期期末模拟测试卷模拟卷01（浙江杭州卷）（原卷版+解析版）

这是一份七年级数学下学期期末模拟测试卷模拟卷01（浙江杭州卷）（原卷版+解析版），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．下列方程中，是二元一次方程的是（ ）
A．y＝3x﹣1B．xy＝1C．x2D．x+y+z＝1
2．在下列四个图案中，不能通过其中一个小图形通过平移变化得到的是（ ）
A．B．
C．D．
3．若分式有意义，则x应满足的条件是（ ）
A．x≠0B．x≥3C．x≠3D．x≤3
4．下面四个图形中，∠1与∠2是同位角的是（ ）
A．B．
C．D．
5．定义运算a★b＝|ab﹣2a﹣b|，如1★3＝|1×3﹣2×1﹣3|＝2．若a＝2，且a★b＝3，则b的值为（ ）
A．7B．1C．1或7D．3或﹣3
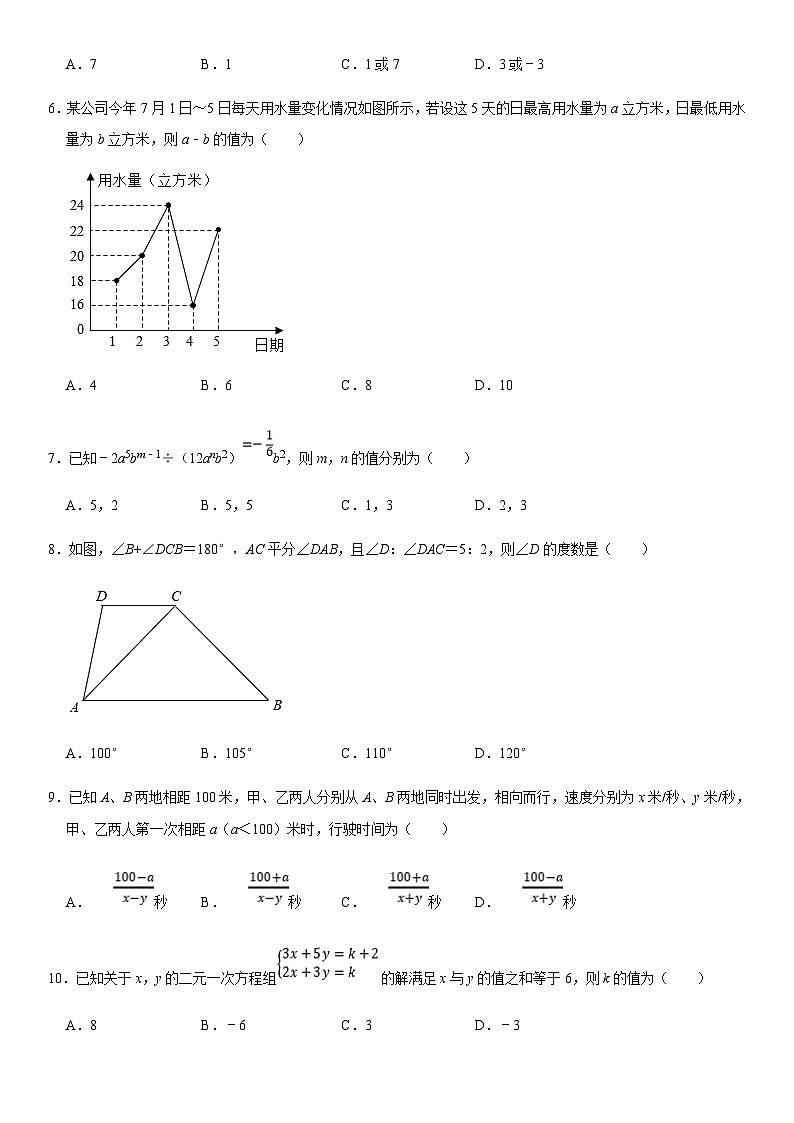
6．某公司今年7月1日～5日每天用水量变化情况如图所示，若设这5天的日最高用水量为a立方米，日最低用水量为b立方米，则a﹣b的值为（ ）
A．4B．6C．8D．10
7．已知﹣2a5bm﹣1÷（12anb2）b2，则m，n的值分别为（ ）
A．5，2B．5，5C．1，3D．2，3
8．如图，∠B+∠DCB＝180°，AC平分∠DAB，且∠D：∠DAC＝5：2，则∠D的度数是（ ）
A．100°B．105°C．110°D．120°
9．已知A、B两地相距100米，甲、乙两人分别从A、B两地同时出发，相向而行，速度分别为x米/秒、y米/秒，甲、乙两人第一次相距a（a＜100）米时，行驶时间为（ ）
A．秒B．秒C．秒D．秒
10．已知关于x，y的二元一次方程组的解满足x与y的值之和等于6，则k的值为（ ）
A．8B．﹣6C．3D．﹣3
二、填空题（本大题共6小题，每小题4分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
11．已知某组数据的频数为63，样本容量为90，则频率为 ．
12．若m+n，m2﹣n2＝3，则m﹣n＝ ．
13．若是方程x+ay＝3的一个解，则a的值为 ．
14．因式分解：mx2﹣mx+m＝ ．
15．某厂计划加工180万个医用口罩，第一周按原计划的速度生产，一周后以原来计划的1.5倍速度生产，结果比原计划提前一周完成任务，则原计划每周生产 万个口罩．
16．已知多项式3xn﹣（m+1）x+1是关于x的三次二项式，m﹣n＝ ．
三、解答题（本大题共7小题，共66分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）因式分解：
（1）（m+n）2﹣4n2；
（2）（x2+y2）2﹣4x2y2．
18．（6分）探索发现：
1；
；
；
根据你发现的规律，回答下列问题：
（1） ； ；
（2）利用发现的规律计算：；
（3）利用以上规律解方程：．
19．（8分）某市为了提高学生的安全防范意识和能力，每年在全市中小学学生中举行安全知识竞赛，为了了解今年全市七年级同学的竞赛成绩情况，小强随机调查了一些七年级同学的竞赛成绩，根据收集到的数据绘制了参与调查学生成绩的频数分布直方图和其中合格学生成绩的扇形统计图如下：
根据统计图提供的信息，解答以下问题：
（1）小强本次共调查了多少名七年级同学的成绩？被调查的学生中成绩合格的频率是多少？
（2）该市若有10000名七年级学生，请你根据小强的调查统计结果估计全市七年级学生中有多少名学生竞赛成绩合格？对此你有何看法？
（3）填写下表：
20．（10分）（1）如图1，已知点A是BC上方的一点，连接AB，AC，求∠B+∠BAC+∠C的度数．
阅读并补充下面的求解过程，
解：过点A画ED∥BC．
根据“ ”，可以得到∠B＝ ，∠C＝∠DAC．
而∠EAB+∠BAC+∠DAC＝180°，所以∠B+∠BAC+∠C＝180°．
（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数（提示：过点C画CF∥AB）．
（3）如图3，AB∥EF，BC⊥DC于点C，设∠B＝x，∠D＝y，∠E＝z，请用一个含x，y，z的等式表示∠B，∠D，∠E三者之间的数量关系．（直接写出结果）
21．（10分）如图，某中学校园内有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，学校计划在中间留一块边长为（a+b）米的正方形地块修建一座雕像，然后将阴影部分进行绿化．
（1）求绿化的面积．（用含a、b的代数式表示）
（2）当a＝2，b＝4时，求绿化的面积．
22．（12分）为拓展学生的知识面，德强中学计划建立图书角打造书香校园，已知建立一个中型图书角需要科技类书籍80本，人文类书籍50本；建立一个小型图书角需要科技类书籍50本，人文类书籍30本．每本科技类书籍的单价比每本人文类书籍的单价的2倍还少5元，建立一个中型图书角比建立一个小型图书角需多用650元．（每本科技类书籍的单价相同，每本人文类书籍单价也相同）．
（1）求每本科技类书籍和每本人文类书籍的单价分别为多少元；
（2）若学校计划用38000元从学府书城购买两种书籍建立中、小型图书角共30个，已知书城每本科技类书籍的进价为13元，每本人文类书籍的进价为9元，则书城一共可以获得的利润为多少元？
23．（14分）如图，在△ABC中，点E在AC边上，连接BE，过点E作DF∥BC，交AB于点D．若BE平分∠ABC，EC平分∠BEF．设∠ADE＝α，∠AED＝β．
（1）当β＝80°时，求∠DEB的度数．
（2）试用含α的代数式表示β．
（3）若β＝kα（k为常数），求α的度数（用含k的代数式表示）．
成绩
不合格
合格但不优秀
合格且优秀
频率
0.2


七年级数学下学期期末模拟测试卷01（浙江杭州卷）
一、选择题（本大题共10小题，每小题3分，共30分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．下列方程中，是二元一次方程的是（ ）
A．y＝3x﹣1B．xy＝1C．x2D．x+y+z＝1
解：A、该方程符合二元一次方程的定义，故本选项符合题意．
B、该方程属于二元二次方程，故本选项不符合题意．
C、该方程属于分式方程，故本选项不符合题意．
D、该方程属于三元一次方程，故本选项不符合题意．
答案：A．
2．在下列四个图案中，不能通过其中一个小图形通过平移变化得到的是（ ）
A．B．
C．D．
解：A、能通过其中一个四边形平移得到，不合题意；
B、不能通过其中一个四边形平移得到，需要一个四边形旋转得到，符合题意；
C、能通过其中一个四边形平移得到，不合题意；
D、能通过其中一个四边形平移得到，不合题意．
答案：B．
3．若分式有意义，则x应满足的条件是（ ）
A．x≠0B．x≥3C．x≠3D．x≤3
解：∵x﹣3≠0，
∴x≠3．
答案：C．
4．下面四个图形中，∠1与∠2是同位角的是（ ）
A．B．
C．D．
解：由同位角的定义可知，
选项A、选项B、选项C中的∠1与∠2都不是同位角；
选项D中的∠1与∠2是直线AB、BC被直线AD所截所得到的同位角；
答案：D．
5．定义运算a★b＝|ab﹣2a﹣b|，如1★3＝|1×3﹣2×1﹣3|＝2．若a＝2，且a★b＝3，则b的值为（ ）
A．7B．1C．1或7D．3或﹣3
解：∵a★b＝3，且a＝2，
∴|2b﹣4﹣b|＝3，
∴2b﹣4﹣b＝3或2b﹣4﹣b＝﹣3，
解得b＝7或b＝1，
答案：C．
6．某公司今年7月1日～5日每天用水量变化情况如图所示，若设这5天的日最高用水量为a立方米，日最低用水量为b立方米，则a﹣b的值为（ ）
A．4B．6C．8D．10
解：在折线图中，最高点对应的数为a＝24，最低点对应的数为b＝16，
则a﹣b＝24﹣16＝8；
答案：C．
7．已知﹣2a5bm﹣1÷（12anb2）b2，则m，n的值分别为（ ）
A．5，2B．5，5C．1，3D．2，3
解：∵﹣2a5bm﹣1÷（12anb2）a5﹣nbm﹣1﹣2b2．
∴5﹣n＝0，m﹣1﹣2＝2，
∴m＝5，n＝5．
答案：B．
8．如图，∠B+∠DCB＝180°，AC平分∠DAB，且∠D：∠DAC＝5：2，则∠D的度数是（ ）
A．100°B．105°C．110°D．120°
解：∵∠B+∠DCB＝180°，
∴AB∥CD．
∴∠D+∠DAB＝180°．
设∠D＝5x，则∠DAC＝2x．
∵AC平分∠DAB，
∴∠DAB＝2∠DAC＝2•2x＝4x．
∵AB∥CD，
∴∠D+∠DAB＝180°．
∴5x+4x＝180°．
∴x＝20°．
∴∠D＝5x＝5×20＝100°．
答案：A．
9．已知A、B两地相距100米，甲、乙两人分别从A、B两地同时出发，相向而行，速度分别为x米/秒、y米/秒，甲、乙两人第一次相距a（a＜100）米时，行驶时间为（ ）
A．秒B．秒C．秒D．秒
解：由题意可得，
两人第一次相距a米的运动时间为秒．
答案：D．
10．已知关于x，y的二元一次方程组的解满足x与y的值之和等于6，则k的值为（ ）
A．8B．﹣6C．3D．﹣3
解：，
①﹣②得，x+2y＝2③，
根据题意可知：x+y＝6④，
③﹣④得，y＝﹣4，
将y＝﹣4代入④，得x＝10，
将x＝10，y＝﹣4代入②，得k＝20﹣12＝8．
答：k的值为：8．
答案：A．
二、填空题（本大题共6小题，每小题4分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
11．已知某组数据的频数为63，样本容量为90，则频率为 0.7 ．
解：这组数据的频率0.7，
答案：0.7．
12．若m+n，m2﹣n2＝3，则m﹣n＝ 6 ．
解：∵m2﹣n2＝3，
∴（m+n）（m﹣n）＝3，
∵m+n，
∴m﹣n＝6．
答案：6．
13．若是方程x+ay＝3的一个解，则a的值为 ﹣1 ．
解：由题意得：2+a×（﹣1）＝3．
∴a＝﹣1．
答案：﹣1．
14．因式分解：mx2﹣mx+m＝ m（x2﹣x+1） ．
解：原式＝m（x2﹣x+1）．
答案：m（x2﹣x+1）．
15．某厂计划加工180万个医用口罩，第一周按原计划的速度生产，一周后以原来计划的1.5倍速度生产，结果比原计划提前一周完成任务，则原计划每周生产 45 万个口罩．
解：设原计划每周生产x万个口罩，则一周后以原来速度的1.5倍生产，每周生产1.5x万个口罩，
依题意，得：1，
解得：x＝45，
经检验，x＝45是原方程的解，
即原计划每周生产45万个口罩，
答案：45．
16．已知多项式3xn﹣（m+1）x+1是关于x的三次二项式，m﹣n＝ ﹣4 ．
解：∵多项式3xn﹣（m+1）x+1是关于x的三次二项式，
∴n＝3，﹣（m+1）＝0，
∴m＝﹣1，
∴m﹣n＝﹣1﹣3＝﹣4．
答案：﹣4．
三、解答题（本大题共7小题，共66分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．因式分解：
（1）（m+n）2﹣4n2；
（2）（x2+y2）2﹣4x2y2．
解：（1）（m+n）2﹣4n2
＝（m+n+2n）（m+n﹣2n）
＝（m+3n）（m﹣n）；
（2）（x2+y2）2﹣4x2y2
＝（x2+2xy+y2）（x2﹣2xy+y2）
＝（x+y）2（x﹣y）2．
18．探索发现：
1；
；
；
根据你发现的规律，回答下列问题：
（1） ； ；
（2）利用发现的规律计算：；
（3）利用以上规律解方程：．
解：（1），；
答案：，；
（2）
＝1
＝1
；
（3），
（）（）（），
（），
，
∴．
∴x+50＝3x．
解的x＝25．
经检验，x＝25是原分式方程的解．
∴x＝25．
19．某市为了提高学生的安全防范意识和能力，每年在全市中小学学生中举行安全知识竞赛，为了了解今年全市七年级同学的竞赛成绩情况，小强随机调查了一些七年级同学的竞赛成绩，根据收集到的数据绘制了参与调查学生成绩的频数分布直方图和其中合格学生成绩的扇形统计图如下：
根据统计图提供的信息，解答以下问题：
（1）小强本次共调查了多少名七年级同学的成绩？被调查的学生中成绩合格的频率是多少？
（2）该市若有10000名七年级学生，请你根据小强的调查统计结果估计全市七年级学生中有多少名学生竞赛成绩合格？对此你有何看法？
（3）填写下表：
解：（1）400+100＝500，；
（2）10000×0.8＝8000，
还有2000人成绩不合格，中学生要加强安全知识学习．
（3）合格但不优秀的人数是：400×90%＝360人．
则合格但不优秀的频率是：360÷500＝0.72；
合格且优秀的人数是：400×10%＝40人，
则合格且优秀的频率是：40÷500＝0.08．
20．（1）如图1，已知点A是BC上方的一点，连接AB，AC，求∠B+∠BAC+∠C的度数．
阅读并补充下面的求解过程，
解：过点A画ED∥BC．
根据“ 两直线平行，内错角相等 ”，可以得到∠B＝ ∠BAE ，∠C＝∠DAC．
而∠EAB+∠BAC+∠DAC＝180°，所以∠B+∠BAC+∠C＝180°．
（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数（提示：过点C画CF∥AB）．
（3）如图3，AB∥EF，BC⊥DC于点C，设∠B＝x，∠D＝y，∠E＝z，请用一个含x，y，z的等式表示∠B，∠D，∠E三者之间的数量关系．（直接写出结果）
（1）两直线平行，内错角相等，∠BAE，
（2）过点C画CF∥AB，
∠B+∠BCD+∠D＝∠B+∠BCF+∠DCF+∠D，
两直线平行，同旁内角互补，
∠B+∠BCF+∠DCF+∠D＝180°+180°＝360°，
∠B+∠BCD+∠D＝360°，
（3）过点C画CG∥AB，过点D画DH∥AB，如图
∠BCG＝∠B＝x，∠CDH＝∠DCG＝90°﹣x，
∠E＝∠EDH＝y﹣（90°﹣x）＝x+y﹣90°，
x+y﹣∠E＝90°，
即∠B+∠D﹣∠E＝90°．
21．如图，某中学校园内有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，学校计划在中间留一块边长为（a+b）米的正方形地块修建一座雕像，然后将阴影部分进行绿化．
（1）求绿化的面积．（用含a、b的代数式表示）
（2）当a＝2，b＝4时，求绿化的面积．
解：（1）依题意得：
（3a+b）（2a+b）﹣（a+b）2
＝6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2
＝（5a2+3ab）平方米．
答：绿化面积是（5a2+3ab）平方米；
（2）当a＝2，b＝4时，原式＝20+24＝44（平方米）．
答：绿化面积是44平方米．
22．为拓展学生的知识面，德强中学计划建立图书角打造书香校园，已知建立一个中型图书角需要科技类书籍80本，人文类书籍50本；建立一个小型图书角需要科技类书籍50本，人文类书籍30本．每本科技类书籍的单价比每本人文类书籍的单价的2倍还少5元，建立一个中型图书角比建立一个小型图书角需多用650元．（每本科技类书籍的单价相同，每本人文类书籍单价也相同）．
（1）求每本科技类书籍和每本人文类书籍的单价分别为多少元；
（2）若学校计划用38000元从学府书城购买两种书籍建立中、小型图书角共30个，已知书城每本科技类书籍的进价为13元，每本人文类书籍的进价为9元，则书城一共可以获得的利润为多少元？
解：（1）设每本科技类书籍的单价为x元，每本人文类书籍的单价为y元，
依题意得：，
，
解得：，
答：每本科技类书籍的单价为15元，每本人文类书籍的单价为10元．
（2）设计划建立m个中型图书角，n个小型图书角，
依题意得：，
解得：，
∴（15﹣13）×（80×10+50×20）+（10﹣9）×（50×10+30×20）＝4700（元），
即书城一共可以获得的利润为4700元．
23．如图，在△ABC中，点E在AC边上，连接BE，过点E作DF∥BC，交AB于点D．若BE平分∠ABC，EC平分∠BEF．设∠ADE＝α，∠AED＝β．
（1）当β＝80°时，求∠DEB的度数．
（2）试用含α的代数式表示β．
（3）若β＝kα（k为常数），求α的度数（用含k的代数式表示）．
解：（1）∵β＝80°，
∴∠CEF＝∠AED＝80°，
∵EC平分∠BEF，
∴∠BEC＝∠CEF＝80°，
∴∠DEB＝180°﹣80°﹣80°＝20°；
（2）∵DF∥BC，
∴∠ADE＝∠ABC＝α，
∵BE平分∠ABC，
∴∠DEB＝∠EBC，
∵EC平分∠BEF，
∴β＝∠CEF（180°）＝90°α；
（3）∵β＝kα，
∴90°α＝kα，
解得：α．
成绩
不合格
合格但不优秀
合格且优秀
频率
0.2


成绩
不合格
合格但不优秀
合格且优秀
频率
0.2
0.72
0.08