

- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 常用逻辑用语(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
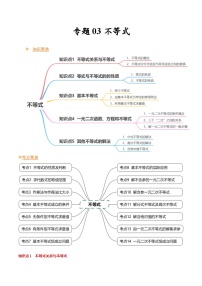
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 不等式(14大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04 函数的概念及表示(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05 函数的基本性质(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06 幂指对函数的图象与性质(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
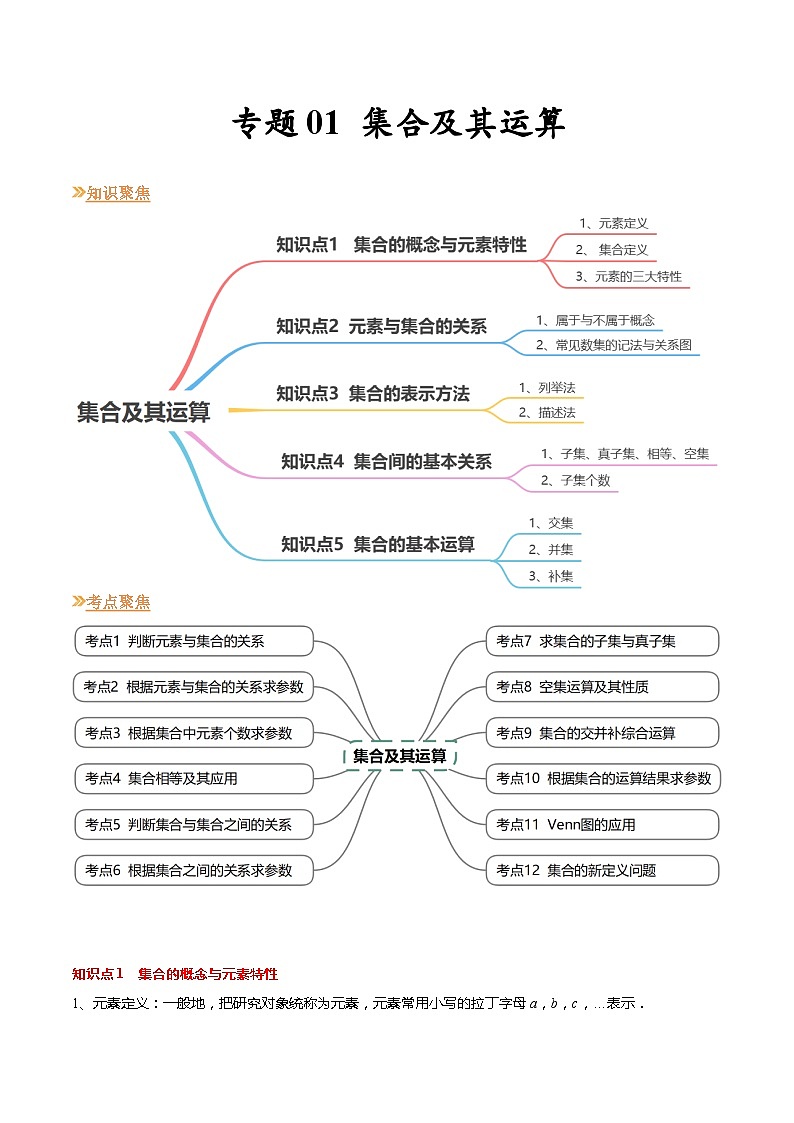
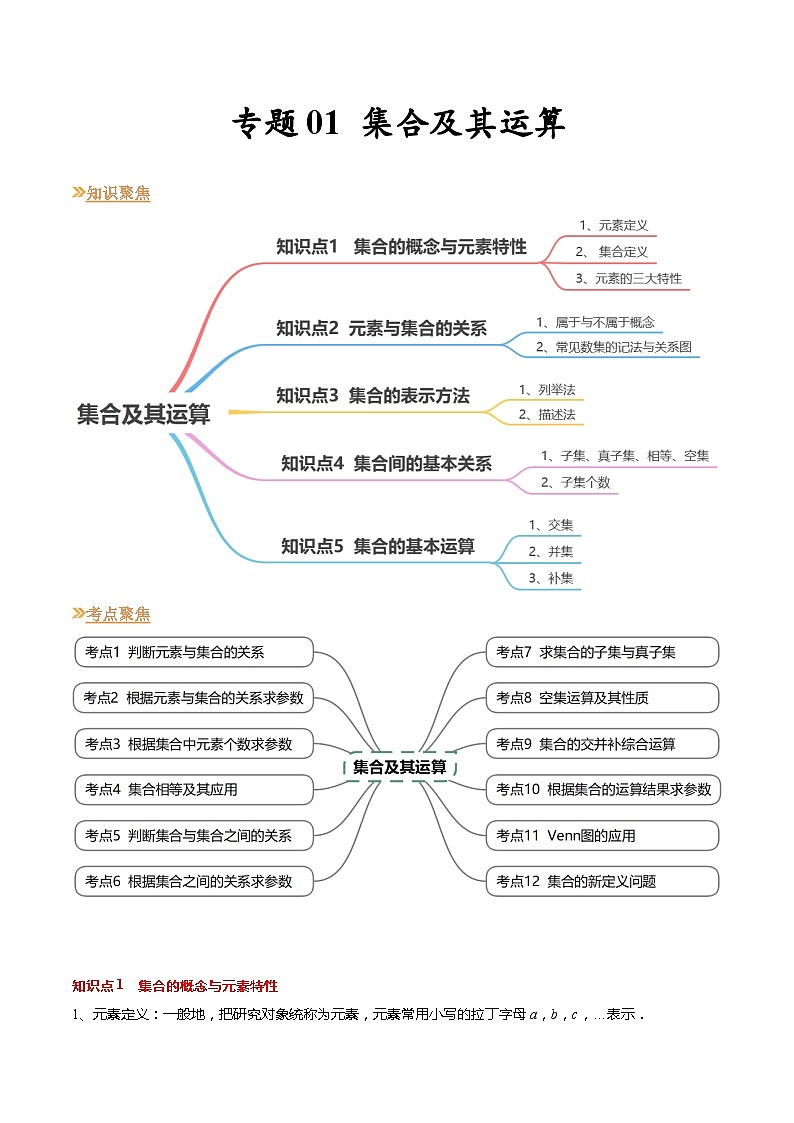
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题01 集合及其运算(12大考点,知识串讲+热考题型+专题训练)-
展开知识聚焦
考点聚焦
知识点1 集合的概念与元素特性
1、元素定义:一般地,把研究对象统称为元素,元素常用小写的拉丁字母a,b,c,…表示.
2、集合定义:把一些元素组成的总体叫做集合(简称为集),集合通常用大写的拉丁字母A,B,C,…表示.
3、元素的三大特性
(1)确定性:给定的集合,它的元素必须是确定的.也就是说,任何一个元素在不在这个集合中是确定的.
(2)互异性:一个给定集合中的元素是互不相同的.也就是说,集合中的元素是不重复出现的.
(3)无序性:给定集合中的元素是不分先后,没有顺序的.
知识点2 元素与集合的关系
1、属于与不属于概念:
(1)属于:如果a是集合A的元素,就说a属于集合A,记作a∈A.
(2)不属于:如果a不是集合A的元素,就说a不属于集合A,记作a∉A.
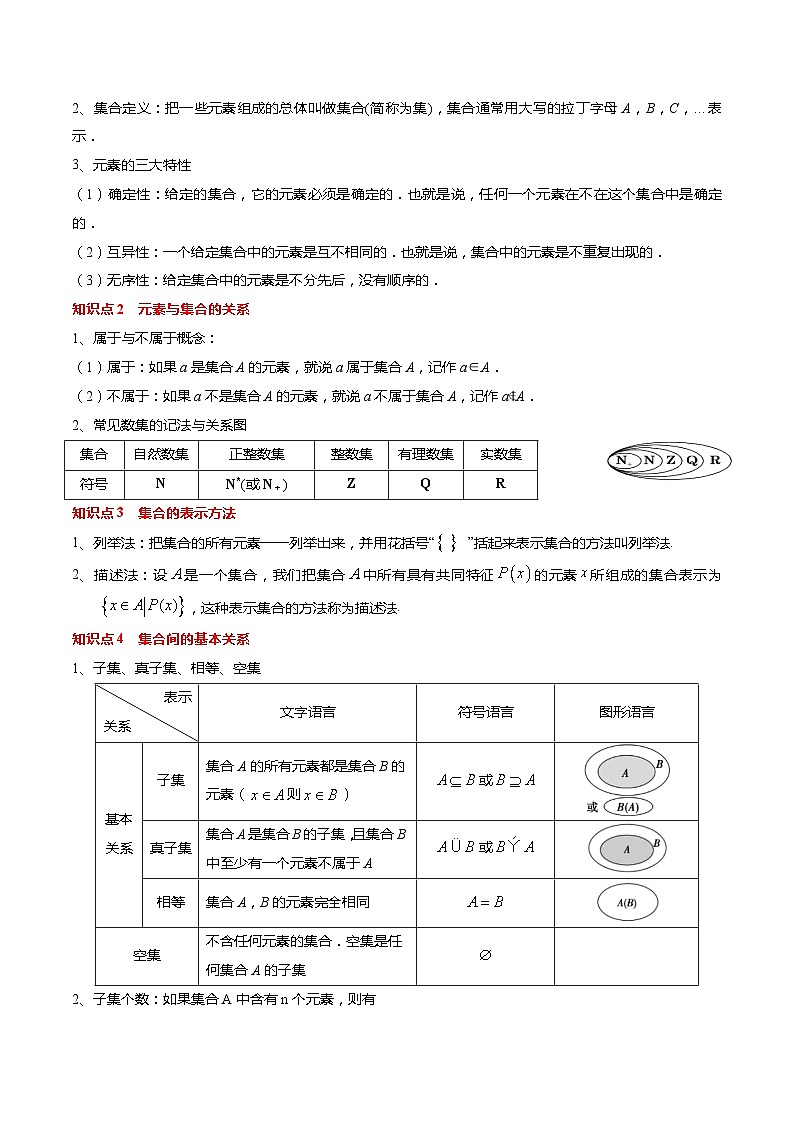
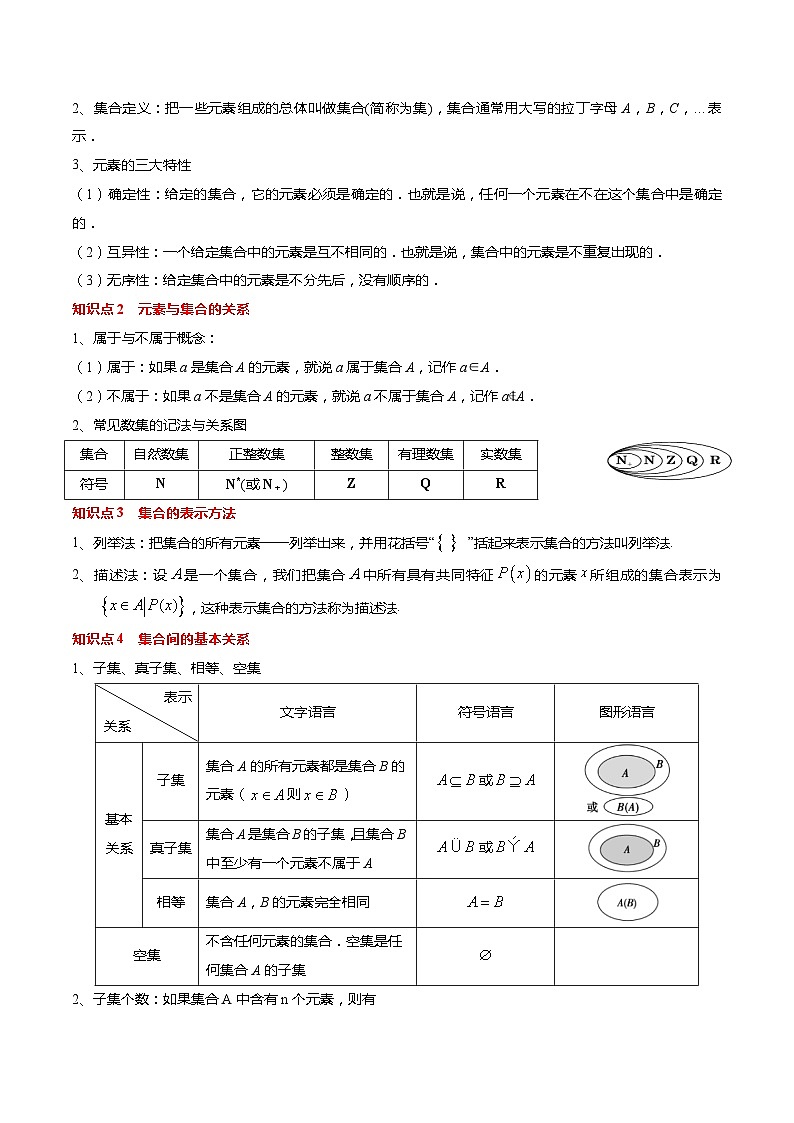
2、常见数集的记法与关系图
知识点3 集合的表示方法
1、列举法:把集合的所有元素一一列举出来,并用花括号“ ”括起来表示集合的方法叫列举法.
2、描述法:设是一个集合,我们把集合中所有具有共同特征的元素所组成的集合表示为,这种表示集合的方法称为描述法.
知识点4 集合间的基本关系
1、子集、真子集、相等、空集
2、子集个数:如果集合A中含有n个元素,则有
(1)A的子集的个数有2n个.
(2)A的非空子集的个数有2n-1个.
(3)A的真子集的个数有2n-1个.
(4)A的非空真子集的个数有2n-2个.
知识点5 集合的基本运算
1、并集:由所有属于集合或集合的元素组成的集合,称为集合与的并集.
记作:,即.
2、交集:由属于集合A且属于集合B的所有元素组成的集合,称为集合与的交集.
记作:,即.
3、补集:对于集合A,由全集U中不属于集合A的所有元素组成的集合,称为集合A相对于全集U的补集,记作:,即.
考点剖析
考点1 判断元素与集合的关系
【例1】(2023秋·全国·高一专题练习)给出下列关系:①;②;③;④.其中正确的个数为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】显然都是实数,①正确,②错误;
是自然数,③正确;是无理数,不是有理数,④错误,
所以正确的个数为2.故选:B
【变式1-1】(2023秋·吉林长春·高一东北师大附中校考阶段练习)已知集合,则必有( )
A. B. C. D.
【答案】C
【解析】因为,
因为,,,,所以C正确,ABD错误,故选:C
【变式1-2】(2023秋·高一课时练习)已知,那么( )
A. B. C. D.
【答案】A
【解析】由题意可得所以,故选:A
【变式1-3】(2023秋·全国·高一专题练习)已知集合且,则下列判断不正确的是( )
A. B. C. D.
【答案】D
【解析】根据集合可知,
集合表示奇数集,集合表示偶数集,又,所以是奇数,是偶数;
对于A,因为两个奇数的乘积为奇数,所以,即A正确;
对于B,因为一个奇数和一个偶数的乘积为偶数,所以,即B正确;
对于C,因为两个奇数的和为偶数,所以,即C正确;
对于D,因为两个奇数与一个偶数的和为偶数,所以,所以D错误;故选:D
【变式1-4】(2023秋·高一课时练习)(多选)下列结论中,不正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】AB
【解析】在A中,当时,显然不成立.
对于B,当,其平方数仍为整数, 显然不成立;
对于C,当,其绝对值仍为有理数, 正确;
对于D项,当,其立方仍为实数,正确.故选:AB.
考点2 根据元素与集合的关系求参数
【例2】(2023春·甘肃白银·高二校考阶段练习)已知集合,若,则实数的取值范围为( )
A. B. C. D.
【答案】A
【解析】因为集合,且,
所以,即,解得或.故选:A.
【变式2-1】(2023秋·广东惠州·高三统考阶段练习)集合 ,若且,则的取值范围为( )
A. B. C. D.
【答案】B
【解析】因为且,所以且,解得.故选:B.
【变式2-2】(2023秋·吉林白城·高三校考阶段练习)已知集合中的最大元素为,则实数 .
【答案】1
【解析】因为,所以,
所以,解得或,
显然不满足集合元素的互异性,故舍去,经检验符合题意.
故答案为:
【变式2-3】(2023秋·甘肃·高一校考阶段练习)(多选)已知集合,若,则实数a的可能取值为( )
A.-2 B.0 C.2 D.4
【答案】AB
【解析】当,即时,,符合题意;
当,即时,不符合题意;
当,即或时.若,不符合题意;
若,,符合题意.故选:AB.
【变式2-4】(2023·江苏·高一专题练习)(多选)已知集合A中有个元素,,,且当时,,则可能为( )
A. B. C. D.或或
【答案】AB
【解析】对于A,当时,,满足题意,A正确;
对于B,当时,,满足题意,B正确;
对于C,当时,,不合题意,C错误;
对于D,由ABC知:或,D错误.故选:AB.
考点3 根据集合中元素个数求参数
【例3】(2022·全国·高一专题练习)若集合,则实数的取值范围是( )
A. B. C. D.,
【答案】C
【解析】,∴方程无解,即,
解得:,则实数的范围为,故选:C.
【变式3-1】(2022秋·河北衡水·高一校考阶段练习)(多选)已知集合,则满足中有8个元素的的值可能为( )
A.6 B. C.8 D.9
【答案】ABC
【解析】当时,满足的有6,3,2,1,,,,,
即集合中有8个元素,符合题意,故A可选,
当时,满足的有6,3,2,1,,,,,
即集合中有8个元素,符合题意,故B可选,
当时,满足的有8,4,2,1,,,,,
即集合中有8个元素,符合题意,故C可选,
当时,满足的有9,3,1,,,,
即集合中有6个元素,不符合题意,故D不可选,故选:ABC.
【变式3-2】(2023秋·甘肃武威·高一校考阶段练习)(多选)已知集合中只有一个元素,则实数a的可能取值为( )
A.0 B.1 C.2 D.4
【答案】ABD
【解析】当时,,解得,所以,符合题意;
当时,由题意,得,解得或.故选:ABD
【变式3-3】(2023秋·河南商丘·高一校考阶段练习)若集合中有2个元素,求k的取值范围.
【答案】且.
【解析】由题意得且,解得且.
故实数k的取值范围为且.
【变式3-4】(2022秋·湖南长沙·高一校考阶段练习)已知全集,.
(1)若中有个元素,求实数的值;
(2)若中有四个元素,求实数的值.
【答案】(1);(2)
【解析】(1)由中有个元素,集合中有两个元素,
即方程有两个不等的实根,,
则,且,,
则,;
(2)由中有四个元素,则集合中有且只有一个元素,
则方程有且只有一个实数根,
则,且,
则,.
考点4 集合相等及其应用
【例4】(2023秋·贵州遵义·高一校考阶段练习)(多选)给出以下几组集合,其中是相等集合的有( )
A., B.,
C., D.,
【答案】CD
【解析】对于A,是点集,是数集,,故A错误;
对于B,,故B错误;
对于C,,,故C正确;
对于D,,
,故D正确.故选:CD.
【变式4-1】(2022秋·全国·高一阶段练习)(多选)下列集合中,与相等的是( )
A. B. C. D.
【答案】BC
【解析】对于A选项,,A不满足条件;
对于B选项,,B满足条件;
对于C选项,,C满足条件;
对于D选项,,D不满足条件.故选:BC.
【变式4-2】(2023秋·宁夏银川·高一校考阶段练习)已知集合,,,则的值为( )
A.3 B. C.1 D.
【答案】A
【解析】因为集合,,,
所以,即,
所以,因为,所以的值为.故选:A .
【变式4-3】(2023·全国·高一专题练习)已知实数集合若,则( )
A. B.0 C.1 D.2
【答案】A
【解析】由题意可知,两集合元素全部相等,
得到或
又根据集合互异性,可知,解得或(舍),
所以故选:A.
【变式4-4】(2023秋·山东菏泽·高一校考阶段练习)已知,,若集合,则的值为( )
A. B. C.1 D.2
【答案】B
【解析】根据题意,,故,则,
则,由集合的互异性知且,
故,则, 即或(舍),
当时,,符合题意,
所以.故选:B.
考点5 判断集合与集合之间的关系
【例5】(2023·全国·高一专题练习)(多选)已知集合,则下列关系正确的是( )
A. B. C. D.A
【答案】CD
【解析】因为集合,
所以根据子集及真子集的定义可知A .故选:CD.
【变式5-1】(2023秋·江西·高三统考开学考试)已知全集,若集合满足,则( )
A. B. C. D.
【答案】D
【解析】依题意,,
又,则或,
因此,,不是的子集,
,即ABC错误,D正确.故选:D
【变式5-2】(2023秋·山西晋城·高三校考阶段练习)设集合,,则( )
A. B. C. D.
【答案】C
【解析】对任意,则存在,使得,显然,因此,
但,而,所以是的子集也是真子集,四个选项中只有C正确,故选:C.
【变式5-3】(2021秋·高一课时练习)已知集合,,则M,P之间的关系为( )
A.M=P B. C. D.
【答案】B
【解析】因为,
,
所以.故选:B.
【变式5-4】(2023秋·全国·高一专题练习)已知集合,,,则,,的关系为( )
A. B. C. D.
【答案】B
【解析】因为,
,
,
且,,,,
,,所以.故选:B
考点6 根据集合之间的关系求参数
【例6】(2023秋·江苏连云港·高一校考开学考试)(多选)已知集合,,若,则实数a的值可以是( )
A.0 B. C.2 D.
【答案】ABD
【解析】由,得到或,即,
因为,由,
当时,无解,此时,满足题意,
当时,得到,所以或,得到或,故选:ABD.
【变式6-1】(2023秋·甘肃武威·高一校考阶段练习)已知集合,,若,则实数m的取值范围是( )
A. B. C. D.
【答案】C
【解析】.
若,则,解得,符合题意;
若时,则解得.
综上,实数m的取值范围是.故选:C.
【变式6-2】(2023秋·江苏连云港·高一校考开学考试)已知集合,,且,则实数m的取值范围是( )
A. B. C. D.
【答案】A
【解析】因为,所以,
又,,所以,得到,故选:A.
【变式6-3】(2023·上海·高一专题练习)已知,.
(1)若是的子集,求实数的值;
(2)若是的子集,求实数的取值范围.
【答案】(1);(2)或
【解析】(1)因为,
若是的子集,则,
所以,解得.
(2)若是的子集,则.
①若为空集,则,解得;
②若为单元素集合,则,解得.
将代入方程,得,解得,
所以,符合要求;
③若为双元素集合,,则.
综上所述,或.
【变式6-4】(2022秋·河南商丘·高一校考阶段练习)已知集合,集合.
(1)当时,求;
(2)若,求实数的取值范围.
【答案】(1);(2)
【解析】(1)当时,,已知,
由.
(2),
若,则,解得.
考点7 求集合的子集与真子集
【例7】(2024秋·江西·高三校联考阶段练习)已知集合,,则的真子集的个数为( )
A.6 B.7 C.8 D.15
【答案】B
【解析】因为,
又,
所以,所以的真子集有个.故选:B
【变式7-1】(2023秋·辽宁大连·高一校考阶段练习)设集合,,记,则集合的真子集个数是( )
A.3 B.4 C.7 D.8
【答案】C
【解析】.
集合的真子集个数是:.故选:C.
【变式7-2】(2023秋·四川南充·高一校考阶段练习)已知集合,,则集合的真子集的个数为( )
A.3 B.6 C.7 D.8
【答案】C
【解析】因为,,所以,
所以集合的真子集的个数为,故选:C
【变式7-3】(2023秋·江苏泰州·高一校考阶段练习)满足的集合的个数有( )个
A.8 B.7 C.6 D.5
【答案】B
【解析】集合A中一定含有1,2,3,可能含有4,5,6,但不能同时含有4,5,6.
由此可得到满足条件的集合A的个数就是集合的真子集个数,共有个.故选:B
【变式7-4】(2023秋·山东菏泽·高一校考阶段练习)(多选)若{1,2}⊆B {1,2,3,4},则B=( )
A.{1,2} B.{1,2,3} C.{1,2,4} D.{1,2,3,4}
【答案】ABC
【解析】∵{1,2}⊆B{1,2,3,4},
∴B={1,2}或B={1,2,3}或B={1,2,4},故选:ABC
考点8 空集的运算及其性质
【例8】(2022秋·河北承德·高一校考期末)有下列关系式:①;②;③;④;⑤;⑥.其中不正确的是( )
A.①③④ B.②④⑤ C.②⑤⑥ D.③④
【答案】D
【解析】对①:因为集合元素具有无序性,显然①正确;
对②:因为集合,故正确,即②正确;
对③:空集是一个集合,而集合是以为元素的一个集合,因此,故③不正确;
对④:是一个集合,仅有一个元素0,但是空集不含任何元素,于是,故④不正确;
对⑤:由④可知,非空,于是有,因此⑤正确;
对⑥:显然成立,因此⑥正确.
综上,本题不正确的有③④,故选:D
【变式8-1】(2022秋·吉林·高一校考阶段练习)下列说法正确的是( )
A. B. C. D.
【答案】C
【解析】对于A:,选项A错误;
对于B:是无理数,,选项B错误;
对于C:是它本身的子集,即,选项C正确;
对于D:仅当A为空集时,成立,否则不成立,选项D错误.故选:C.
【变式8-2】(2023·全国·高一专题练习)给出下列说法:
①空集没有子集;
②任何集合至少有两个子集;
③空集是任何集合的真子集;
④若,则.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
【答案】A
【解析】由于任何一个集合都是它本身的子集,空集的子集还是空集,故①不正确;
由于空集的子集还是空集,所以空集的子集只有一个,故②不正确;
由于空集的子集还是空集,但不是真子集,故③不正确;
由于,则或,故④不正确;
综上,正确的说法有0个.故选:A.
【变式8-3】(2023秋·江西新余·高一校考开学考试)(多选)以下四个选项表述正确的有( )
A. B.⫋ C. D.
【答案】BC
【解析】对选项A,由不是的元素,故A错误;
对选项B,由规定:空集是任何集合的子集,则且存在,故⫋,B正确;
对选项C,由子集概念,中的任意一个元素都是的元素,则,C正确;
对选项D,由不是的元素,D错误.故选:BC.
【变式8-4】(2022秋·甘肃酒泉·高一校考期中)已知集合,则实数k的取值范围是 .
【答案】
【解析】∵,∴,解得,
因此实数k的取值范围是.
故答案为:.
考点9 集合的交并补综合运算
【例9】(2023秋·四川成都·高三校考开学考试)设集合,,,则( )
A. B. C. D.
【答案】B
【解析】由,,得,所以,故选:B
【变式9-1】(2023秋·山东·高三校联考阶段练习)已知集合,,则( )
A. B. C. D.
【答案】D
【解析】因为,,所以.故选:D
【变式9-2】(2023春·甘肃平凉·高二校考阶段练习)设已知集合,,则( )
A. B. C. D.
【答案】A
【解析】由,即,解得,
所以,
所以,
又,所以.故选:A
【变式9-3】(2023秋·全国·高一专题练习)已知集合,集合,则下列关系式正确的是( )
A. B.
C.或 D.
【答案】D
【解析】,,
, 故A不正确;
,故B不正确;
或,
或或,故C不正确;
或,故D正确.故选:D.
【变式9-4】(2023秋·宁夏银川·高一校考阶段练习)已知集合,,实数集为全集.
(1)求,; (2)求.
【答案】(1);(2)或
【解析】(1)因为,,
所以;
(2)或,
所以或.
考点10 根据集合的运算结果求参数
【例10】(2023秋·全国·高一专题练习)设集合或,若,则的取值范围是( )
A.或 B.或 C. D.
【答案】B
【解析】由集合或,得,
又集合且,
则2或,即或.故选:B.
【变式10-1】(2022春·四川南充·高一校考开学考试)已知集合,,且,则实数的取值范围为( )
A. B. C. D.
【答案】D
【解析】因为,所以,
又,且,
所以,即实数的取值范围为.故选:D
【变式10-2】(2022春·重庆沙坪坝·高二重庆八中校考期末)已知集合,,若,则实数k的取值范围为 .
【答案】
【解析】由不等式,分解因式可得,解得或,
即或,,
由,.
故答案为:.
【变式10-3】(2023秋·浙江台州·高一统考期末)已知集合,.
(1)若,求;
(2)若,求实数a的取值范围.
【答案】(1);(2)
【解析】(1)若,则,
因为,所以;
(2)由题,得,由,得,
若,则,得,
若,即时,则有,或,得或,
综上,
【变式10-4】(2023秋·吉林长春·高一校考期末)已知集合,集合.
(1)求;
(2)设,若,求实数的取值范围.
【答案】(1)或,;(2)
【解析】(1)依题意,集合,集合,
所以或,.
(2)由(1)得或,
而且,
所以,解得,所以的取值范围是.
考点11 Venn图的应用
【例11】(2023秋·宁夏石嘴山·高三校考阶段练习)已知全集,如图所示,阴影部分表示的集合是( )
A. B. C. D.
【答案】D
【解析】由题图可知,阴影部分表示的集合是,
因为,可得,
所以.故选:D.
【变式11-1】(2022秋·河北保定·高一校考阶段练习)已知全集 ,集合 , ,则如图阴影部分表示的集合是( )
A. B. C. D.
【答案】C
【解析】,
,则.
故阴影部分表示的集合是.故选:C
【变式11-2】(2023秋·全国·高一专题练习)如图,是全集,是的子集,则阴影部分表示的集合是( )
A. B. C. D.
【答案】C
【解析】由图知,阴影部分在集合M中,且在集合P中,但不在集合S中,
故阴影部分所表示的集合是.故选:C.
【变式11-3】(2023秋·四川眉山·高一校考开学考试)(多选)图中矩形表示集合U,两个椭圆分别表示集合M,N,则图中的阴影部分可以表示为( )
A. B. C. D.
【答案】AD
【解析】选项A,,则,故A正确;
选项B,,则,故B错误;
选项C,,,
则,故C错误;
选项D,,,
则,故D正确.故选:AD
【变式11-4】(2023秋·江苏扬州·高三统考开学考试)(多选)已知全集U,集合A,B是U的子集,且,则下列结论中正确的是( )
A. B. C. D.
【答案】AC
【解析】因为,所以,
对于A:由,可得,A正确;
B:由于,故,B错误;
C:因为,,则,C正确;
D:由于,故,D错误.故选:AC.
考点12 集合的新定义问题
【例12】(2023秋·高一课时练习)已知集合,定义集合运算,则 .
【答案】
【解析】由题意知,集合则a与b可能的取值为0,2,3,
∴的值可能为0,2,3,4,5,6,∴
故答案为:
【变式12-1】(2023秋·宁夏·高一校考阶段练习)已知集合,,定义集合,则中元素个数为( )
A.6 B.7 C.8 D.9
【答案】D
【解析】,,
由,
得可取,可取,
所以有个元素.故选:D.
【变式12-2】(2023秋·江苏南京·高一校考阶段练习)设集合M是实数集的子集,如果满足:对任意,都存在,使得,则称t为集合M的聚点,则在下列集合中,以0为聚点的集合有( )
A. B. C. D.
【答案】ACD
【解析】A选项,对于任意,显然,使得,
即0为集合的聚点,A正确;
B选项,对于任意,不妨令,因为,解得,
因为在集合中不存在,故B错误;
C选项,对于任意,存在且,即且时,使得,
即0为集合的聚点,C正确;
D选项,令时,,
对于任意,总存在足够大的使得,
故0为集合的聚点,D正确.故选:ACD
【变式12-3】(2023秋·江苏南通·高一校考阶段练习)已知,对于,若且,则称k为A的“孤立元”.给定集合,则A的所有子集中,只有一个“孤立元”的集合的个数为( )
A.10 B.11 C.12 D.13
【答案】D
【解析】“孤立元”为的集合为,,,,
“孤立元”为的集合为,,
“孤立元”为的集合为,
“孤立元”为的集合为,,
“孤立元”为的集合为,,,,
综上:满足题意的集合有13个.故选:D
【变式12-4】(2023秋·全国·高一专题练习)若X是一个非空集合,是一个以的某些子集为元素的集合,且满足:
(1);
(2)对于的任意子集,当且时,有;
(3)对于的任意子集.当且时,有,则称是集合的一个“——集合类”.
例如: {∅,{b},{c},{b,c},{a,b,c}}是集合的一个“——集合类”.
已知,则所有含的“M——集合类”的个数为( )
A.9 B.10 C.11 D.12
【答案】D
【解析】依题意知,中至少含有这几个元素:,{b,c},{a,b,c},将它看成一个整体;
剩余的{a}、{b}、{c}、{a,c}、{a,b};
①{a}、{b}、{c}、{a,c}、{a,b}5个中添加0个的集合为{,{b,c},{a,b,c}},1种,
②{a}、{b}、{c}、{a,c}、{a,b}5个中添加1个的集合为{,{a},{b,c},{a,b,c}},
{、{b},{b,c},{a,b,c}},{、{c},{b,c},{a,b,c}},共3种,
③{a}、{b}、{c}、{a,c}、{a,b}5个中添加2个的集合共3种,
即{b}、{c};{c}、{a,c};{b}、{a,b}3种添加方式,
④{a}、{b}、{c}、{a,c}、{a,b}5个中添加3个的集合共4种,
即{a}、{b}、{a,b};{a}、{c}、{a,c};{b}、{c}、{a,b};{b}、{c}、{a,c},
共4种添加方式,
⑤{a}、{b}、{c}、{a,c}、{a,b}5个中添加4个的集合共0种,
⑥{a}、{b}、{c}、{a,c}、{a,b}添加5个的集合共1种,
综上含的“M——集合类”的个数为12种.故选:D
过关检测
1.(2023秋·全国·高一专题练习)给出下列关系:①;②;③;④,其中正确的个数为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】是实数,①正确;是无理数,不是有理数,②错误;
是整数,③错误;是无理数,不是自然数,④正确.
正确的个数为2个,故选:B.
2.(2023秋·江苏连云港·高一校考开学考试)若集合,则集合中的元素个数为( )
A.3 B.4 C.5 D.6
【答案】C
【解析】由,即,
所以集合中的元素个数为5个,故选:C.
3.(2023秋·江苏南京·高一校考阶段练习)已知集合,,且,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】因为,,且,
所以,即实数的取值范围是.故选:C
4.(2022秋·河南三门峡·高一校考阶段练习)对任意集合A,下列各式①,②,③,④,正确的个数是( )
A.1 B.2 C.3 D.4
【答案】B
【解析】空集表示无任何元素的集合,所以,①错误;
由交集性质知:,②正确;
由并集性质知,,③正确;
是自然数集,是实数集,所以,④错误.
综上:只有②③正确.故选:B
5.(2022秋·重庆万州·高一校考阶段练习)若则满足条件的集合A的个数是( )
A.9 B.8 C.7 D.6
【答案】B
【解析】因为,
所以或或或或或或或,
即满足条件的集合的个数为8,故选:B.
6.(2023秋·全国·高一专题练习)已知集合,,全集,则以下集合( )是空集
A. B. C. D.
【答案】D
【解析】由得,由得,
故,,,,
仅D选项符合题意.故选:D
7.(2023秋·山西运城·高一校考阶段练习)(多选)考查下列每组对象,能构成集合的是( )
A.中国各地最美的乡村; B.直角坐标系中横、纵坐标相等的点;
C.不小于3的自然数; D.2018年第23届冬季奥运会金牌获得者.
【答案】BCD
【解析】A中“最美”标准不明确,不符合确定性,
B,C,D选项中的元素标准明确,均可构成集合.故选:BCD.
8.(2023·全国·高一专题练习)(多选)集合,则下列关系错误的是( )
A. B. C. D.
【答案】AB
【解析】
时,表示所有奇数,表示所有整数,
所以且,所以CD正确.故选:AB
9.(2023·全国·高一专题练习)(多选)非空集合具有如下性质:①若,则;②若,则.下列判断中,正确的有( )
A. B.
C.若,则 D.若,则
【答案】ABC
【解析】由性质①,若,则没有意义,所以,,则,所以B选项正确.
由性质②,若,而,则,与上述分析矛盾,所以,A选项正确.
若,则;若,则,所以C选项正确.
由,得,则,所以D选项错误.故选:ABC
10.(2023秋·上海浦东新·高一校考阶段练习)已知集合,若,则
【答案】3或
【解析】,,
,解得或,
经检验知或.
11.(2023秋·四川眉山·高一校考开学考试)含有三个实数的集合可表示为,也可以示为,则的值为 .
【答案】0
【解析】因为,且,所以,
则有,
所以,且,得,
所以,
12.(2023秋·辽宁抚顺·高一校考阶段练习)已知集合中有8个子集,则的一个值为 .
【答案】4或9(写出一个即可)
【解析】集合中有8个子集,
由知,集合中有三个元素,则有三个因数,
因为,,
除1和它本身外,还有1个,所以的值可以为4,9.
故答案为:4或9(写出一个即可)
13.(2022秋·天津·高一统考期中)已知全集,集合,集合或.
(1)计算和;
(2)计算和.
【答案】(1) ,或
(2)=;或
【解析】(1)因为,或,
所以,或.
(2)因为,或,
所以或,,
所以=;或.
14.(2023·全国·高一专题练习)已知集合,求:
(1)当时,中至多只有一个元素,求的取值范围;
(2)当满足什么条件时,集合为空集.
【答案】(1)或;(2)或
【解析】(1)由题意得,方程可化为,
①当时,方程可化为,得,所以,符合题意,
②当时,
因为中至多只有一个元素,所以,解得,
综上所述,的取值范围为或;
(2)①当时,方程可化为,因为为空集,所以,
②当时,因为为空集,所以,
综上所述,当或时,集合为空集.
15.(2023秋·陕西榆林·高一校考阶段练习)设集合,,.
(1)若,求实数的值;
(2)若且,求实数的值.
【答案】(1)5;(2)
【解析】(1)由题可得,由,得.
从而,是方程的两个根,即,解得.
(2)因为,.
因为,所以,又,所以,
即,,解得或.
当时,,则,不符合题意;
当时,,则且,故符合题意,
综上,实数的值为.集合
自然数集
正整数集
整数集
有理数集
实数集
符号
N
N*(或N+)
Z
Q
R
表示
关系
文字语言
符号语言
图形语言
基本关系
子集
集合A的所有元素都是集合B的元素(则)
或
真子集
集合A是集合B的子集,且集合B中至少有一个元素不属于A
或
相等
集合A,B的元素完全相同
空集
不含任何元素的集合.空集是任何集合A的子集
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题03向量的数乘6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题03向量的数乘6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。