


- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题01 集合及其运算(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 常用逻辑用语(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04 函数的概念及表示(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05 函数的基本性质(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06 幂指对函数的图象与性质(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
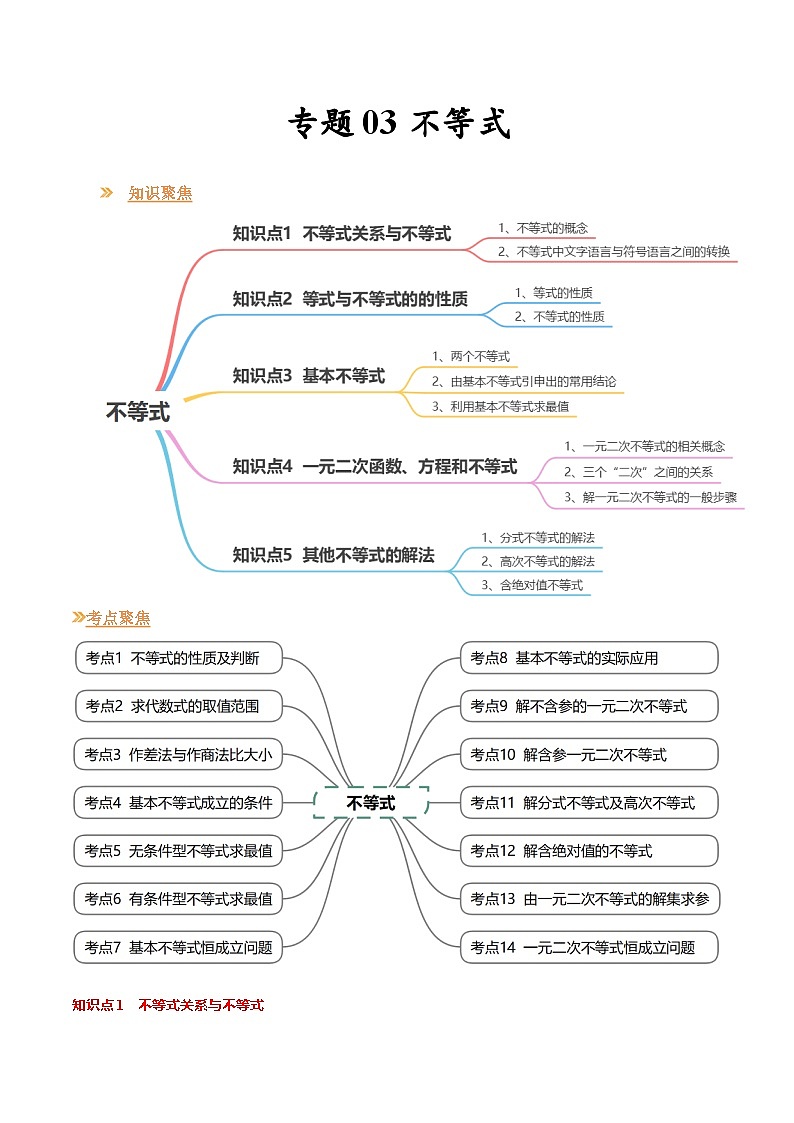
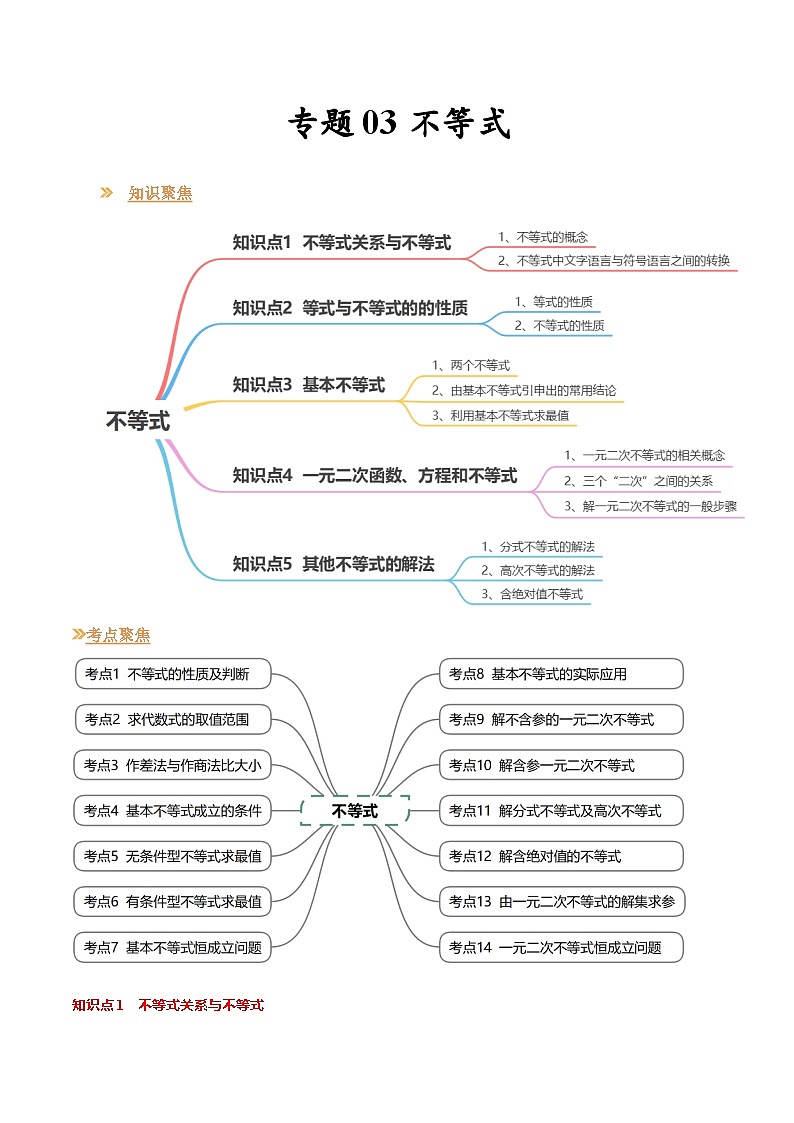
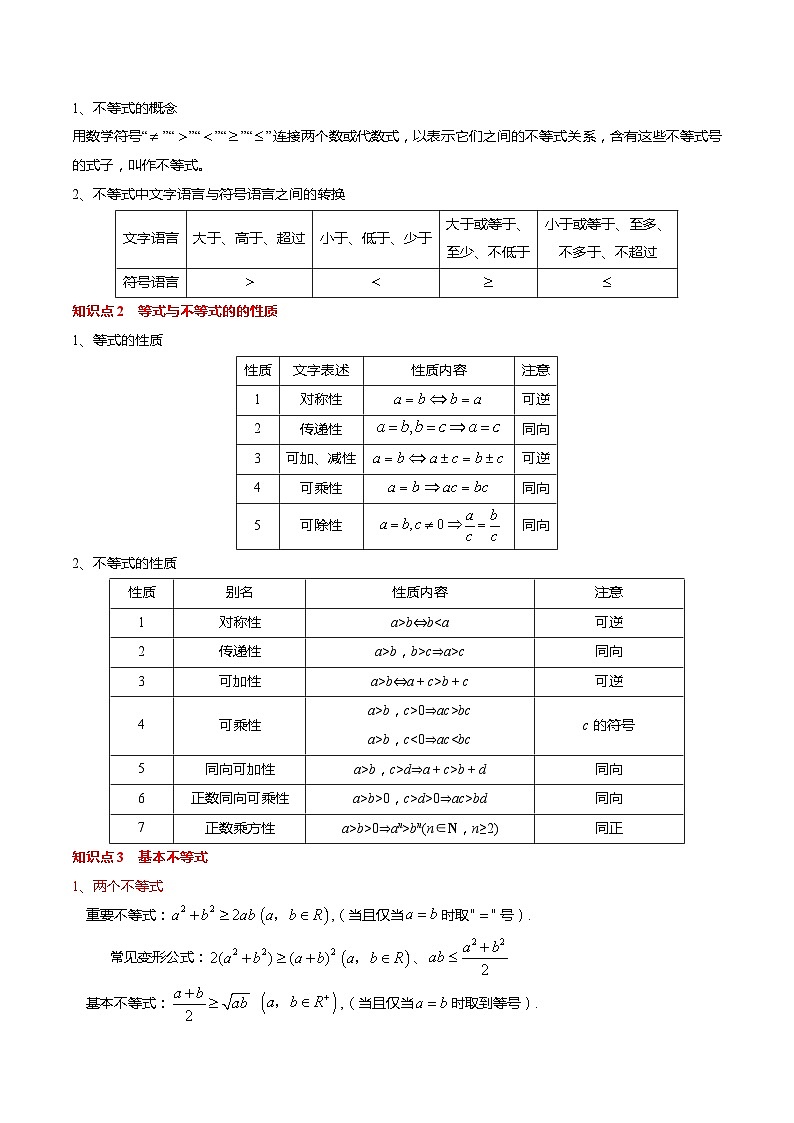
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 不等式(14大考点,知识串讲+热考题型+专题训练)-
展开知识聚焦
考点聚焦
知识点1 不等式关系与不等式
1、不等式的概念
用数学符号“”“”“”“”“”连接两个数或代数式,以表示它们之间的不等式关系,含有这些不等式号的式子,叫作不等式。
2、不等式中文字语言与符号语言之间的转换
知识点2 等式与不等式的的性质
1、等式的性质
2、不等式的性质
知识点3 基本不等式
1、两个不等式
重要不等式:,(当且仅当时取号).
常见变形公式:、
基本不等式: ,(当且仅当时取到等号).
常见变形公式: ;
【注意】(1)成立的条件是不同的:前者只要求都是实数,而后者要求都是正数;
(2)取等号“=” 的条件在形式上是相同的,都是“当且仅当时取等号”.
(3)我们称为的算术平均数,称为的几何平均数.
因此基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数.
2、由基本不等式引申出的常用结论
①(同号);
②(异号);
③或
3、利用基本不等式求最值
(1)在用基本不等式求函数的最值时,要满足三个条件:一正二定三取等.
①一正:各项均为正数;
②二定:含变数的各项的和或积必须有一个为定值;
③三取等:含变数的各项均相等,取得最值.
(2)积定和最小,和定积最大
= 1 \* GB3 ①设x,y为正实数,若x+y=s(和s为定值),则当x=y时,积xy有最大值,且这个值为eq \f(s2,4).
= 2 \* GB3 ②设x,y为正实数,若xy=p(积p为定值),则当x=y时,和x+y有最小值,且这个值为2eq \r(p).
知识点4 一元二次函数、方程和不等式
1、一元二次不等式的相关概念
(1)定义:一般地,只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.
(2)一般形式:ax2+bx+c>0(≥0),ax2+bx+c<0(≤0),(其中a≠0,a,b,c均为常数)
(3)一元二次不等式的解与解集
使某一个一元二次不等式成立的x的值,叫作这个一元二次不等式的解;
一元二次不等式的所有解组成的集合,叫作这个一元二次不等式的解集;
将一个不等式转化为另一个与它解集相同的不等式,叫作不等式的同解变形。
2、二次函数与一元二次方程、不等式的解的对应关系
对于一元二次方程的两根为且,设,它的解按照,,可分三种情况,相应地,二次函数的图像与轴的位置关系也分为三种情况.因此我们分三种情况来讨论一元二次不等式或的解集.
3、解一元二次不等式的一般步骤
(1)判号:检查二次项的系数是否为正值,若是负值,则利用不等式的性质将二次项系数化为正值;
(2)求根:计算判别式,求出相应方程的实数根;
①时,求出两根,且(注意灵活运用因式分解和配方法);
②时,求根;
③时,方程无解
(3)标根:将所求得的实数根标在数轴上(注意两实数根的大小顺序,尤其是当实数根中含有字母时),并画出开口向上的抛物线示意图;
(4)写解集:根据示意图以及一元二次不等式解集的几何意义,写出解集。
口诀:大于零取(根)两边,小于零取(根)中间
知识点5 其他不等式的解法
1、分式不等式的解法:解分式不等式的实质就是讲分式不等式转化为整式不等式。
设A、B均为含x的多项式
(1) (2)
(3) (4)
【注意】当分式右侧不为0时,可过移项、通分合并的手段将右侧变为0;当分母符号确定时,可利用不等式的形式直接去分母。
2、高次不等式的解法
如果将分式不等式转化为正式不等式后,未知数的次数大于2,一般采用“穿针引线法”,步骤如下:
(1)标准化:通过移项、通分等方法将不等式左侧化为未知数的正式,右侧化为0的形式;
(2)分解因式:将标准化的不等式左侧化为若干个因式(一次因式或高次因式不可约因式)的乘积,如的形式,其中各因式中未知数的系数为正;
(3)求根:求如的根,并在数轴上表示出来(按照从小到大的顺序标注)
(4)穿线:从右上方穿线,经过数轴上表示各根的点,(奇穿偶回:经过偶次根时应从数轴的一侧仍回到这一侧,经过奇数次根时应从数轴的一侧穿过到达数轴的另一侧)
(5)得解集:若不等式“>0”,则找“线”在数轴上方的区间;
若不等式“<0”,则找“线”在数轴下方的区间
3、含绝对值不等式
(1)绝对值的代数意义
正数的绝对值是它的本身,负数的绝对值是它的相反数,零的绝对值仍是零.即
(2)绝对值的几何意义:一个数的绝对值,是数轴上表示它的点到原点的距离.
(3)两个数的差的绝对值的几何意义:表示在数轴上,数和数之间的距离.
(4)绝对值不等式:
= 1 \* GB3 ①的解集是,如图1.
= 2 \* GB3 ②的解集是,如图2.
= 3 \* GB3 ③.
= 4 \* GB3 ④或
考点剖析
考点1 不等式的性质及判断
【例1】(2023秋·湖北襄阳·高一校考阶段练习)若,则下列不等式成立的是( )
A. B. C. D.
【变式1-1】(2022秋·山东枣庄·高一校考阶段练习)如果,那么下列不等式中正确的是( )
A. B. C. D.
【变式1-2】(2023春·云南曲靖·高一校考阶段练习)(多选)若,,则下列不等式成立的是( )
A. B. C. D.
【变式1-3】(2023·江苏泰州·高一校考阶段练习)(多选)已知,那么下列结论正确的是( )
A.若,,则 B.若,则
C.若,则 D.若,则
【变式1-4】(2023秋·陕西·高一校考阶段练习)(多选)已知,则下列不等式中错误的是( )
A. B. C. D.
考点2 求代数式的取值范围
【例2】(2023秋·湖北襄阳·高一宜城市第一中学校考阶段练习)已知,,则的取值范围是 .
【变式2-1】(2023秋·四川南充·高一校考阶段练习)已知,,则的取值范围是 .
【变式2-2】(2022秋·青海海东·高一校考阶段练习)(多选)已知,则的取值可以为( )
A.1 B. C.3 D.4
【变式2-3】(2023秋·宁夏银川·高一校考阶段练习)已知,,则的取值范围是( )
A. B. C. D.
【变式2-4】(2023秋·全国·高一专题练习)已知实数,满足,,则的取值范围是( )
A. B. C. D.
考点3 作差法与作商法比大小
【例3】(2023秋·湖北襄阳·高一校考阶段练习)已知,若,,则A与B的大小关系是( )
A.AB C.A=B D.不确定
【变式3-1】(2023秋·四川南充·高一校考阶段练习)已知,设,,则有( )
A. B. C. D.
【变式3-2】(2023秋·四川南充·高一校考阶段练习)设,则 (填“”、“”、“”或“”).
【变式3-3】(2023·全国·高一专题练习)若,则、、、中最小的是 .
【变式3-4】(2020·高一课时练习)若实数,,满足,,,则( )
A. B. C. D.
考点4 基本不等式成立的条件
【例4】(2022秋·广东珠海·高一校考阶段练习)对于,y取最小值时x的值为 .
【变式4-1】(2023·全国·高一专题练习)若,,则当且仅当 时取等号.
【变式4-2】(2023·全国·高一专题练习)不等式中等号成立的条件是 .
【变式4-3】(2023·全国·高一专题练习)下列不等式中等号可以取到的是( )
A. B. C. D.
【变式4-4】(2023秋·广东广州·高一校考期末)(多选)下列命题中正确的是( )
A.时,的最小值是2
B.存在实数,使得不等式成立
C.若,则
D.若,且,则
考点5 无条件型不等式求最值
【例5】(2023·全国·高一专题练习)已知,则的最小值为( )
A.2 B.4 C. D.
【变式5-1】(2023秋·贵州黔西·高三校考阶段练习)的最小值为( )
A.4 B.7 C.11 D.24
【变式5-2】(2023秋·天津·高三校考期末)已知,则的最小值是 .
【变式5-3】(2023·江苏·高一专题练习)已知,,则的最小值为 .
【变式5-4】(2023秋·四川·高一校考阶段练习)已知,则的最小值为( )
A.4 B.6 C. D.10
考点6 有条件型不等式求最值
【例6】(2023秋·广东佛山·高一校考开学考试)已知,,且,则的最大值为( )
A. B. C. D.
【变式6-1】(2023秋·河北邢台·高三联考9月月考)已知正数a,b满足,则的最小值为( )
A.13 B.16 C.9 D.12
【变式6-2】(2023秋·上海松江·高三上海市松江二中校考阶段练习)设正实数x、y、z满足,则的最大值为 .
【变式6-3】(2023秋·安徽亳州·高一校考阶段练习)设均为正数且,则的最小值为( )
A.1 B.3 C. D.2
【变式6-4】(2023秋·全国·高一专题练习)已知且,则的最小值为( )
A.10 B.9 C.8 D.7
考点7 基本不等式恒成立问题
【例7】(2023秋·广西南宁·高二校考开学考试)若,,且,恒成立,则实数的取值范围是( )
A. B.或 C. D.或
【变式7-1】(2023秋·广东潮州·高三统考期末)正实数满足,且不等式恒成立,则实数的取值范围( )
A. B. C. D.
【变式7-2】(2023秋·全国·高一专题练习)已知且,若恒成立,则实数的范围是 .
【变式7-3】(2023秋·河北邢台·高三上9月月考)不等式对所有的正实数,恒成立,则的最大值为( )
A.2 B. C. D.1
考点8 基本不等式的实际应用
【例8】(2023·全国·高一专题练习)在实验课上,小明和小芳利用一个不等臂的天平秤称取药品. 实验一:小明将克的砝码放在天平左盘,取出一些药品放在右盘中使天平平衡;实验二:小芳将克的砝码放在右盘,取出一些药品放在天平左盘中使天平平衡,则在这两个实验中小明和小芳共秤得的药品( )
A.大于克 B.小于克 C.大于等于克 D.小于等于克
【变式8-1】(2023·全国·高一专题练习)某社区计划在一块空地上种植花卉,已知这块空地是面积为1800平方米的矩形,为了方便居民观赏,在这块空地中间修了如图所示的三条宽度为2米的人行通道,则种植花卉区域的面积的最大值是( )
A.1208平方米 B.1448平方米 C.1568平方米 D.1698平方米
【变式8-2】(2023·全国·高一专题练习)奋进新征程,建功新时代.某单位为提升服务质量,花费万元购进了一套先进设备,该设备每年管理费用为万元,已知使用年的维修总费用为万元,则该设备年平均费用最少时的年限为( )
A. B. C. D.
【变式8-3】(2023·全国·高一专题练习)某企业一个月生产某种商品万件时的生产成本为(万元),每件商品售价为元,假设每月所生产的产品能全部售完.当月所获得的总利润用(万元)表示,用表示当月生产商品的单件平均利润,则下列说法正确的是( )
A.当生产万件时,当月能获得最大总利润万元
B.当生产万件时,当月能获得最大总利润万元
C.当生产万件时,当月能获得单件平均利润最大为元
D.当生产万件时,当月能获得单件平均利润最大为元
【变式8-4】(2023秋·高一单元测试)某工厂利用不超过64000元的预算资金拟建一长方体状的仓库,为节省成本,仓库依墙角而建(即仓库有两个相邻的侧面为墙面,无需材料),由于要求该仓库高度恒定,不靠墙的两个侧面按照其底边的长度来计算造价,造价为每米1600元,仓库顶部按面积计算造价,造价为每平方米600元.在预算允许的范围内,仓库占地面积最大为( ).
A.36平方米 B.48平方米 C.64平方米 D.72平方米
考点9 解不含参的一元二次不等式
【例9】(2023秋·宁夏银川·高一校考阶段练习)一元二次不等式的解集为( )
A. B. C. D.
【变式9-1】(2022秋·天津·高一统考期中)不等式的解集是( )
A. B. C.或 D.或
【变式9-2】(2022秋·广东茂名·高一校考期中)不等式的解集是 .
【变式9-3】(2023春·云南曲靖·高一校考阶段练习)解下列一元二次不等式.
(1);
(2).
【变式9-4】(2023秋·湖北宜昌·高一校考阶段练习)解下列不等式
(1)
(2)
考点10 解含参一元二次不等式
【例10】(2023秋·全国·高一专题练习)不等式的解集为( )
A. B. C. D.
【变式10-1】(2023秋·湖北荆州·高一校考阶段练习)若,则关于的不等式的解集为 .
【变式10-2】(2023·全国·高一专题练习)解下列关于的不等式:().
【变式10-3】(2022秋·高一单元测试)解关于x的不等式,.
考点11 解分式不等式与高次不等式
【例11】(2023秋·河北保定·高一校考开学考试)不等式的解集为( )
A. B. C. D.
【变式11-1】(2023秋·北京石景山·高一统考期末)不等式的解集为( )
A. B. C. D.
【变式11-2】(2022秋·河北张家口·高一校考期中)不等式的解集是( )
A. B. C. D.
【变式11-3】(2022秋·陕西宝鸡·高二统考期中)不等式解集为( )
A.或 B.或
C.或 D.或或
【变式11-4】(2023·全国·高一专题练习)不等式的解集为 .
考点12 解含绝对值的不等式
【例12】(2023秋·四川雅安·高一校考开学考试)不等式的解集为( )
A. B. C. D.
【变式12-1】(2023春·浙江杭州·高二统考学业考试)不等式的解集是( )
A.或 B.或
C. D.
【变式12-2】(2023秋·江苏南京·高一校考阶段练习)不等式的解为 .
【变式12-3】(2023·上海虹口·高三校考模拟预测)不等式的解集为 .
【变式12-4】(2023秋·福建宁德·高一校考开学考试)解不等式:
(1);
(2);
考点13 由一元二次不等式的解集求参
【例13】(2023春·新疆喀什·高一校考阶段练习)若不等式的解集为,则实数( )
A.2 B. C.3 D.
【变式13-1】(2023·高一课时练习)已知不等式的解集为,则下列说法错误的是( )
A. B. C. D.
【变式13-2】(2023·全国·高一专题练习)关于的不等式的解集中,恰有2个整数,则的取值范围是( )
A. B.
C.或 D.或
【变式13-3】(2023·江苏·高一专题练习)(多选)若关于的不等式的解集为,则的值不可以是( )
A. B. C. D.
【变式13-4】(2022秋·全国·高一期中)(多选)已知关于x的不等式的解集为,则( )
A.
B.
C.不等式的解集为
D.不等式的解集为
考点14 一元二次不等式恒成立问题
【例14】(2022秋·江西南昌·高一校考阶段练习)若不等式的解集为,则实数的取值范围是( )
A. B. C. D.
【变式14-1】(2023秋·上海静安·高三校考开学考试)设不等式对一切都成立,则的取值范围是 .
【变式14-2】(2023秋·四川雅安·高一校考开学考)(多选)当时,不等式恒成立,则m的范围可以是( )
A. B. C. D.
【变式14-3】(2023·江苏·高一专题练习)不等式,对于任意及恒成立,则实数a的取值范围是( )
A. B. C. D.
【变式14-4】(2023秋·全国·高一专题练习)已知对一切,,不等式恒成立,则实数的取值范围是( )
A. B. C. D.
过关检测
1.(2023秋·全国·高一专题练习)已知,下列选项中正确的是( )
A. B. C. D.
2.(2023·全国·高一专题练习)设,则有( )
A. B. C. D.
3.(2022秋·河北·高一校联考阶段练习)若,且,则下列不等式中不恒成立的是( )
A. B. C. D.
4.(2022秋·安徽宣城·高一校考阶段练习)已知为正实数且,则的最小值为( )
A. B. C. D.3
5.(2022秋·高一单元测试)已知正数满足,则的最小值为( )
A.36 B.42 C.49 D.6
6.(2022秋·全国·高一校联考阶段练习)若,则关于x的不等式的解集是( )
A. B.或 C.或 D.
7.(2022秋·全国·高一阶段练习)(多选)下列函数最小值为2的是( )
A. B. C. D.
8.(2022秋·全国·高一校联考阶段练习)(多选)已知关于x的不等式的解集为或,则( )
A.
B.
C.不等式的解集为
D.不等式的解集为
9.(2023秋·高一单元测试)(多选)不等式对任意的恒成立,则( )
A. B. C. D.
10.(2022秋·高一单元测试)不等式的解集为 .
11.(2023·全国·高一专题练习)已知,则的取值范围为 .
12.(2022秋·湖北武汉·高一武钢三中校考阶段练习)已知正实数,满足,且恒成立,则的取值范围是 .
13.(2023秋·高一单元测试)求解下列不等式的解集:
(1); (2); (3);
(4); (5).
14.(2023秋·高一单元测试)已知关于的不等式的解集为或
(1)求,的值;
(2)当,且满足时,有恒成立,求的取值范围.
15.(2022秋·高一单元测试)(1)若不等式对一切实数恒成立,求实数的取值范围;
(2)解关于的不等式.文字语言
大于、高于、超过
小于、低于、少于
大于或等于、
至少、不低于
小于或等于、至多、
不多于、不超过
符号语言
性质
文字表述
性质内容
注意
1
对称性
可逆
2
传递性
同向
3
可加、减性
可逆
4
可乘性
同向
5
可除性
同向
性质
别名
性质内容
注意
1
对称性
a>b⇔b
2
传递性
a>b,b>c⇒a>c
同向
3
可加性
a>b⇔a+c>b+c
可逆
4
可乘性
a>b,c>0⇒ac>bc
a>b,c<0⇒ac
5
同向可加性
a>b,c>d⇒a+c>b+d
同向
6
正数同向可乘性
a>b>0,c>d>0⇒ac>bd
同向
7
正数乘方性
a>b>0⇒an>bn(n∈N,n≥2)
同正
判别式Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c(a>0)的图象
一元二次方程
ax2+bx+c=0(a>0)的根
有两个不相等的实数根x1,x2(x1
没有实数根
ax2+bx+c>0(a>0)的解集
{x|x
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠-\f(b,2a)))))
R
ax2+bx+c<0(a>0)的解集
{x|x1
∅
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题03向量的数乘6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题03向量的数乘6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。