- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题01 向量的概念(5大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 向量的加减法(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
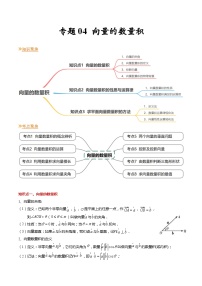
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04++向量的数量积(8大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05+平面向量基本定理(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义
展开知识聚焦
考点聚焦
知识点1 向量的数乘运算
1、向量数乘的定义:规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作:λa,
它的长度与方向规定如下:
(1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向相同;
(3)当λ<0时,λa的方向与a的方向相反.
2、向量数乘的几何意义
当时,把向量沿的相同方向放大或缩小;
当时,把向量沿的相反方向放大或缩小。
3、向量数乘的运算律:设λ,μ为任意实数,则有:
①λ(μ a)=(λμ)a; ②(λ+μ)a=λa+μ a; ③λ(a+b)=λa+λb;
特别地,有(-λ)a=λ(-a)=-(λa); λ(a-b)=λa-λb.
4、向量的线性运算:向量的加、减、数乘运算统称为向量的线性运算,向量线性运算的结果仍是向量.
对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a+μ2b)=λμ1a±λμ2b.
知识点2 向量共线定理
1、向量共线的条件
(1)当向量时,与任一向量共线.
(2)当向量时,对于向量.如果有一个实数,使,那么由实数与向量的积的定义知与共线.
反之,已知向量与()共线且向量的长度是向量的长度的倍,即,那么当与同向时,;当与反向时,.
2、向量共线的判定定理:是一个非零向量,若存在一个实数,使,则向量与非零向量共线.
3、向量共线的性质定理:若向量与非零向量共线,则存在一个实数,使.
【注意】
(1)两个向量定理中向量均为非零向量,即两定理均不包括与共线的情况;
(2)是必要条件,否则,时,虽然与共线但不存在使;
(3)有且只有一个实数,使.
(4)是判定两个向量共线的重要依据,其本质是位置关系与数量关系的相互转化,体现了数形结合的高度统一.
4、向量共线的常用结论
(1)设,均为实数,若,不共线,点满足,,则三点共线;
(2)中线向量公式:在中,若是的中点,则;
(3)与同方向的单位向量为,与共线的单位向量为;
(4)是的重心的充要条件是
考点剖析
考点1 向量数乘的基本运算
【例1】(2023·重庆綦江·高一校考期中)化简为( )
A. B. C. D.
【变式1-1】(2023·高一课时练习)已知向量,那么等于( )
A. B. C. D.
【变式1-2】(2023·全国·高一课时练习)设是两两不共线的向量,且向量,,则( )
A. B. C. D.
【变式1-3】(2023·高一课时练习)(1)已知向量,,计算:.
(2)若向量,满足,,、为已知向量,求向量,.
【变式1-4】(2023·全国·高一随堂练习)求下列未知向.
(1);
(2);
(3).
考点2 用已知向量表示其他向量
【例2】(2023·新疆阿克苏·高一校考阶段练习)在中,点为边的中点,记,则( )
A. B. C. D.
【变式2-1】(2023·江苏连云港·高一统考期中)已知中,,则( )
A. B. C. D.
【变式2-2】(2023·北京顺义·高一牛栏山一中校考期中)如图所示,在中,点是线段上靠近的三等分点,点是线段的中点,则( )
A. B. C. D.
【变式2-3】(2023·福建三明·高一统考期末)在平行四边形ABCD中,,,G为EF的中点,则( )
A. B. C. D.
【变式2-4】(2023·河南周口·高一太康县第一高级中学校考阶段练习)如图所示平行四边形中,设向量,,又,,用,表示、、.
考点3 用向量共线证明三点共线
【例3】(2023·重庆·高二校考期中)已知空间向量,,且,,,则一定共线的三点是( )
A. B. C. D.
【变式3-1】(2023·河南许昌·高二统考期末)已知空间向量,,且,,,则一定共线的三点是( )
A. B. C. D.
【变式3-2】(2023·全国·高一课时练习)已知是平面内两个不共线的向量,,,且三点共线,则( )
A. B.2 C.4 D.
【变式3-3】(2023·江苏镇江·高一统考期末)设与是两个不共线向量,向量,,,若,,三点共线,则( )
A. B. C. D.3
【变式3-4】(2023·广东广州·高一广州市第五中学校考阶段练习)设,是两个不共线的向量,已知,,,若三点A,B,D共线,则k的值为( )
A.-8 B.8 C.6 D.-6
考点4 利用向量共线求参数
【例4】(2023·山西运城·高一统考期中)已知向量,不共线,且向量与方向相同,则实数的值为( )
A.1 B. C.1或 D.1或
【变式4-1】(2023·黑龙江哈尔滨·高一哈尔滨三中校考期末)已知,是两个不共线的向量,向量,.若,则( )
A. B. C. D.
【变式4-2】(2023·辽宁辽阳·高一统考期末)已知向量不共线,,,,则实数 .
【变式4-3】(2023·山西朔州·高一校考阶段练习)已知两个非零向量不共线,且与共线,求实数k的值.
【变式4-4】(2023·四川成都·高一树德中学校考期末)设,是两个不共线的向量,且向量与是平行向量,则实数的值为( )
A. B.1 C.1或 D.或
考点5 向量共线定理推论应用
【例5】(2023·全国·高一随堂练习)在中,D为CB上一点,E为AD的中点,若,则 .
【变式5-1】(2022·陕西渭南·高三校考期末)如图所示,中为重心,过点,,,则 .
【变式5-2】(2023·全国·高一课时练习)已知平行四边形,若点是边的三等分点(靠近点处),点是边的中点,直线与相交于点,则( )
A. B. C. D.
【变式5-3】(2023·广西玉林·高一博白县中学校考开学考试)如图,在中,中线AD、BE、CF相交于点G,点G称为的重心,那么是( )
A.3∶2 B.2∶1 C.3∶1 D.4∶3
【变式5-4】(2024·全国·高一课时练习)已知点G是的重心,过点G作直线分别与两边交于两点(点与点不重合),设,,则的最小值为( )
A.1 B. C.2 D.
考点6 向量线性运算的几何应用
【例6】(2023·高一单元测试)已知点O为所在平面上一点,且满足,若的面积与的面积比值为,则的值为( )
A. B. C.2 D.3
【变式6-1】(2023·高一单元测试)(多选)已知,若点满足,则下列说法正确的是( )
A.点一定在内部 B.
C. D.
【变式6-2】(2023·安徽芜湖·高一安徽师范大学附属中学校考期中)(多选)在中,,以下结论正确的是( )
A. B. C. D.
【变式6-3】(2023·甘肃·高一校联考阶段练习)(多选)设点是所在平面内一点,则下列说法正确的是( )
A.若,则点是的中点
B.若,则点在边的延长线上
C.若,则点是的重心
D.若,则
【变式6-4】(2023·全国·高一课时练习)如图,四边形ABCD是平行四边形,E,F分别是AD,DC的中点,BE,BF分别交AC于M,N.求证:M,N三等分AC.
过关检测
一、单选题
1.(2023·高一课时练习)已知m、n是实数,、是向量,对于命题:
① ②
③若,则 ④若,则
其中正确命题的个数是:( )
A.1B.2C.3D.4
2.(2023·高一课时练习)如图所示,已知AD,BE分别为的边 BC,AC 上的中线,=,=,则( )
A.+B.+C.-D. +
3.(2023·安徽滁州·高一统考期末)如图,在平面四边形中,E,F分别为和的中点,那么( )
A.B.
C.D.
4.(2022·广东深圳·高一红岭中学校考期中)已知,则共线的三点为( )
A.B.C.D.
5.(2023·河南信阳·高一信阳高中校考阶段练习)在平行四边形中,与交于点,点满足,若,则( )
A.B.C.D.
6.(2023·江苏南通·高一统考阶段练习)已知P为平行四边形ABCD内一点,且,若,,则( )
A.B.1C.D.2
7.(2023·江苏南通·高一统考期中)已知,是两个不共线的向量,向量,.若,则( )
A.-2B.C.2D.
8.(2023·江苏·高一专题练习)已知O是平面上的一个定点,A、B、C是平面上不共线的三点,动点P满足,则点P的轨迹一定经过的( )
A.重心B.外心C.内心D.垂心
二、多选题
9.(2023·安徽淮北·高一淮北师范大学附属实验中学校考阶段练习)下列运算正确的是( )
A.B.
C.D.
10.(2023·陕西西安·高一期中)下列命题正确的的有( )
A.
B.
C.若,则共线
D.,则共线
11.(2023·浙江嘉兴·高一校考期中)如图,点是线段的三等分点,则下列结论正确的有( )
A.B.
C.D.
12.(2023·黑龙江齐齐哈尔·高一齐齐哈尔中学校考期中)如图在中,AD、BE、CF分别是边BC、CA、AB上的中线,且相交于点G,则下列结论正确的是( )
A.B.
C.D.
三、填空题
13.(2023·内蒙古呼伦贝尔·高二校考阶段练习)若,则 .
14.(2023·河北石家庄·高一校考期中)设是内部一点,且,则 .
15.(2023·黑龙江·高一富锦市第一中学校考阶段练习)如图所示,在正方形ABCD中,点E为BC的中点,点F为CD上靠近点C的四等分点,点G为AE上靠近点A的三等分点,则向量用与表示为
16.(2023·云南玉溪·高二玉溪第三中学校考期末)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成).类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设,若,则的值为 .
四、解答题
17.(2023·海南儋州·高一校考阶段练习)化简:
(1);
(2);
(3).
18.(2023·全国·高一课时练习)判断下列各小题中的向量,是否共线:
(1),;
(2),(其中两个非零向量和不共线);
(3),.
19.(2023·全国·高一随堂练习)如图,在中,,,点O是AC与BD的交点,点G是DO的中点,试用,表示.
20.(2023·河南南阳·高一社旗县第一高级中学校联考期末)如图,在中,.
(1)用,表示,;
(2)若点满足,证明:,,三点共线.
21.(2023·辽宁辽阳·高一统考期末)如图,在平行四边形中,,分别为,的中点.
(1)试问与是相等向量还是相反向量?说明你的理由.
(2)若,试用,表示,.
22.(2023·全国·高一随堂练习)如图,点D是中BC边的中点,,.
(1)试用,表示;
(2)若点G是的重心,能否用,表示?
(3)若点G是的重心,求.
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题06向量坐标表示与应用10大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题06向量坐标表示与应用10大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。