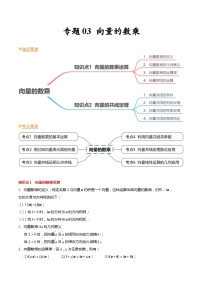
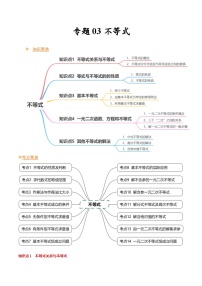
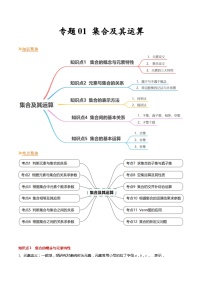
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04++向量的数量积（8大考点，知识串讲+热考题型+专题训练）-讲义

这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04++向量的数量积（8大考点，知识串讲+热考题型+专题训练）-讲义，文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题04向量的数量积8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题04向量的数量积8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。

知识聚焦
考点聚焦
知识点一、向量的数量积
1、向量的夹角
（1）定义：已知两个非零向量，，是平面上的任意一点，作，，
则（）叫做向量与的夹角．
（2）性质：当时，与同向；当时，与反向．
（3）向量垂直：如果与的夹角是，我们说与垂直，记作．
2、向量数量积的定义
（1）定义：非零向量与，它们的夹角为，数量叫做向量与的数量积(或内积)；
（2）记法：向量与的数量积记作，即；
零向量与任一向量的数量积为0；
3、投影向量
（1）设，是两个非零向量，，，
考虑如下变换：过的起点A和终点B，分别作所在直线的垂线，垂足分别为，，得到，我们称上述变换为向量向向量投影，叫做向量在向量上的投影向量．
（2）在平面内任取一点O，作，，过点M作直线的垂线，垂足为，则就是向量在向量上的投影向量，且．
（3）几何意义：数量积等于的长度||与在的方向上的投影的乘积。
4、向量数量积的物理背景
如果一个物体在力的作用下产生位移，那么力所做的功就等于力与位移的数量积，即，其中是与的夹角。
知识点二、向量数量积的性质与运算律
1、向量数量积的性质
设，都是非零向量，是单位向量，θ为与(或)的夹角．则
（1）；
（2）；
（3）当与同向时，；当与反向时，；
特别地，或；
（4）cs θ＝；
（5）
2、向量数量积满足的运算律
（1）；
（3）(λ为实数)；
（3）；
（4）两个向量，的夹角为锐角⇔且，不共线；
两个向量，的夹角为钝角⇔且，不共线．
（5）平面向量数量积运算的常用公式

知识点三、求平面向量数量积的方法
1、定义法：若已知向量的模及夹角，则直接利用公式，运用此法计算数量积的关键是正确确定两个向量的夹角，条件是两向量的始点必须重合，否则，要通过平移使两向量符合以上条件；
2、运算律转化法：由可得如下运算公式：；；；
3、向量的线性运算转化法：涉及平面图形中向量的数量积的计算时，要结合向量的线性运算，将未知向量转化为已知向量求解。
考点剖析
考点1 向量数量积的概念辨析
【例1】（2023·高一单元测试）以下关于两个非零向量的数量积的叙述中，错误的是（ ）
A．两个向量同向共线，则他们的数量积是正的
B．两个向量反向共线，则他们的数量积是负的
C．两个向量的数量积是负的，则他们夹角为钝角
D．两个向量的数量积是0，则他们互相垂直
【变式1-1】（2023·上海闵行·高一统考期末）下列命题中正确的是（ ）
A． B． C．若，则 D．若，则
【变式1-2】（2023·陕西咸阳·高一校考阶段练习）在等式①；②；③；④若，且，则；其中正确的命题的个数为（ ）
A．1 B．2 C．3 D．4
【变式1-3】（2023·全国·高一课时练习）（多选）下列说法正确的是（ ）
A．对任意向量，都有
B．若且，则
C．对任意向量，都有
D．对任意向量，都有
考点2 向量数量积的运算
【例2】（2023·河南·高一校考阶段练习）在边长为2的等边中，的值是（ ）
A．4 B． C．2 D．
【变式2-1】（2023·全国·高一课时练习）已知向量、满足，，且与夹角的余弦值为，则（ ）
A． B． C． D．12
【变式2-2】（2023·全国·高一课时练习）已知向量，向量与的夹角都是，且，试求
（1）；
（2）．
【变式2-3】（2023·湖北荆州·高一沙市中学校考期中）已知边长为1的菱形中，角，则 .
【变式2-4】（2023·安徽马鞍山·高一当涂第一中学校考期中）如图，在中，为线段上一点，若，，且与的夹角为，则的值为 .
考点3 利用数量积求向量模长
【例3】（2023·天津和平·高一统考期末）已知平面向量，且与的夹角为，则（ ）
A．12 B．16 C． D．
【变式3-1】（2023·江苏·高一课时练习）已知平面向量，满足，，与的夹角为，则的值为 .
【变式3-2】（2023·全国·高一课时练习）若平面向量两两的夹角相等，且，则（ ）
A．2 B．5 C．2或5 D．或
【变式3-3】（2023·河南·高一济源市第四中学校考阶段练习）已知向量，满足，，，则 ．
【变式3-4】（2023·广东佛山·高一校考阶段练习）设点、、、为四个互不相同的点，且在同一圆周上，若，且，则 .
考点4 利用数量积求向量夹角
【例4】（2023·新疆乌鲁木齐·高一校考期中）已知向量，，，则向量与的夹角大小为（ ）
A． B． C． D．
【变式4-1】（2023·全国·高一随堂练习）若，，且，则与的夹角为 ；
【变式4-2】（2023·湖南常德·高一阶段练习）已知是夹角为的两个单位向量，设向量，，则与的夹角为（ ）
A． B． C． D．
【变式4-3】（2023·全国·高一课时练习）已知单位向量，满足，若向量，则 ．
【变式4-4】（2023·江苏连云港·高一统考期中）在任意四边形中，点，分别在线段，上，且，，，，，则与夹角的余弦值为（ ）
A． B． C． D．
考点5 两个向量的垂直问题
【例5】（2023·高一单元测试）（多选）是边长为2的等边三角形，已知向量满足，，则下列结论不正确的是（ ）
A． B． C． D．
【变式5-1】（2023·全国·高一随堂练习）若向量，满足，且，，则（ ）．
A．2 B． C．1 D．
【变式5-2】（2023·辽宁铁岭·高一西丰县高级中学校考期中）已知非零向量满足，则与的夹角为 .
【变式5-3】（2023·河南新乡·高一校考阶段练习）已知单位向量，的夹角为，，，若，则实数 .
【变式5-4】（2023·山西朔州·高一校考阶段练习）已知，，与的夹角为45°，要使与垂直，则的值为（ ）
A． B． C． D．
考点6 投影及投影向量
【例6】（2023·全国·高一课时练习）已知向量与的夹角为，，则向量在上的投影向量为（ ）
A． B． C． D．
【变式6-1】（2023·湖北·高一仙桃中学校考阶段练习）已知为单位向量，，向量，的夹角为，则在上的投影向量是（ ）
A． B． C． D．
【变式6-2】（2023·云南昆明·高一校考阶段练习）已知非零向量满足，，则在方向上的投影向量的模为 ．
【变式6-3】（2023·河南新乡·高一校考阶段练习）设单位向量､的夹角为，，，则在方向上的投影为（ ）
A． B． C． D．
考点7 由数量积判断三角形形状
【例7】（2023·河北石家庄·高一校考期中）在中，若，则的形状是（ ）
A．等边三角形 B．直角三角形 C．等腰三角形 D．等腰直角三角形
【变式7-1】（2023·山东菏泽·高一鄄城县第一中学校考阶段练习）在中，，则的形状是（ ）
A．锐角三角形 B．钝角三角形 C．直角三角形 D．不能确定
【变式7-2】（2023·贵州黔西·高一校考阶段练习）若O是所在平面内一点，且满足，则的形状是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等边三角形
【变式7-3】（2023·上海浦东新·高一校考阶段练习）在中，若，则的形状是 .
考点8 求向量数量积的最值
【例8】（2023·山东青岛·高一统考期中）已知点是边长为2的正的内部（不包括边界）的一个点，则的取值范围为（ ）
A． B． C． D．
【变式8-1】（2023·河南省直辖县级单位·高一济源市第四中学校考阶段练习）中，，，，点C是线段上的动点，点D是的中点，则的最小值为（ ）
A． B． C． D．2
【变式8-2】（2023·北京顺义·高一牛栏山一中校考期中）如图，边长为2的菱形的对角线相交于点，点在线段上运动，若，则的最小值为 .
【变式8-3】（2023·安徽池州·高一校联考期中）已知菱形的边长为1，，点E是边上的动点，则的最大值为（ ）．
A．1 B． C． D．
过关检测
一、单选题
1．（2023·高一单元测试）已知向量，满足，且与的夹角为，则（ ）
A．6 B．8 C．10 D．14
2．（2023·甘肃临夏·高一统考期末）在中，，，，则（ ）
A． B．16 C． D．9
3．（2023·新疆喀什·高一统考期末）已知平面向量，满足，，，则与的夹角为（ ）
A． B． C． D．
4．（2023·宁夏吴忠·高一吴忠中学校考期末）若，是夹角为的两个单位向量，且与的夹角为（ ）
A． B． C． D．
5．（2023·山东菏泽·高一东明县第一中学校考阶段练习）若平面向量，，，两两的夹角相等，且，，，则（ ）．
A．2 B．4或 C．5 D．2或5
6．（2023·吉林·高一榆树市实验高级中学校校联考期末）如图，已知，，，任意点关于点的对称点为，点关于点的对称点为，则（ ）
A．1 B．2 C． D．
7．（2023·河南·高一济源市第四中学校考阶段练习）若向量与向量的夹角为，且，则向量在向量方向上的投影向量是（ ）
A． B． C． D．
8．（2023·北京海淀·高一清华附中校考期末）已知，，，则的最大值为（ ）
A．1 B．2 C． D．4
二、多选题
9．（2023·贵州贵阳·高一校考阶段练习）如果是两个单位向量，那么下列四个结论中不正确的是（ ）
A． B． C． D．
10．（2023·云南保山·高一统考期中）已知矩形的面积为，则（ ）
A．5 B．3 C． D．
11．（2023·河北石家庄·高一校考期中）若向量满足，，则（ ）
A． B．与的夹角为 C． D．在上的投影向量为
12．（2023·四川遂宁·高一射洪中学校考阶段练习）下列说法正确的有（ ）
A．
B．λ、μ为非零实数，若，则与共线
C．若，则
D．若平面内有四个点A、B、C、D，则必有
三、填空题
13．（2023·上海·高一校考期中）设向量满足，，则 ．
14．（2023·全国·高一课时练习）已知平面向量满足，则实数的值为 ．
15．（2023·山西朔州·高一校考阶段练习）已知与是两个单位向量，且向量与的夹角为，则向量在向量上的投影向量为 ．
16．（2023·山东菏泽·高一东明县第一中学校考阶段练习）如图，在中，已知，，，，边上的两条中线，相交于点，则的余弦值是 ．
四、解答题
17．（2023·全国·高一专题练习）已知向量，向量与，的夹角都是60°，且，，，试求
（1）；
（2）.
18．（2023·青海西宁·高一校考期中）设向量、满足，且．
（1）求与夹角的大小；
（2）求与夹角的大小．
19．（2023·全国·高一随堂练习）已知向量为向量的夹角.
（1）求的值；
（2）若，求实数的值.
20．（2023·山西朔州·高一校考阶段练习）已知，，．
（1）求的值；
（2）求向量与夹角的正切值．
21．（2023·贵州黔西·高一校考阶段练习）已知向量与的夹角为，且，，求：
（1）；
（2）在方向上的投影向量的模．
22．（2023·陕西西安·高一期中）已知向量满足，且的夹角为.
（1）求的模；
（2）若与互相垂直，求λ的值.