

【寒假作业】高中数学 高一寒假巩固提升训练 专题07+基本立体图形+(四大考点)-练习
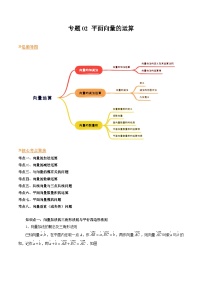
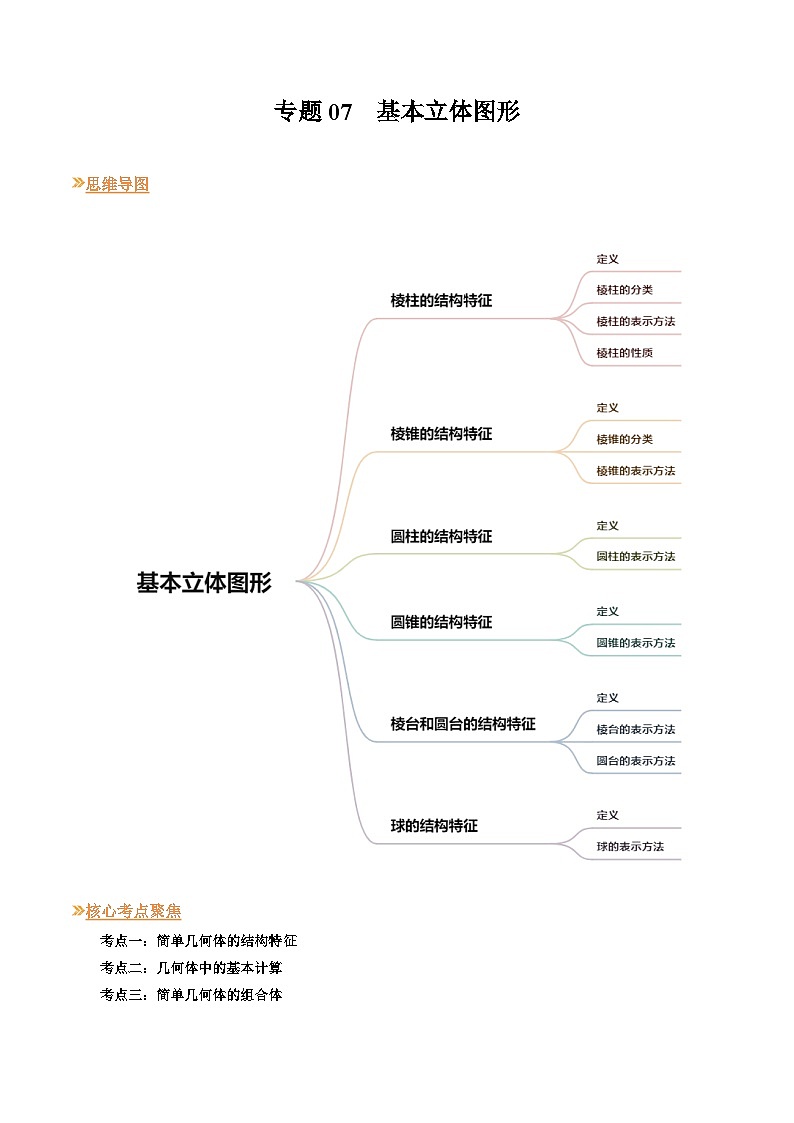
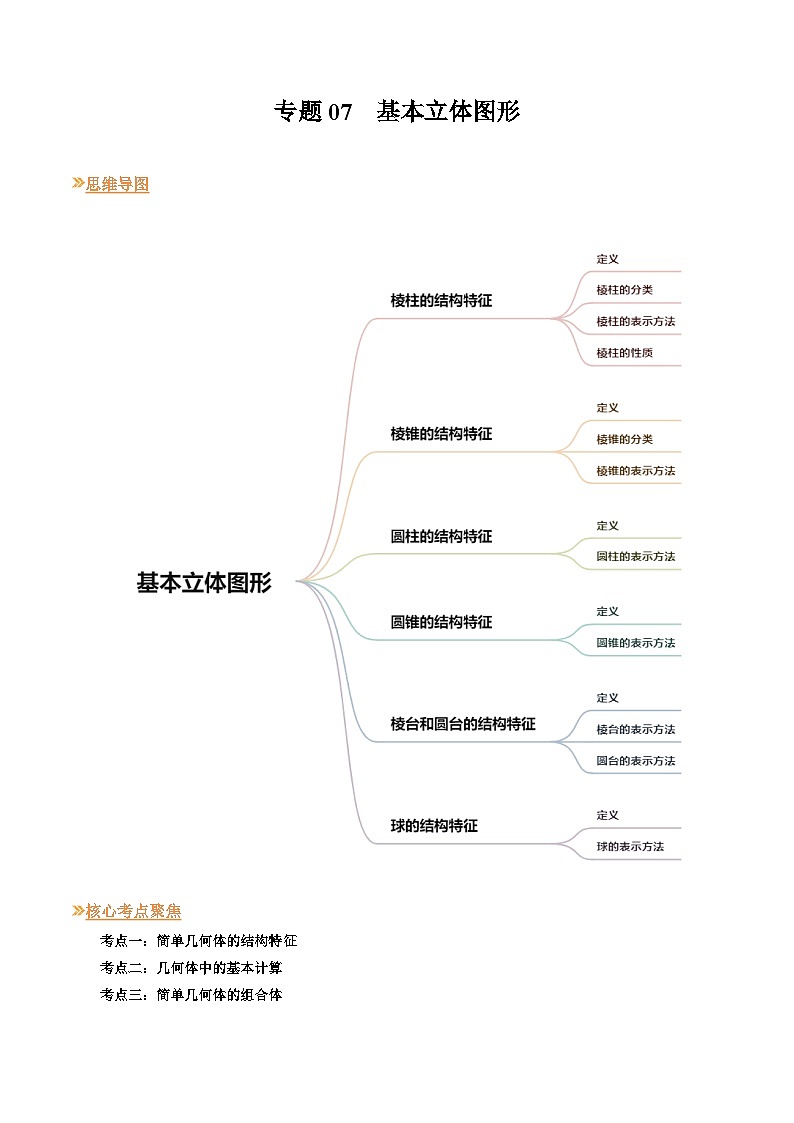
展开思维导图
核心考点聚焦
考点一:简单几何体的结构特征
考点二:几何体中的基本计算
考点三:简单几何体的组合体
考点四:简单几何体的表面展开与折叠问题
知识点一:棱柱的结构特征
1、定义:一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.在棱柱中,两个相互平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱.侧面与底的公共顶点叫做棱柱的顶点.棱柱中不在同一平面上的两个顶点的连线叫做棱柱的对角线.过不相邻的两条侧棱所形成的面叫做棱柱的对角面.
2、棱柱的分类:底面是三角形、四边形、五边形、……的棱柱分别叫做三棱柱、四棱柱、五棱柱……
3、棱柱的表示方法:
①用表示底面的各顶点的字母表示棱柱,如下图,四棱柱、五棱柱、六棱柱可分别表示为、、;
②用棱柱的对角线表示棱柱,如上图,四棱柱可以表示为棱柱或棱柱等;五棱柱可表示为棱柱、棱柱等;六棱柱可表示为棱柱、棱柱、棱柱等.
4、棱柱的性质:棱柱的侧棱相互平行.
知识点诠释:
有两个面互相平行,其余各个面都是平行四边形,这些面围成的几何体不一定是棱柱.如下图所示的几何体满足“有两个面互相平行,其余各个面都是平行四边形”这一条件,但它不是棱柱.
判定一个几何体是否是棱柱时,除了看它是否满足:“有两个面互相平行,其余各个面都是平行四边形”这两个条件外,还要看其余平行四边形中“每两个相邻的四边形的公共边都互相平行”即“侧棱互相平行”这一条件,不具备这一条件的几何体不是棱柱.
知识点二:棱锥的结构特征
1、定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.这个多边形面叫做棱锥的底面.有公共顶点的各个三角形叫做棱锥的侧面.各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
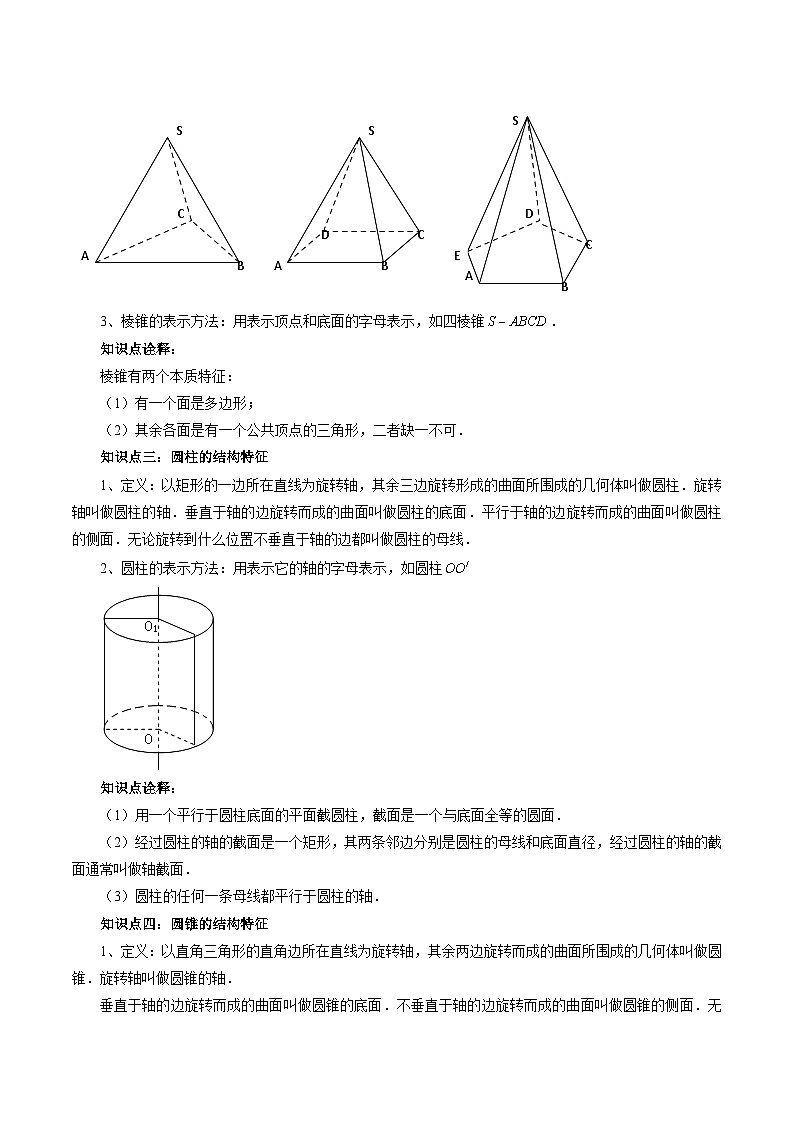
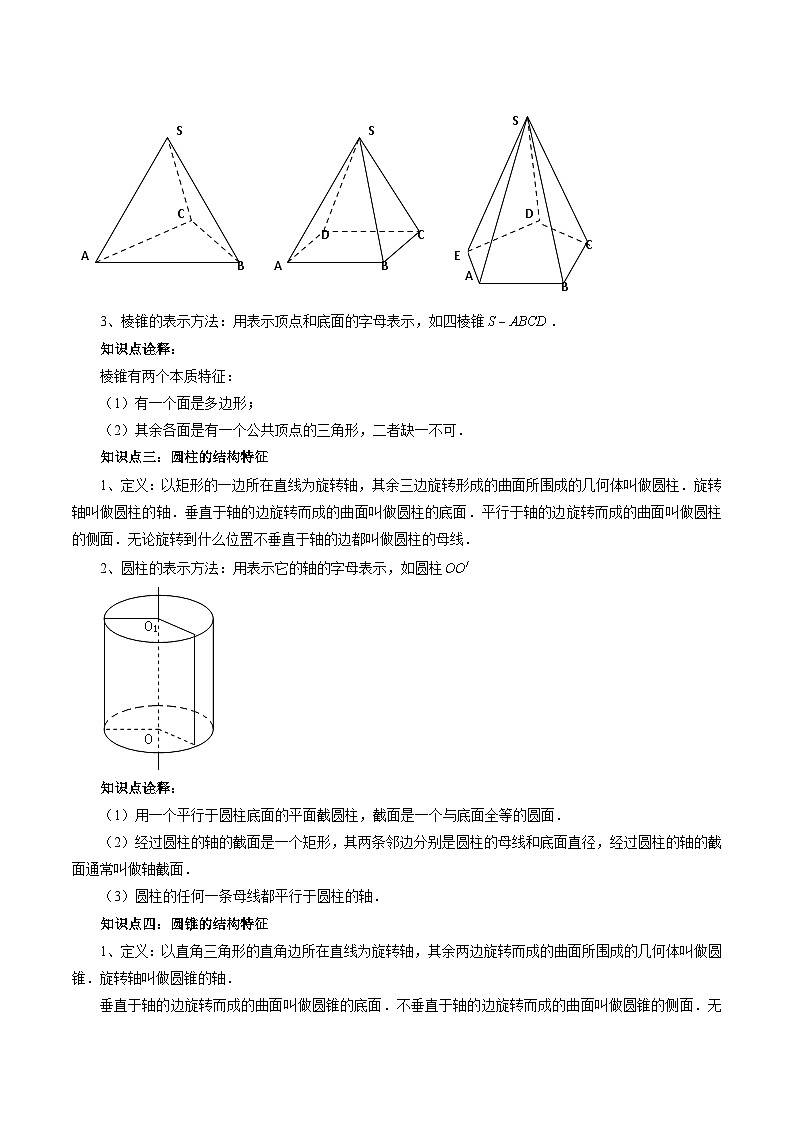
2、棱锥的分类:按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥……;S
S
D
D
C
C
B
B
A
A
E
C
B
A
S
3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥.
知识点诠释:
棱锥有两个本质特征:
(1)有一个面是多边形;
(2)其余各面是有一个公共顶点的三角形,二者缺一不可.
知识点三:圆柱的结构特征
1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴.垂直于轴的边旋转而成的曲面叫做圆柱的底面.平行于轴的边旋转而成的曲面叫做圆柱的侧面.无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线.
2、圆柱的表示方法:用表示它的轴的字母表示,如圆柱
知识点诠释:
(1)用一个平行于圆柱底面的平面截圆柱,截面是一个与底面全等的圆面.
(2)经过圆柱的轴的截面是一个矩形,其两条邻边分别是圆柱的母线和底面直径,经过圆柱的轴的截面通常叫做轴截面.
(3)圆柱的任何一条母线都平行于圆柱的轴.
知识点四:圆锥的结构特征
1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥.旋转轴叫做圆锥的轴.
垂直于轴的边旋转而成的曲面叫做圆锥的底面.不垂直于轴的边旋转而成的曲面叫做圆锥的侧面.无论旋转到什么位置不垂直于轴的边都叫做圆锥的母线.
2、圆锥的表示方法:用表示它的轴的字母表示,如圆锥.
知识点诠释:
(1)用一个平行于圆锥底面的平面去截圆锥,截面是一个比底面小的圆面.
(2)经过圆锥的轴的截面是一个等腰三角形,其底边是圆锥底面的直径,两腰是圆锥侧面的两条母线.
(3)圆锥底面圆周上任意一点与圆锥顶点的连线都是圆锥侧面的母线.
知识点五:棱台和圆台的结构特征
1、定义:用一个平行于棱锥(圆锥)底面的平面去截棱锥(圆锥),底面和截面之间的部分叫做棱台(圆台);原棱锥(圆锥)的底面和截面分别叫做棱台(圆台)的下底面和上底面;原棱锥(圆锥)的侧面被截去后剩余的曲面叫做棱台(圆台)的侧面;原棱锥的侧棱被平面截去后剩余的部分叫做棱台的侧棱;原圆锥的母线被平面截去后剩余的部分叫做圆台的母线;棱台的侧面与底面的公共顶点叫做棱台的顶点;圆台可以看做由直角梯形绕直角边旋转而成,因此旋转的轴叫做圆台的轴.
2、棱台的表示方法:用各顶点表示,如四棱台;
3、圆台的表示方法:用表示轴的字母表示,如圆台;
知识点诠释:
(1)棱台必须是由棱锥用平行于底面的平面截得的几何体.所以,棱台可还原为棱锥,即延长棱台的所有侧棱,它们必相交于同一点.
(2)棱台的上、下底面是相似的多边形,它们的面积之比等于截去的小棱锥的高与原棱锥的高之比的平方.
(3)圆台可以看做由圆锥截得,也可以看做是由直角梯形绕其直角边旋转而成.
(4)圆台的上、下底面的面积比等于截去的小圆锥的高与原圆锥的高之比的平方.
知识点六:球的结构特征
1、定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球.半圆的半径叫做球的半径.半圆的圆心叫做球心.半圆的直径叫做球的直径.
2、球的表示方法:用表示球心的字母表示,如球O.
知识点诠释:
(1)用一个平面去截一个球,截面是一个圆面.如果截面经过球心,则截面圆的半径等于球的半径;如果截面不经过球心,则截面圆的半径小于球的半径.
(2)若半径为的球的一个截面圆半径为,球心与截面圆的圆心的距离为,则有.
知识点七:特殊的棱柱、棱锥、棱台
特殊的棱柱:侧棱不垂直于底面的棱柱称为斜棱柱;垂直于底面的棱柱称为直棱柱;底面是正多边形的直棱柱是正棱柱;底面是矩形的直棱柱叫做长方体;棱长都相等的长方体叫做正方体;
特殊的棱锥:如果棱锥的底面是正多边形,且各侧面是全等的等腰三角形,那么这样的棱锥称为正棱锥;侧棱长等于底面边长的正三棱锥又称为正四面体;
特殊的棱台:由正棱锥截得的棱台叫做正棱台;
知识点八:简单组合体的结构特征
1、组合体的基本形式:①由简单几何体拼接而成的简单组合体;②由简单几何体截去或挖去一部分而成的几何体;
2、常见的组合体有三种:①多面体与多面体的组合;②多面体与旋转体的组合;③旋转体与旋转体的组合.
①多面体与多面体的组合体
由两个或两个以上的多面体组成的几何体称为多面体与多面体的组合体.如下图(1)是一个四棱柱与一个三棱柱的组合体;如图(2)是一个四棱柱与一个四棱锥的组合体;如图(3)是一个三棱柱与一个三棱台的组合体.
②多面体与旋转体的组合体
由一个多面体与一个旋转体组合而成的几何体称为多面体与旋转体的组合体如图(1)是一个三棱柱与一个圆柱组合而成的;如图(2)是一个圆锥与一个四棱柱组合而成的;而图(3)是一个球与一个三棱锥组合而成的.
③旋转体与旋转体的组合体
由两个或两个以上的旋转体组合而成的几何体称为旋转体与旋转体的组合体.如图(1)是由一个球体和一个圆柱体组合而成的;如图(2)是由一个圆台和两个圆柱组合而成的;如图(3)是由一个圆台、一个圆柱和一个圆锥组合而成的.
几何体中的计算问题
几何体的有关计算中要注意下列方法与技巧:
(1)在正棱锥中,要掌握正棱锥的高、侧面、等腰三角形中的斜高及高与侧棱所构成的两个直角三角形,有关证明及运算往往与两者相关.
(2)正四棱台中要掌握其对角面与侧面两个等腰梯形中关于上、下底及梯形高的计算,有关问题往往要转化到这两个等腰梯形中.另外要能够将正四棱台、正三棱台中的高与其斜高、侧棱在合适的平面图形中联系起来.
(3)研究圆柱、圆锥、圆台等问题的主要方法是研究它们的轴截面,这是因为在轴截面中,易找到所需有关元素之间的位置、数量关系.
(4)圆柱、圆锥、圆台的侧面展开是把立体几何问题转化为平面几何问题处理的重要手段之一.
(5)圆台问题有时需要还原为圆锥问题来解决.
(6)关于球的问题中的计算,常作球的一个大圆,化“球”为“圆”,应用平面几何的有关知识解决;关于球与多面体的切接问题,要恰当地选取截面,化“空间”为平面.
考点剖析
考点一:简单几何体的结构特征
例1.(2024·甘肃酒泉·高二校考期末)下列描述中,不是棱锥几何结构特征的是( )
A.三棱锥有4个面是三角形B.棱锥的侧面都是三角形
C.棱锥都有两个互相平行的多边形面D.棱锥的侧棱交于一点.
【答案】C
【解析】A中,根据棱锥的几何结构,可得三棱锥有4个面是三角形 ,所以A正确;
B中,根据棱锥的定义,可得棱锥的侧面都是三角形,所以B正确;
C中,根据棱锥的定义,可得棱锥都没有两个互相平行的多边形面,所以C错误;
D中,根据棱锥的定义,可得棱锥的侧棱交于一点,所以D正确.
故选:C.
例2.(2024·宁夏吴忠·高一统考期末)下列关于几何体特征的判断正确的是( )
A.一个斜棱柱的侧面不可能是矩形
B.底面是正多边形的棱锥一定是正棱锥
C.有一个面是边形的棱锥一定是棱锥
D.平行六面体的三组对面中,必有一组是全等的矩形
【答案】C
【解析】对于A中,斜棱柱的侧面中,可以有的侧面是矩形,所以A不正确;
对于B中,根据正棱锥的定义,底面是正多边形且顶点在底面的射影为底面多边形的中心的棱锥是正棱锥,所以B不正确;
对于C中,根据棱锥的分类,可得有一个面是边形的棱锥一定是棱锥,所以C正确;
对于D中,平行六面体的三组对面中,必有一组是全等的平行四边形,所以D错误.
故选:C.
例3.(2024·全国·高一随堂练习)下列命题正确的是( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.有一个面是多边形,其余各面是三角形的几何体是棱锥
C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体是棱台
【答案】C
【解析】对于A,有两个面平行,其余各面都是四边形的几何体不一定是棱柱,可能是棱台或组合图形,故A错误;
对于B,有一个面是多边形,其余各面是有公共顶点的三角形的几何体才是棱锥,故B错误;
对于C,根据棱柱的定义,有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱,故C正确;
对于D,用一个平行于底面的平面去截棱锥,底面与截面之间的部分组成的几何体才是棱台,故D错误.
故选:C.
变式1.(2024·山西太原·高一校考阶段练习)下列命题中正确的是( )
A.两个底面平行且相似,其余各面是梯形的多面体是棱台
B.三棱柱的侧面为三角形
C.棱台的各侧棱延长后不一定交于一点
D.棱锥的侧面和底面可以都是三角形
【答案】D
【解析】棱台的侧面梯形的腰(即棱台的侧棱)的延长线都相交于一点,C错误;
而选项A中侧面梯形的腰不一定交于一点,A错误;
棱柱的各侧面都是平行四边形,B错误;
棱锥的侧面都是三角形,底面可以是三角形,如三棱锥,D正确.
故选:D
变式2.(2024·山西朔州·高一校联考阶段练习)下列几何体中,棱数最多的是( )
A.五棱锥B.三棱台
C.三棱柱D.四棱锥
【答案】A
【解析】因为五棱锥有10条棱,三棱台有9条棱,三棱柱有9条棱,四棱锥有8条棱,
所以这些几何体中棱数最多的是五棱锥,
故选:A
考点二:几何体中的基本计算
例4.(2024·高一课时练习)长方体的同一顶点处的相邻三个面的面积分别为12,6,8,则长方体的体对角线长为 .
【答案】
【解析】
设长方体从顶点B出发的三条棱长分别为,且,,,则,,,
所以长方体中线段的长等于.
故答案为:
例5.(2024·高一课时练习)圆柱的母线长为5,底面半径为2,称过圆柱的轴的任意平面与圆柱形成的平面为轴截面,则该圆柱轴截面面积为 .
【答案】20
【解析】轴截面为矩形,两边长分别为5和4,故轴截面的面积为.
故答案为:20
例6.(2024·高一课时练习)用一个平行于圆锥底面的平面截这个圆锥,截得的两个几何体分别为一个小圆锥和一个圆台,若小圆锥的底面面积与原圆锥的底面面积之比为1:4,圆台的母线长为9 cm,则原来的圆锥的母线长为 .
【答案】18 cm
【解析】设轴截面如图所示,由已知得圆 与圆的面积比为 ,所以半径比 ,进而得,所以是的中点,且,故 ,
故答案为:18 cm
变式3.(2024·高一课时练习)长、宽、高分别为3、4,5的两个相同的长方体,把它们某两个全等的面重合在一起,组成大长方体,则大长方体对角线最长为 .
【答案】
【解析】当大长方体的长、宽、高分别为、、时,
体对角线为.
当大长方体的长、宽、高分别为、、时,
体对角线为.
当大长方体的长、宽、高分别为、、时,
体对角线为.
因为,所以大长方体对角线最长为.
故答案为:
考点三:简单几何体的组合体
例7.(2024·高一课时练习)已知,ABCD为等腰梯形,两底边为AB,CD且,梯形ABCD绕AB所在的直线旋转一周所得的几何体是由 、 、 的几何体构成的组合体.
【答案】 圆锥 圆柱 圆锥
【解析】如图所示:作于,于,
绕所在的直线旋转一周得到圆锥;
矩形绕所在的直线旋转一周得到圆柱;
绕所在的直线旋转一周得到圆锥;
故答案为:圆锥;圆柱;圆锥;
例8.(2024·全国·高一专题练习)如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是 .
【答案】①⑤
【解析】一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形去掉上侧一条边,而圆锥的轮廓是三角形除去一条边或抛物线的一部分,且三角形顶点必在矩形下侧底边中点上、抛物线顶点不可能在矩形下侧底边上.
故答案为:①⑤
例9.(2024·高一课时练习)如图所示的几何体,关于其结构特征,下列说法不正确的是 .
①该几何体是由两个同底的四棱锥组成的几何体;
②该几何体有12条棱、6个顶点;
③该几何体有8个面,并且各面均为三角形;
④该几何体有9个面,其中一个面是四边形,其余均为三角形.
【答案】④
【解析】平面ABCD可将该几何体分割成两个四棱锥,因此该几何体是这两个四棱锥的组合体,因而四边形ABCD是它的一个截面,而不是一个面.
故答案为:④.
考点四:简单几何体的表面展开与折叠问题
例10.(2024·山东聊城·高一山东聊城一中校考)如图,直三棱柱中,,,为线段上的一个动点,则的最小值是 .
【答案】
【解析】将图中的和放置于同一平面内,如图所示,
则.
因为直三棱柱中,,,
所以中,.
同理,在中,,所以
所以在图中,,
所以,即.
所以的最小值是.
故答案为:.
例11.(2024·吉林四平·高一校考阶段练习)如图正三棱柱的底面边长为,高为2,一只蚂蚁要从顶点沿三棱柱的表面爬到顶点,若侧面紧贴墙面(不能通行),则爬行的最短路程是 .
【答案】
【解析】正三棱柱的侧面部分展开图如图所示,
图1,连接与交于点,则爬行的最短路程时沿着爬行,
此时,
图2,连接,过作AB的垂线交于点,则,
则,所以,
∵,∴爬行的最短路程是.
故答案为:.
例12.(2024·浙江宁波·高一校联考)已知正方体的棱长为,一蚂蚁沿着正方体的表面从点爬到点的最短距离是 .
【答案】
【解析】
如图所示,将正方体的侧面与展开,
则最短距离为,
故答案为:.
变式4.(2024·山东菏泽·高一山东省东明县第一中学校考阶段练习)正三棱锥中,,过点A作一截面与侧棱分别交于点,,则截面周长的最小值为 .
【答案】
【解析】将三棱锥的侧面沿,,剪开,得到如图所示的五边形,
连接,分别交,于,,再将展开图围成三棱锥的侧面,得到,
即为周长最小的截面三角形,由此可得截面周长的最小值等于线段的长.
正三棱锥中,,所以,
又,所以等腰中,,即截面周长的最小值为.
故答案为:.
变式5.(2024·高一单元测试)如图,已知圆柱的高为h,底面半径为,轴截面为矩形,在母线上有一点,且,在母线上取一点,使,则圆柱侧面上P、Q两点的最短距离为 .
【答案】
【解析】如图,把圆柱的半个侧面展开,是一个下长为,宽为的矩形,
,,过作,为垂足,所以,
即可把放在一个直角边为和的直角三角形中,
根据勾股定理可得:.
故答案为:.
变式6.(2024·福建三明·高一校联考)圆锥的母线,高为,点是的中点,一质点自点出发,沿侧面绕行一周到达点的最短路程为 .
【答案】
【解析】将圆锥的侧面展开,连接,
则的长即为质点绕行的最短路程,由题设易知:圆锥底面半径为2;
在中,,,弧长,;
利用余弦定理得:,;
质点自点出发,沿侧面绕行一周到达点的最短路程为.
故答案为:.
过关检测
一、单选题
1.(2024·河北石家庄·高一石家庄二十三中校考)下列说法正确的有( )
A.有两个面互相平行,其余各面均是平行四边形的多面体是棱柱
B.用任意一个平面去截球得到的截面一定是一个圆面
C.侧面是全等的矩形的五棱柱一定是正五棱柱
D.过圆锥顶点的所有截面中,轴截面面积最大
【答案】B
【解析】如下图的多面体,有两个面互相平行,其余各面均是平行四边形的,但它不是棱柱,A错;
用任意一个平面去截球得到的截面一定是一个圆面,B正确;
侧面是全等的矩形的五棱柱的底面不一定是正五边形,C错;
过圆锥顶点的所有截面中,设两条母线的平角为,母线长为,则截面面积为,
当轴截面等腰三角形的顶角大于,截面中两条母线夹角为的截面面积最大,D错.
故选:B.
2.(2024·河南省直辖县级单位·高一河南省济源第一中学校考阶段练习)一个正棱锥被平行于底面的平面所截,若截得的截面面积与底面面积的比为1∶2,则此正棱锥的高被分成的两段之比为( )
A.1∶B.1∶4C.1∶(+1)D.1∶(﹣1)
【答案】D
【解析】设截后棱锥的高为h,原棱锥的高为H,
由于截面与底面相似,一个正棱锥被平行于底面的平面所截,
若截得的截面面积与底面面积的比为1∶2,,
则此正棱锥的高被分成的两段之比:.
故选:D
3.(2024·河北邢台·高一河北南宫中学校考阶段练习)下列说法正确的是( )
A.多面体至少有5个面
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.六棱柱有6条侧棱,6个侧面,侧面均为平行四边形
【答案】D
【解析】对于A,一个多面体至少有4个面,如三棱锥有4个面,故A错误;
对于B,因为不能保证各侧棱的延长线交于一点,故B错误;
对于C,反例如下图,上、下底面是全等的菱形,各侧面是全等的正方形,它不是正方体;故C错误;
对于D,根据棱柱的定义,知选项D正确.
故选:D
4.(2024·广东东莞·高一东莞市东莞中学松山湖学校校考阶段练习)下列命题正确的是( )
A.用一个平面去截圆锥,得到一个圆锥和一个圆台
B.棱柱的侧棱都相等,侧面都是全等的平行四边形
C.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都可以构成直角三角形
D.一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台
【答案】C
【解析】只有在平面平行于圆锥底面时,才能将圆锥截为一个圆锥和一个圆台,
当平面不平行于圆锥底面时,得到的几何体并非圆锥和圆台,所以A错;
棱柱的侧棱都相等且平行,且侧面是平行四边形,
但其底面多边形各边不一定相等,则侧面并不一定全等,所以B错;
圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都可以构成直角三角形,所以C对;
直角梯形绕下底所在直线旋转一周,所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,
如图所示,所以D错.
故选:C.
5.(2024·河南郑州·高一校联考)如图,正三棱锥中,,侧棱长为,一只虫子从A点出发,绕三棱锥的三个侧面爬行一周后,又回到A点,则虫子爬行的最短距离是( )
A.B.C.D.
【答案】B
【解析】将正三棱锥沿剪开,得到侧面展开图,如图所示,
因为,即,
由的周长为,
要使的周长的最小,则共线,即,
又由正三棱锥侧棱长为,是等边三角形,
所以,即虫子爬行的最短距离是.
故选:B.
6.(2024·辽宁锦州·高一渤海大学附属高级中学校考阶段练习)某同学为表达对“新冠疫情”抗疫一线医护人员的感激之情,亲手为他们制作了一份礼物,用正方体纸盒包装,并在正方体六个面上分别写了“致敬最美逆行”六个字,该正方体纸盒水平放置的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如图是该正方体的展开图.若图中“行”在正方体的左面,那么在正方体右面的字是( )
A.最B.美C.逆D.敬
【答案】A
【解析】把正方体的表面展开图再折成正方体,如图,“行”在正方体的左面,那么在正方体右面的字是“最”.
故选:A.
7.(2024·陕西宝鸡·高一宝鸡中学校考阶段练习)已知圆锥的底面半径为2,侧面展开图为圆心角为的扇形,则该圆锥的高为( )
A.6B.C.4D.3
【答案】B
【解析】设圆锥的母线长为,
圆锥的底面半径,侧面展开图的圆心角为,
,可得母线长,
圆锥的高.
故选:B
8.(2024·山东泰安·高一泰安一中校考)某景区为提升游客观赏体验,搭建一批圆锥形屋顶的小屋(如图1).现测量其中一个屋顶,得到圆锥的底面直径长为,母线长为(如图2).若是母线的一个三等分点(靠近点S),从点A到点绕屋顶侧面一周安装灯光带,则灯光带的最小长度为( )
A.B.C.D.
【答案】C
【解析】将圆锥侧面沿母线展开,其侧面展开图为如图所示的扇形,则的长度即为灯光带的最小长度,
,,
在中,,,
,
解得:,即灯光带的最小长度为.
故选:C.
二、多选题
9.(2024·吉林长春·高一长春外国语学校校考)下列说法正确的是( )
A.棱台的侧面都是等腰梯形
B.棱柱的侧棱长都相等,但侧棱不一定都垂直于底面
C.底面半径为r,母线长为2r的圆锥的轴截面为等边三角形
D.以三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥
【答案】BC
【解析】A. 棱台的侧棱延长后交于一点,但侧面不一定是等腰梯形,如一条侧棱垂直于底面,那么会有两个侧面为直角梯形,故错误;
B.棱柱的侧棱长都相等,但侧棱不一定都垂直于底面,故正确;
C.底面半径为r,母线长为2r的圆锥的轴截面为等边三角形,故正确;
D.当以直角三角形的直角边所在直线为轴旋转一周所得的旋转体是圆锥,以直角三角形的斜边所在直线为轴旋转一周所得的旋转体是两个同底的圆锥,故错误;
故选:BC
10.(2024·新疆·高一兵团第三师第一中学校考阶段练习)长方体的棱长,则从点沿长方体表面到达点的距离可以为( )
A.B.C.D.
【答案】ABC
【解析】从点沿长方体表面到达有三种展开方式,
若以为轴展开,
则;
以为轴展开,
则,
以为轴展开,
.
故选:ABC.
11.(2024·山西大同·高一校考阶段练习)下列命题中不正确的是( )
A.圆柱、圆锥、圆台的底面都是圆面
B.正四棱锥的侧面都是正三角形
C.用一个平面去截圆锥,截面与底面之间的部分是圆台
D.平行六面体的每个面都是平行四边形
【答案】BC
【解析】对于A,圆柱、圆锥、圆台的底面都是圆面,故选项A正确;
对于B,正四棱锥的侧面都是等腰三角形,不一定是正三角形,故选项B错误;
对于C,用平行于圆锥底面的平面去截圆锥,截面与底面之间的部分是圆台,而不是用一个平面去截圆锥,故选项C错误,
对于D,平行六面体的每个面都是平行四边形,故选项D正确,
故选:BC.
12.(2024·北京·高三校考强基计划)在直三棱柱中,,点P在线段上,则的( )
A.最小值为B.最小值为
C.最大值为D.最大值为
【答案】BD
【解析】如图展开,其中是斜边为的等腰直角三角形,
是斜边为6的等腰直角三角形.
当三点共线时,取得最小值.
当P位于C点位置时,取得最大值.
故选:BD.
三、填空题
13.(2024·云南红河·高一校考开学考试)若一个圆锥的底面圆半径为2,其侧面展开图的圆心角为,则圆锥的母线长是 .
【答案】6
【解析】设圆锥的母线长为l,根据题意得,解得,
即圆锥的母线长为6.
故答案为:6.
14.(2024·全国·高一随堂练习)一个几何体由7个面围成,其中两个面是互相平行且全等的五边形,其他各面都是全等的矩形,则这个几何体是 .
【答案】正五棱柱
【解析】如图所示:
由题意一个几何体由7个面围成,其中两个面是互相平行且全等的五边形,
故此几何体是五棱柱,又其他各面都是全等的矩形,
故五棱柱的上下底面边长相等且侧棱与底面垂直,
根据正棱柱的定义可知该几何体是正五棱柱.
故答案为:正五棱柱.
15.(2024·重庆万州·高一校考阶段练习)已知圆台的上底半径为2cm,下底半径为4cm,圆台的高为cm,则侧面展开图所在扇形的圆心角为 .
【答案】
【解析】把该圆台补成圆锥,圆锥的轴截面如下图所示:
过作,为垂足,
所以圆台的母线,
因为上底半径长为下底半径的一半,
所以圆锥的母线长为,
所以侧面展开图所在扇形的圆心角为,
故答案为:
16.(2024·辽宁大连·高一大连八中校考阶段练习)建筑学上,建筑师利用各种弯曲空间可以建造出很多外型美观的建筑物。刻画空间的弯曲性是几何研究的重要内容.在几何学中可用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,大小用弧度制表示),多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为,故其总曲率为.则正方体的总曲率为 ;正四棱锥的总曲率为 .
【答案】
【解析】正方体在每个顶点处有3个面角,每个面角的大小是,
所以在各顶点处的曲率为,故其总曲率为;
正四棱锥有5个顶点,5个面,其中4个三角形,1个四边形,
所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,
所以面角和为,
故总曲率为.
故答案为:;.
四、解答题
17.(2024·江苏·高一专题练习)如图所示,长方体.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
【解析】(1)是棱柱,并且是四棱柱,因为长方体相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义.因为底面是四边形,所以长方体是四棱柱;
(2)截面BCNM上方部分是棱柱,且是三棱柱,其中和是底面.
截面BCNM下方部分也是棱柱,且是四棱柱,
其中四边形和是底面.
18.(2024·高一课时练习)如图是一个圆锥形物体,其母线长为3cm,一只小虫子从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,若该小虫子爬行的最短路程为,求圆锥底面圆的半径.
【解析】作出该圆锥的侧面展开图,如图所示,易知该小虫子爬行的最短路程为,,,在中,由余弦定理得,
因为为三角形的内角,
所以,设圆锥底面圆的半径为,则,解得.
故圆锥底面圆的半径为1cm.
19.(2024·高一课时练习)将常见的几个棱柱、棱锥、棱台的顶点数(V)、面数(F)、棱数(E)作如下统计:
(1)把上表中空缺的数据补上;
(2)由此表可猜得棱柱、棱锥、棱台的顶点数(V)、面数(F)、棱数(E)满足一个关系式:_____________,并用石膏晶体和明矾晶体的空间图形中顶点数、面数、棱数验证你猜测的关系式的正确性.
【解析】(1)
(2)由于,,,,,,……,
所以,猜想棱柱、棱锥、棱台的顶点数()、面数()、棱数()满足.
验证如下:
显然,顶点数()、面数()、棱数()满足.
空间图形
顶点数
面数
棱数
三棱锥
4
三棱柱
5
三棱台
9
四棱锥
5
四棱柱
21
四棱台
8
五棱锥
10
五棱柱
10
五棱台
7
……
空间图形
顶点数
面数
棱数
三棱锥
4
4
6
三棱柱
6
5
9
三棱台
6
5
9
四棱锥
5
5
8
四棱柱
8
6
12
四棱台
8
6
12
五棱锥
6
6
10
五棱柱
10
7
15
五棱台
10
7
15
……
空间图形
顶点数
面数
棱数
石膏晶体
20
12
30
明矾晶体
12
8
18
【寒假作业】沪教版2020 高中数学 高二寒假巩固提升训练 专题09+双曲线(四大核心考点六种题型)-练习.zip: 这是一份【寒假作业】沪教版2020 高中数学 高二寒假巩固提升训练 专题09+双曲线(四大核心考点六种题型)-练习.zip,文件包含寒假作业沪教版2020高中数学高二寒假巩固提升训练专题09双曲线四大核心考点六种题型原卷版docx、寒假作业沪教版2020高中数学高二寒假巩固提升训练专题09双曲线四大核心考点六种题型解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】高中数学 高一寒假巩固提升训练 专题08+立体图形的直观图(三大考点)-练习: 这是一份【寒假作业】高中数学 高一寒假巩固提升训练 专题08+立体图形的直观图(三大考点)-练习,文件包含寒假作业高中数学高一寒假巩固提升训练专题08立体图形的直观图三大考点原卷版docx、寒假作业高中数学高一寒假巩固提升训练专题08立体图形的直观图三大考点解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】高中数学 高一寒假巩固提升训练 专题05+复数的概念(五大考点)-练习: 这是一份【寒假作业】高中数学 高一寒假巩固提升训练 专题05+复数的概念(五大考点)-练习,文件包含寒假作业高中数学高一寒假巩固提升训练专题05复数的概念五大考点原卷版docx、寒假作业高中数学高一寒假巩固提升训练专题05复数的概念五大考点解析版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。