【寒假作业】沪教版2020 高中数学 高二寒假巩固提升训练 专题01+直线的倾斜角与斜率-练习.zip

这是一份【寒假作业】沪教版2020 高中数学 高二寒假巩固提升训练 专题01+直线的倾斜角与斜率-练习.zip，文件包含寒假作业沪教版2020高中数学高二寒假巩固提升训练专题01直线的倾斜角与斜率原卷版docx、寒假作业沪教版2020高中数学高二寒假巩固提升训练专题01直线的倾斜角与斜率解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。


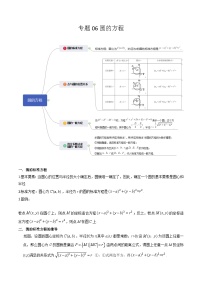
直线的倾斜角
1.定义：当直线与轴相交时，我们取轴作为基准，轴正向与直线向上方向之间所成的角叫做直线的倾斜角.
2.取值范围：直线的倾斜角的取值范围是，并规定与轴平行或重合的直线的倾斜角为.
补充：（1）倾斜角与直线倾斜程度的关系
(2)对直线的倾斜角的理解
①倾斜角直观地表示了直线相对于轴正方向的倾斜程度.
②平面内任何一条直线都有唯一的倾斜角，不同的直线可以有相同的倾斜角.
直线的斜率
1.定义：一条直线的倾斜角的正切值叫做这条直线的斜率，斜率常用小写字母表示，即.
注意：当直线的倾斜角为90°时，直线的斜率不存在，并不是该直线不存在，而是该直线垂直于轴（平行于轴或与轴重合）.因此，所有直线都有倾斜角，但不是所有直线都有斜率.
2.倾斜角与斜率的关系
补充：斜率和倾斜角的特点
①斜率和倾斜角都反映直线的倾斜程度，其中斜率是从代数角度描述的，倾斜角是从几何角度描述的；
②直线的斜率是随着倾斜角的变化而变化的，并且当直线的倾斜角不是90°时，倾斜角相同的直线，其斜率相同，倾斜角不同的直线，其斜率不同；
③直线有斜率必有倾斜角，倾斜角是90°的直线没有斜率，倾斜角不是90°的直线都有斜率.
直线斜率的坐标表示
1．公式：经过两点的直线的斜率公式为．
2．公式的推导
如图，设直线的倾斜角为α（α≠90°），当直线的方向（即从指向的方向）向上时，过点作x轴的平行线，过点作y轴的平行线，两条直线相交于点Q，于是点Q的坐标为．
如图（1），当α为锐角时，．
在中，．
如图（2），当α为钝角时，α=180°−θ（设），．．
在中，，
于是可得，即．
同样，当直线的方向向上时，如图，也有，即．
综上所述，经过两点的直线的斜率公式为．
直线斜率与直线方向向量
1.若直线的斜率为，它的一个方向向量的坐标为 ，则 .
2.若直线的斜率为 且直线过两点 ，它的一个方向向量的坐标为，则.
直线的倾斜角（共5小题）
1.已知直线l的倾斜角为α-15°，则下列结论中正确的是（ ）
A．0°≤α<180°B．15°<α<180°
C．15°≤α<180°D．15°≤α<195°
【答案】D
【分析】由直线的倾斜角的取值范围求解即可.
【详解】设直线l的倾斜角为β，则β的范围是0°≤β<180°.由题意知β=α-15°，则0°≤α-15°<180°，解得15°≤α<195°.
2.（2023春·上海市奉贤中学高二第二学期期中）直线x=1的倾斜角为___________
【答案】
【分析】根据直线的方程可得出直线的倾斜角.
【详解】直线垂直于轴，故直线的倾斜角为.故答案为：.
3.（2022·上海市新中高级中学高三期中）直线 的倾斜角为_______.
【答案】
【分析】由斜率直接求出倾斜角.
【详解】由直线可得：斜率为.
设倾斜角为，所以，解得：.故答案为：
4.（2023春·上海市复旦附中高二第二学期期中）直线2x-y-1=0的倾斜角是__________.
【答案】
【分析】直接根据斜率可得倾斜角.
【详解】即，
设倾斜角为，则所以.故答案为：.
5．（2022春•嘉定区校级月考）已知直线的斜率，x≠0，则直线的倾斜角α的取值范围为 ．
【答案】
【分析】根据已知条件，结合基本不等式的公式，以及斜率与倾斜角的关系，即可求解．
【详解】当x＞0时，，当且仅当，即x＝1时，等号成立，即k＝tan α≥1，解得，
当x＜0时，，当且仅当，即x＝﹣1时，等号成立，即k＝tan α≤﹣1，解得α∈，
综上所述，直线的倾斜角α的取值范围为．
故答案为：．
二．直线的斜率（共3小题）
1.（2022•徐汇区校级开学）若直线l的倾斜角为120°则l的斜率是__________．
【答案】﹣
【分析】直接利用直线的斜率与倾斜角的关系求解即可．
【详解】解：直线l的倾斜角为120°则l的斜率是：tan120°＝．故答案为：﹣．
2．（2022春•杨浦区校级期中）设a∈R，若直线l经过点A（a，2）、B（a+1，3），则直线l的斜率是 ．
【答案】1
【分析】直接利用点的坐标求出直线的斜率．
【详解】解：直线l经过点A（a，2）、B（a+1，3），则直线的斜率．
故答案为：1．
3．（2022春•金山区期中）经过A（1，0），B（0，）两点的直线斜率为 ．
【答案】﹣
【分析】把两个点的坐标代入公式k＝，计算即可求得结论．
【详解】解：∵直线经过点A（1，0），B（0，），
∴直线的斜率为k＝＝﹣，
故答案为：﹣．
三．直线的图象特征与倾斜角、斜率的关系（共5小题）
1.（2022春•金山区期中）经过A（1，0），B（0，）两点的直线斜率为 ．
【答案】﹣
【分析】把两个点的坐标代入公式k＝，计算即可求得结论．
【详解】解：∵直线经过点A（1，0），B（0，），
∴直线的斜率为k＝＝﹣，
故答案为：﹣．
2．（2022春•嘉定区校级月考）经过两点A（1，t）、B（t+1，4）的直线的倾斜角为45°，则实数t＝ ．
【答案】2
【分析】根据已知条件，结合直线的斜率公式，以及斜率与倾斜角的关系，即可求解．
【详解】解：∵经过两点A（1，t）、B（t+1，4）的直线的倾斜角为45°，
∴tan45°＝，即﹣t＝t﹣4，解得t＝2．故答案为：2．
3．（2022春•杨浦区校级期中）设a∈R，若直线l经过点A（a，2）、B（a+1，3），则直线l的斜率是 ．
【答案】1
【分析】直接利用点的坐标求出直线的斜率．
【详解】解：直线l经过点A（a，2）、B（a+1，3），则直线的斜率．
4．（2022春•黄浦区校级月考）直线l经过点（﹣2，0）和（1，），则直线l的倾斜角为 ．
【答案】
【分析】由题意，利用直线的斜率公式，直线的倾斜角和斜率的定义，得出结论．
【详解】解：∵直线l经过点（﹣2，0）和（1，），
∴直线l的斜率为＝，故直线的倾斜角为，
故答案为：．
5．若图中的直线l1，l2，l3的斜率分别为k1，k2，k3，则（ ）
A．k1＜k2＜k3B．k3＜k1＜k2C．k3＜k2＜k1D．k1＜k3＜k2
【答案】D
【分析】由直线斜率（倾斜角的正切值）的定义和正切函数的单调性可得．
【详解】解：直线l1的倾斜角是钝角，则斜率k1＜0；
直线l2与l3的倾斜角都是锐角，斜率都是正数，
但直线l2的倾斜角大于l3的倾斜角，所以k2＞k3＞0，
所以k1＜k3＜k2，故选：D．
四．直线斜率与直线方向向量（共4小题）
1.过A(4,y),B(2,-3)两点的直线的一个方向向量为n=(-1,-1),则y= ( )
A. B. QUOTE C.-1D.1
【答案】C
【分析】由A，B坐标，可以求得，然后与方向向量平行，可以求得y值
【详解】解法一:由直线上的两点A(4,y),B(2,-3),得 QUOTE =(-2,-3-y),
又直线AB的一个方向向量为n=(-1,-1),因此n∥ QUOTE ,
∴(-2)×(-1)-(-3-y)×(-1)=0,解得y=-1,故选C.
解法二:由直线的方向向量为(-1,-1)得,直线的斜率为 QUOTE =1,所以 QUOTE =1,解得y=-1.故选C.
2.直线x﹣2y+1＝0的一个方向向量是（ ）
A．（1，﹣2）B．（1，2）C．（2，﹣1）D．（2，1）
【答案】D
【分析】首先求出直线的斜率，进一步利用直线的斜率和方向向量对应相等求出结果
【详解】直线x﹣2y+1＝0的斜率k＝．即与向量＝（2，1）共线，故选：D．
3.（2023秋·上海市松江区·阶段练习）若直线l的一个方向向量，则直线l的倾斜角是 .
【答案】
【分析】根据直线的一个方向向量，设直线的倾斜角为，则，由此得到直线的倾斜角.
【详解】直线的一个方向向量，
设直线的倾斜角为，则，
又因为，且，所以，所以.
故答案为：.
4．（2022·上海市控江中学高一期末）若直线的一个方向向量，则与直线的夹角的余弦值______.
【答案】.
【分析】根据题意可得两直线的倾斜角分别为，，进而可得两直线的夹角为，再由两角和的余弦公式即可求得答案.
【详解】解：因为直线的一个方向向量，
所以直线的斜率，所以直线的倾斜角为，
又因为直线的斜率，所以线的倾斜角为，
所以直线与直线的夹角，
所以.
故答案为：.
一、填空题
1.（2022·上海市宝山中学高二期中）已知直线：，则此直线的倾斜角为_________.
【答案】
【分析】先求得直线的斜率，然后求得直线的倾斜角.
【详解】直线的斜率为，所以倾斜角为.
故答案为：
2.（2020·上海·位育中学高二期中）若是直线的一个方向向量，则的倾斜角的大小为________.
【答案】
【分析】由方向向量，斜率与倾斜角的关系求解
【详解】由得，故倾斜角的大小为，
故答案为：
3.（2022·上海崇明·高二期末）直线的倾斜角的大小等于_____________．
【答案】
【分析】根据直线的斜率与倾斜角的关系求解即可.
【详解】解：设直线的倾斜角为
由题知，直线的斜率，所以故答案为：
4.（2022·上海·高二专题练习）直线经过点和，则直线的倾斜角为______
【答案】
【分析】先利用直线的斜率公式求出斜率，再求其倾斜角.
【详解】由题意，得直线的斜率为，又
所以直线的倾斜角为.
故答案为：.
5.（2022·上海·高二专题练习）经过两点的直线的倾斜角为，则___________.
【答案】2
【分析】由两点间的斜率公式及直线斜率的定义即可求解.
【详解】解：因为过两点的直线的倾斜角为，
所以，解得，
故答案为：2.
6.（2023年春·上海南洋模范中学高二下期中）直线的倾斜角的取值范围是_______.
【答案】
【分析】根据直线斜率，可知，结合可求得结果.
【详解】由知：直线斜率，
设直线倾斜角为，则，又，.
故答案为：.
7.（2022春·上海市奉贤中学校考期中）已知θ∈0,π2，试用θ表示经过P(0,0),Q(sinθ,csθ)两点直线l的倾斜角_____．
【答案】π2−θ
【分析】由斜率公式求解得到答案，注意角度的范围
【详解】设直线l的倾斜角为α，
∵θ∈0,π2，则sinθ≠0，
∴tanα=csθsinθ=sin(π2−θ)cs(π2−θ)=tan(π2−θ)，
又∵θ∈0,π2,α∈0,π，则π2−θ∈0,π2，
∴α=π2−θ.
故答案为：π2−θ.
8.（2022秋·上海市七宝中学高二上期末）已知直线经过点，且它的倾斜角等于直线的倾斜角的倍，则直线的方程为 _________ ．
【答案】
【分析】求出直线的倾斜角，从而可求得直线的倾斜角，即可得解.
【详解】解：直线的倾斜角为，所以直线的倾斜角为，
所以直线的方程为．
故答案为：x = -2
9.（2022秋·上海静安·高二校考期末）直线的倾斜角为______.
【答案】
【分析】首先根据已知条件得到直线的斜率，再求倾斜角即可.
【详解】直线的斜率，则倾斜角为.
故答案为：
10.（2021秋•徐汇区校级期末）直线的倾斜角是 ．
【答案】60°
【分析】设此直线的倾斜角为θ，则tan θ＝，且 0≤θ＜π，从而得到 θ＝60°．
【详解】解：直线的斜率为，设此直线的倾斜角为θ，则tan θ＝，且 0≤θ＜π，
∴θ＝60°，
故答案为：60°．
11.（2021秋•青浦区校级月考）已知点A（﹣3，4），B（3，2），过点P（1，0）的直线l与线段AB有公共点，则直线l的倾斜角的取值范围 ．
【答案】45°≤α≤135°
【分析】由题意画出图形，求出P与线段AB端点连线的倾斜角得答案．
【详解】如图，当直线l过B时设直线l的倾斜角为α（0≤α＜π），
则tan α＝＝1，α＝45°
当直线l过A时设直线l的倾斜角为β（0≤β＜π），
则tan β＝＝﹣1，β＝135°，
∴要使直线l与线段AB有公共点，
则直线l的倾斜角α的取值范围是45°≤α≤135°．
故答案为45°≤α≤135°．
12．（2022·上海市青浦高级中学高二阶段练习）已知线段两端点的坐标分别为和，若直线恒过，且与线段有交点，则的斜率的取值范围是_____．
【答案】
【分析】根据已知条件及直线的斜率公式即可求解.
【详解】因为直线恒过,和，
所以，.
由题意可知，直线的斜率存在且的斜率，若直线与线段有交点，如图所示
由图象可知，或,即或，
所以的斜率的取值范围是为.
故答案为：.
二、单选题
13．（2022·上海市朱家角中学高一期末）已知直线与直线，若直线与直线的夹角为，则实数的值为（ ）
A．B．C．或0D．或
【答案】C
【分析】根据倾斜角与斜率的关系即可求解.
【详解】的斜率为，所以其倾斜角为，直线恒过点,若直线与直线的夹角为，则的倾斜角为或者，所以斜率为或，
故选：C
14.已知点A（2，4），B（3，6），则直线AB的斜率为（ ）
A．B．C．2D．-2
【答案】C
【分析】直角利用两点坐标求直线斜率的公式计算即可.
【详解】因为，所以.故选：C
15.（2023年春·上海格致中学高二下期中）若直线的一个方向向量为，则它的倾斜角为（ ）
A. B. C. D.
【答案】C
【分析】由题意，求出直线的斜率，从而得出结果．
【详解】依题意，是直线的一个方向向量，
所以直线的斜率，
所以直线的倾斜角为．故选：C．
16.（2021秋•浦东新区校级月考）已知下列命题：
①直线的倾斜角为α，则此直线的斜率为tanα；
②直线的斜率为tanα，则直线的倾斜角为α；
③直线的倾斜角为α，则sinα＞0．
上述命题中不正确的是（ ）
A．①②B．①③C．②③D．①②③
【答案】D
【分析】根据直线的倾斜角与斜率的定义，判断即可．
【详解】对于①，直线的倾斜角为α，α＝90°，直线的斜率不存在，α≠90°时，直线的斜率为tan α，所以①错误；
对于②，直线的斜率为tan α时，α不一定是直线的倾斜角，如α＝﹣45°时，直线的斜率为﹣1，倾斜角为135°，所以②错误；
对于③，直线的倾斜角为α，α＝0时，sinα＝0，所以③错误．
综上知，错误的命题序号是①②③．
故选：D．
三、解答题
17. 已知两点A(－3,4)，B(3,2)，过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围；
(2)求直线l的倾斜角α的取值范围．
【答案】（1）或；（2）
【分析】（1）由题意画出图形，求出与线段端点连线的倾斜角得答案；（2）由斜率是倾斜角的正切值即可得到的斜率的取值范围.
【详解】如图，由题意可知，直线的斜率，直线的斜率，
(1)要使与线段有公共点，则直线的斜率的取值范围是，或.
(2)由题意可知直线l的倾斜角介于直线与的倾斜角之间，又直线的倾斜角是，直线的倾斜角是，故的取值范围是.
18．已知直线.
（1）若直线过点，试写出直线的一个方向向量；
（2）若实数，求直线的倾斜角的取值范围.
【答案】（1）直线的一个方向向量为；（2）.
【分析】（1）将A代入直线l方程求a，写出直线方程即可得l的方向向量；
（2）由直线方程得斜率，讨论a并利用基本不等式求k的范围，进而可得倾斜角的范围.
【详解】（1）把代入直线的方程，得，解得，此时直线的方程为，
故直线的一个方向向量为；
（2）因为，所以直线的斜率，
∴当时，当且仅当时等号成立；
当时，当且仅当时等号成立；
综上有，可得倾斜角.
19．已知坐标平面内两点M(m＋3,2m＋5)，N(m－2,1).
(1)当m为何值时，直线MN的倾斜角为锐角？
(2)当m为何值时，直线MN的倾斜角为钝角？
(3)直线MN的倾斜角可能为直角吗？
【答案】(1) m>－2. (2) m<－2. (3) 不可能为直角.
【分析】(1)由倾斜角为锐角，则斜率大于0，根据斜率公式，得到不等式，即可求解；
(2)由倾斜角为钝角，则斜率小于0，根据斜率公式，得到不等式，即可求解；
(3)当直线MN垂直于x轴时直线的倾斜角为直角，此时m＋3＝m－2，即可作出判定．
【详解】(1)若倾斜角为锐角，则斜率大于0，
即k＝＝>0，
解得m>－2.
(2)若倾斜角为钝角，则斜率小于0，
即k＝＝<0，
解得m<－2.
(3)当直线MN垂直于x轴时直线的倾斜角为直角，此时m＋3＝m－2，此方程无解，故直线MN的倾斜角不可能为直角.
20．已知过原点O的一条直线与函数的图像交于A，B两点，分别过点A，B作y轴的平行线与函数的图像交于C，D两点．
（1）证明：点O，C，D在同一条直线上；
（2）当直线平行于x轴时，求点A的坐标．
【答案】（1）证明见解析；（2）．
【分析】（1）设出、的坐标，解出、的坐标，求出、的斜率相等则三点共线．
（2）平行轴，、纵坐标相等，推出横坐标的关系，结合（1）即可求出的坐标．
【详解】（1）设点、的横坐标分别为、由题设知，，．则点、纵坐标分别为、．
因为、在过点的直线上，所以，
点、坐标分别为，，，．
由于，
的斜率，
的斜率．
由此可知，，
即、、在同一条直线上．
（2）由于平行于轴知
，
即得，
．
代入得．
由于知，
．
考虑解得．
于是点的坐标为，．
21.已知直线：的倾斜角为角.
（1）求；
（2）求，的值.
【答案】（1）；（2）；
【分析】（1）首先求出直线的斜率，再根据斜率等于倾斜角的正切值计算可得；
（2）利用同角三角函数的基本关系及二倍角公式计算可得；
【详解】（1）因为直线的斜率为，且直线的倾斜角为角，
所以
（2）由（1）知，
解得或，
因为，所以
目录
新知导航：熟悉课程内容、掌握知识脉络
基础知识：知识点全面梳理，掌握必备
学以致用：考点剖析，提升能力
小试牛刀：过关检测，成果评定
倾斜角
直线
直线情况
平行于轴
由左向右上升
垂直于轴
由左向右下降
的大小
0°
的范围
0
不存在
的增减性
随增大而增大
随增大而增大