【寒假作业】（沪教版2020）高中数学 高一寒假巩固提升训练 专题05诱导公式（6种题型）-练习

这是一份【寒假作业】（沪教版2020）高中数学 高一寒假巩固提升训练 专题05诱导公式（6种题型）-练习，文件包含寒假作业沪教版2020高中数学高一寒假巩固提升训练专题05诱导公式6种题型原卷版docx、寒假作业沪教版2020高中数学高一寒假巩固提升训练专题05诱导公式6种题型解析版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。

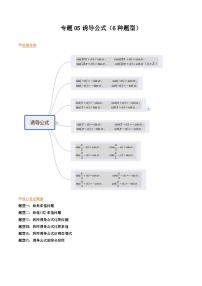
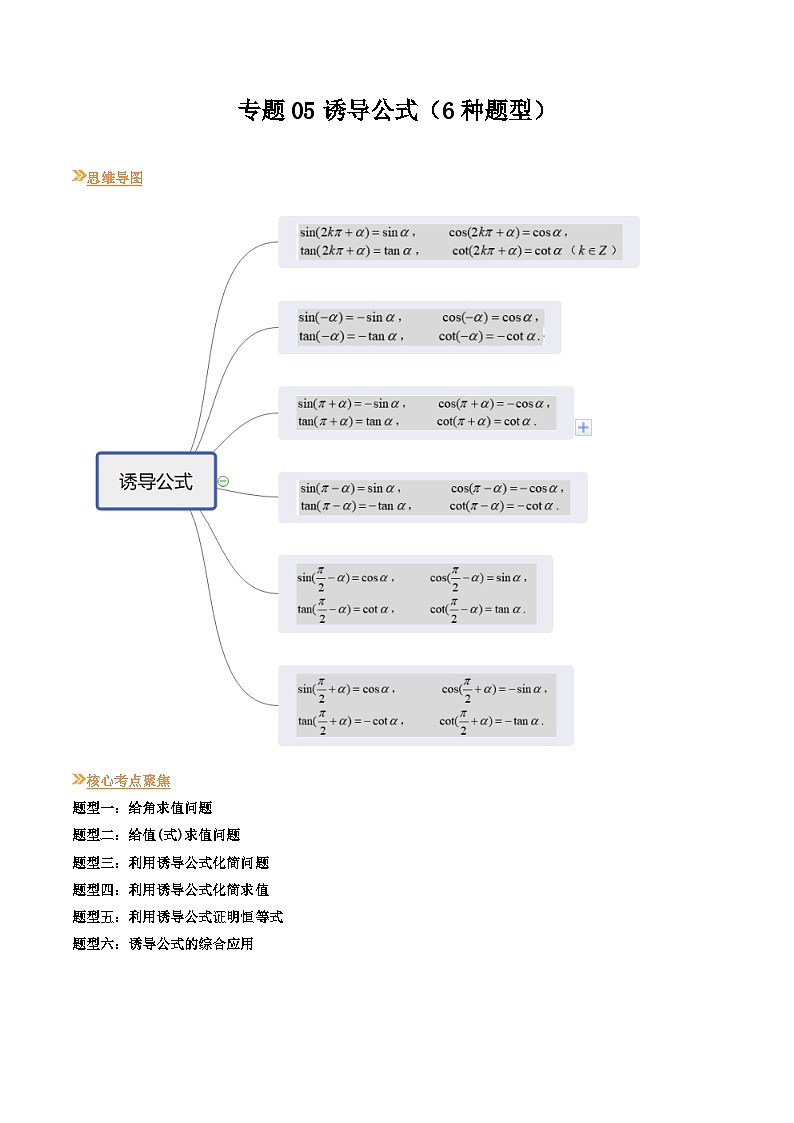
思维导图
核心考点聚焦
题型一：给角求值问题
题型二：给值(式)求值问题
题型三：利用诱导公式化简问题
题型四：利用诱导公式化简求值
题型五：利用诱导公式证明恒等式
题型六：诱导公式的综合应用
（），，，这些角都与角有特殊的关系. 已知角的正弦、余弦、正切及余切值，能够快速求出上述这些角的正弦、余弦、正切及余切值？这就是诱导公式要解决的问题.
由于角（）的终边与角的终边重合，因此由定义有如下诱导公式：
， ，
， （）.
由这组诱导公式，求任意角的正弦、余弦、正切及余切值可以转化为求范围内一个角的相应值.
角的终边与角的终边关于周对称，角的终边与单位圆交于点，而角的终边与单位圆交于点. 由于点与点关于轴对称，其横坐标相等，而纵坐标互为相反数，因此有如下诱导公式：
， ，
， .
由这组诱导公式，求负角的正弦、余弦、正切及余切值可以转化为求正角的相应值.
将角的终边绕着原点按逆时针方向旋转弧度，得到角的终边，这说明角和角的终边在同一条直线上，但方向相反. 角的终边与单位圆交于点. 由于点与点关于原点对称，其横坐标和纵坐标都互为相反数，因此有如下诱导公式：
， ，
， .
由这组诱导公式，求范围内的角的正弦、余弦、正切及余切值可以转化到范围内一个角的相应值.
角的终边与角的终边关于轴对称，角的终边与单位圆交于点，而角的终边与单位圆交于点. 由于点与点关于轴对称，其横坐标互为相反数，而纵坐标互相等，因此有如下诱导公式：
， ，
， .
由这组诱导公式，求范围内的角的正弦、余弦、正切及余切值可以转化到范围内一个角的相应值.
以上四组诱导公式说明，（），，的正弦、余弦、正切及余切值的绝对值等于角的相应量的绝对值【名称不变】，但这两个值之间可能差一个正负号. 由于诱导公式较多，记忆其中的正负号并不容易，但有一个简单的方法可以加以判断，即：当为锐角时，等式两边必须同正或同负.
例如，的绝对值应该与的绝对值相等，即成立. 但当为锐角时，是第二象限的角【符号看象限】，这时，而，所以前式中应该取负号，即有.
角的终边与角关于直线对称，角的终边与单位圆交于点，而角的终边与单位圆交于点. 由于点与点关于直线对称，则点的横坐标与点的纵坐标相等，而点的纵坐标与点的横坐标相等，因此有如下诱导公式：
， ，
， .
在以上公式中将用代换，就有.
同理，有如下诱导公式：
， ，
， .
上述两组诱导公式说明正弦和余弦可以相互转化，正切和余切也可以相互转化.
以上两组诱导公式说明角的正（余）弦、正（余）切值的绝对值，必等于角的余（正）弦、余（正）切值的绝对值【名称改变】，但这两者可能差一个正负号. 这个正负号的确定方法是：当角为锐角时，等式两边必须同正或同负. 例如，的绝对值应该同的绝对值相等，即成立. 但当为锐角时，是第二象限的角【符号看象限】，这时，而，所以前式中应该取负号，即有.
奇变偶不变，符号看象限.
例如，及都是的奇数倍，如果等式左边是，的正弦、余弦、正切、余切之一，那么等式右边相应的必定是的余弦、正弦、余切、正切，这就是“奇变”；而（）、、都是的偶数倍，等式两边的正弦、余弦、正切及余切的名称就应该相同，这就是“偶不变”. 等式右边角正弦、余弦、正切及余切前的符号可以将视为锐角（实际上此时可以为任意角），由等式左边的角所在的象限的正弦、余弦、正切及余切值的符号来确定，即“符号看象限”.
题型一：给角求值问题
【例1】 求下列各三角函数值：
(1)sin 1 320°；(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(31π,6)))；(3)tan(－945°)．
【变式】计算：(1)cseq \f(π,5)＋cseq \f(2π,5)＋cseq \f(3π,5)＋cseq \f(4π,5)；
(2)tan 10°＋tan 170°＋sin 1 866°－sin(－606°)．
题型二：给值(式)求值问题
【例2】 (1)已知sin(α－360°)－cs(180°－α)＝m，则sin(180°＋α)·cs(180°－α)等于( )
A.eq \f(m2－1,2) B.eq \f(m2＋1,2)
C.eq \f(1－m2,2) D．－eq \f(m2＋1,2)
(2)已知cs(α－75°)＝－eq \f(1,3)，且α为第四象限角，求sin(105°＋α)的值．
题型三：利用诱导公式化简问题
【例3】 设k为整数，化简：
eq \f(sinkπ－αcs[k－1π－α],sin[k＋1π＋α]cskπ＋α).
【变式】．化简：(1)eq \f(tan2π－αsin－2π－αcs6π－α,csα－πsin5π－α)；
(2)eq \f(sin1 440°＋α·cs1 080°－α,cs－180°－α·sin－α－180°).
题型四：利用诱导公式化简求值
【例4】 (1)已知cs 31°＝m，则sin 239°tan 149°的值是( )
A.eq \f(1－m2,m) B.eq \r(1－m2)
C．－eq \f(1－m2,m) D．－eq \r(1－m2)
(2)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－α))＝eq \f(1,2)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)＋α))的值为________．
题型五：利用诱导公式证明恒等式
【例5】 (1)求证：
eq \f(sin θ＋cs θ,sin θ－cs θ)＝eq \f(2sin\b\lc\(\rc\)(\a\vs4\al\c1(θ－\f(3π,2)))cs\b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,2)))－1,1－2sin2π＋θ).
(2)求证：eq \f(cs6π＋θsin－2π－θtan2π－θ,cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋θ))sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋θ)))＝－tan θ.
【变式】．求证：eq \f(cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋x)),sin\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(5π,2)))tan6π－x)＝－1.
题型六：诱导公式的综合应用
【例6】 已知sin α是方程5x2－7x－6＝0的根，α是第三象限角，求eq \f(sin\b\lc\(\rc\)(\a\vs4\al\c1(－α－\f(3,2)π))cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)π－α)),cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α)))·tan2(π－α)的值．
【变式】．已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)－α))·cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(5π,2)－α))＝eq \f(60,169)，且eq \f(π,4)＜α＜eq \f(π,2)，求sin α与cs α的值．
一、填空题
1、化简：________
2、化简=
3、计算__________________
4、已知，则的值为
5、已知，且是第二象限角，则的值等于_______
6、计算：sin 585°cs 1 290°＋cs(－30°)sin 210°＋tan 135°=
7、若，则__________
8、若，则
9、化简：___________.
10、已知角α终边上一点P(－4，3)，则eq \f(cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))sin－π－α,cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(11π,2)－α))sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(9π,2)＋α)))的值为____________．
11、若＝，则的值是________．
12．已知cs α＝eq \f(1,5)，且α为第四象限角，那么cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,2)))＝________.
二、选择题
13、已知，则（ ）
A．0B．mC．mD．不确定
14、已知，化简： （ ）
A． B． C．D．随k的变化而变化
15、已知，则的值是( )
A. B. C. D.
16、化简，得（ ）
A．1 B．C． D．
三、解答题
17、已知，
（1）求的值；
（2）求：的值；
18.如图，已知点的坐标为，将绕坐标原点逆时针旋转至. 求点的坐标.
19、已知sin α是方程5x2－7x－6＝0的根，且α为第三象限角，
求：eq \f(sin\b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(3π,2)))·sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)－α))·tan22π－α·tanπ－α,cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))·cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α)))的值
20、已知α是第三象限角，且f(α)＝eq \f(sinπ－αcs2π－αsin\b\lc\(\rc\)(\a\vs4\al\c1(－α＋\f(3π,2))),sin－π－αsin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))).
（1）求f(α)；（2）若cseq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(3π,2)))＝eq \f(1,5)，求：f(α)．
21、（1）求函数的值域；
（2）化简：．