2023-2024学年北京市101中学九上数学期末调研模拟试题含答案

这是一份2023-2024学年北京市101中学九上数学期末调研模拟试题含答案，共8页。试卷主要包含了抛物线的顶点在等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题(每小题3分,共30分)
1．下列手机应用图标中，是中心对称图形的是（ ）
A．B．C．D．
2．某同学用一根长为（12+4π）cm的铁丝，首尾相接围成如图的扇形（不考虑接缝），已知扇形半径OA＝6cm，则扇形的面积是（ ）
A．12πcm2B．18πcm2C．24πcm2D．36πcm2
3．对于抛物线，下列说法正确的是（ ）
A．开口向下，顶点坐标B．开口向上，顶点坐标
C．开口向下，顶点坐标D．开口向上，顶点坐标
4．如图，点A、B、C在⊙O上，∠ACB＝130°，则∠AOB的度数为（ ）
A．50°B．80°C．100°D．110°
5．已知的三边长分别为、、，且满足，则的形状是（ ）．
A．等边三角形B．等腰三角形C．等腰直角三角形D．直角三角形
6．下列图形中，绕某个点旋转72度后能与自身重合的是（ ）
A．B．
C．D．
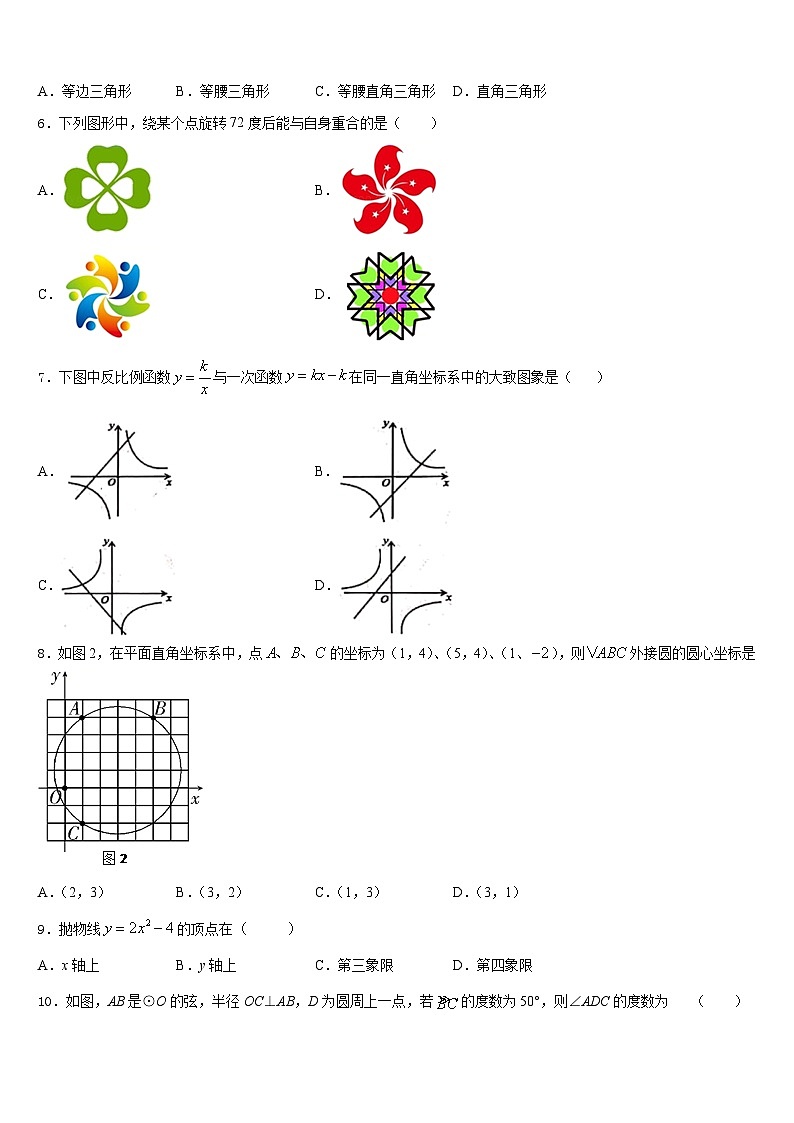
7．下图中反比例函数与一次函数在同一直角坐标系中的大致图象是（ ）
A．B．
C．D．
8．如图2，在平面直角坐标系中，点的坐标为（1，4）、（5，4）、（1、），则外接圆的圆心坐标是
A．（2，3）B．（3，2）C．（1，3）D．（3，1）
9．抛物线的顶点在（ ）
A．x轴上B．y轴上C．第三象限D．第四象限
10．如图，AB是⊙O的弦，半径OC⊥AB，D为圆周上一点，若的度数为50°，则∠ADC的度数为 （ ）
A．20°B．25°C．30°D．50°
二、填空题(每小题3分,共24分)
11．扫地机器人能够自主移动并作出反应，是因为它发射红外信号反射回接收器，机器人在打扫房间时，若碰到障碍物则发起警报．若某一房间内A、B两点之间有障碍物，现将A、B两点放置于平面直角坐标系xOy中（如图），已知点A，B的坐标分别为(0，4)，(6，4)，机器人沿抛物线y＝ax2﹣4ax﹣5a运动．若机器人在运动过程中只触发一次报警，则a的取值范围是_____．
12．某剧场共有个座位，已知每行的座位数都相同，且每行的座位数比总行数少，求每行的座位数．如果设每行有个座位，根据题意可列方程为_____________．
13．一元二次方程配方后得，则的值是__________．
14．如图，是的两条切线，为切点，点分别在线段上，且，则__________．
15．抛物线y=﹣x2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是_____．
16．已知正方形ABCD边长为4，点P为其所在平面内一点，PD＝，∠BPD＝90°，则点A到BP的距离等于_____．
17．已知△ABC中，∠BAC=90°，用尺规过点A作一条直线，使其将△ABC分成两个相似的三角形，其作法不正确的是_______．（填序号）
18．布袋里有8个大小相同的乒乓球，其中2个为红色，1个为白色，5个为黄色，搅匀后从中随机摸出一个球是红色的概率是__________.
三、解答题(共66分)
19．（10分）如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，求抛物线经过A（1，0），C（0，3）两点，与x轴交于A、B两点．
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在该抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为该抛物线的对称轴x=﹣1上的一个动点，直接写出使△BPC为直角三角形的点P的坐标．
（提示：若平面直角坐标系内有两点P（x1，y1）、Q（x2，y2），则线段PQ的长度PQ=）．
20．（6分）一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，
（1）求点C到直线AB的距离；
（2）求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cs53°≈0.6）
21．（6分）如图，已知抛物线经过的三个顶点，其中点，点，轴，点是直线下方抛物线上的动点.
（1）求抛物线的解析式；
（2）过点且与轴平行的直线与直线、分别交与点、，当四边形的面积最大时，求点的坐标；
（3）当点为抛物线的顶点时，在直线上是否存在点，使得以、、为顶点的三角形与相似，若存在，直接写出点的坐标；若不存在，请说明理由.
22．（8分）如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于点和．
求一次函数和反比例函数的表达式；
请直接写出时，x的取值范围；
过点B作轴，于点D，点C是直线BE上一点，若，求点C的坐标．
23．（8分）若，且3a+2b﹣4c=9，求a+b﹣c的值是多少？
24．（8分）解不等式组并求出最大整数解.
25．（10分）先化简，再求值：（）÷，其中a是一元二次方程对a2+3a﹣2＝0的根．
26．（10分）如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．
（1）求证：OP⊥CD；
（2）连接AD，BC，若∠DAB＝50°，∠CBA＝70°，OA＝2，求OP的长．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、A
4、C
5、D
6、B
7、B
8、D
9、B
10、B
二、填空题(每小题3分,共24分)
11、﹣＜a＜
12、x(x+12)=1
13、1
14、61°
15、－3＜x＜1
16、或
17、③
18、
三、解答题(共66分)
19、（1）y=x+3；y=﹣x2﹣2x+3；（2）M的坐标是（﹣1，2）；（3）P的坐标是（﹣1，）或（﹣1，）或（﹣1，4）或（﹣1，﹣2）．
20、（1）40海里；（2）小时．
21、（1）；（2）；（3）存在， ，
22、反比例函数的解析式为，一次函数解析式为：；当或时，；当点C的坐标为或时，．
23、﹣1．
24、最大整数解为
25、a1+3a，1
26、（1）详见解析；（2）.