2023-2024学年四川省成都市七中学育才学校数学九上期末教学质量检测试题含答案

这是一份2023-2024学年四川省成都市七中学育才学校数学九上期末教学质量检测试题含答案，共9页。试卷主要包含了若两个相似三角形的周长之比是1，抛物线的顶点坐标是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图，在一幅长，宽的矩形风景画的四周镶一条金色纸边，制成一幅矩形图，如果要使整个挂图的面积是，设金色纸边的宽为，那么满足的方程是（ ）
A．B．
C．D．
2．若点，在反比例函数上，则的大小关系是（ ）
A．B．C．D．
3．如图，某水库堤坝横断面迎水坡AB的坡比是1：，堤坝高BC=50m，则应水坡面AB的长度是（ ）
A．100mB．100mC．150mD．50m
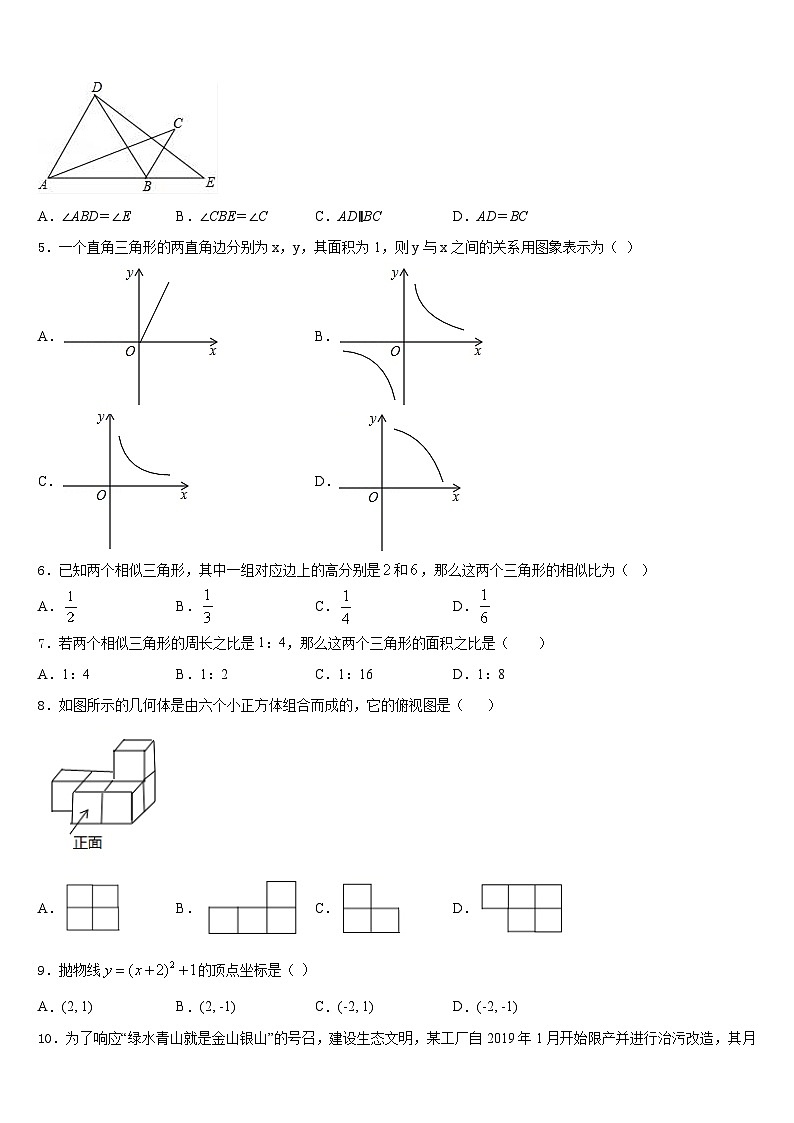
4．如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（ ）
A．∠ABD＝∠EB．∠CBE＝∠CC．AD∥BCD．AD＝BC
5．一个直角三角形的两直角边分别为x，y，其面积为1，则y与x之间的关系用图象表示为（ ）
A．B．
C．D．
6．已知两个相似三角形，其中一组对应边上的高分别是和，那么这两个三角形的相似比为（ ）
A．B．C．D．
7．若两个相似三角形的周长之比是1：4，那么这两个三角形的面积之比是（ ）
A．1：4B．1：2C．1：16D．1：8
8．如图所示的几何体是由六个小正方体组合而成的，它的俯视图是（ ）
A．B．C．D．
9．抛物线的顶点坐标是（ ）
A．(2, 1)B．(2, -1)C．(-2, 1)D．(-2, -1)
10．为了响应“绿水青山就是金山银山”的号召，建设生态文明，某工厂自2019年1月开始限产并进行治污改造，其月利润(万元)与月份之间的变化如图所示，治污完成前是反比例函数图象的一部分，治污完成后是一次函数图象的部分，下列选项错误的是（ ）
A．4月份的利润为万元
B．污改造完成后每月利润比前一个月增加万元
C．治污改造完成前后共有个月的利润低于万元
D．9月份该厂利润达到万元
二、填空题(每小题3分,共24分)
11．某种药原来每瓶售价为40元，经过两次降价，现在每瓶售价为25.6元，若设平均每次降低的百分率为，根据题意列出方程为______________________．
12．二次函数解析式为，当x>1时，y随x增大而增大，求m的取值范围__________
13．抛物线经过点,则这条抛物线的对称轴是直线__________．
14．当_____时，在实数范围内有意义．
15．如图，在平面直角坐标系中，反比例函数（x＞0）与正比例函数y=kx、 （k＞1）的图象分别交于点A、B，若∠AOB＝45°，则△AOB的面积是________.
16．用反证法证明命题“若⊙O的半径为r，点P到圆心的距离为d，且d＞r，则点P在⊙O的外部”，首先应假设P在__________．
17．一个不透明的口袋中装有若干只除了颜色外其它都完全相同的小球，若袋中有红球6只，且摸出红球的概率为，则袋中共有小球_____只．
18．如图，转盘中个扇形的面积都相等．任意转动转盘次，当转盘停止转动时，指针落在阴影部分的概率为________．
三、解答题(共66分)
19．（10分）计算：（1）；
（2）先化简，再求值．，其中a=2020；
20．（6分）初三（1）班要从2男2女共4名同学中选人做晨会的升旗手．
（1）若从这4人中随机选1人，则所选的同学性别为男生的概率是 ．
（2）若从这4人中随机选2人，求这2名同学性别相同的概率．
21．（6分）如图，在平面直角坐标系中，点从点运动到点停止，连接，以长为直径作.
（1）若，求的半径；
（2）当与相切时，求的面积；
（3）连接，在整个运动过程中，的面积是否为定值，如果是，请直接写出面积的定值，如果不是，请说明理由.
22．（8分）定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形中，若，则称四边形为准平行四边形.
（1）如图①，是上的四个点，，延长到，使.求证:四边形是准平行四边形；
（2）如图②，准平行四边形内接于，，若的半径为，求的长；
（3）如图③，在中，，若四边形是准平行四边形，且，请直接写出长的最大值.
23．（8分）为了解学生的艺术特长发展情况，某校决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中，你最喜欢哪一项活动（每人只限一项）”的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如下两幅不完整的统计图．
请你根据统计图解答下列问题：
（1）扇形统计图中“戏曲”部分对应的扇形的圆心角为 度；
（2）若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组，请用列举法求恰好选中“舞蹈、声乐”这两项的概率．
24．（8分）若x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：，.我们把它们称为根与系数关系定理.
如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为：AB=====
请你参考以上定理和结论，解答下列问题：
设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)，抛物线的顶点为C，显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时，直接写出b2-4ac的值；
(2)当△ABC为等腰三角形，且∠ACB=120°时，直接写出b2-4ac的值；
(3)设抛物线y=x2+mx+5与x轴的两个交点为A、B，顶点为C，且∠ACB=90°，试问如何平移此抛物线，才能使∠ACB=120°.
25．（10分）在平面直角坐标系中，函数图象上点的横坐标与其纵坐标的和称为点的“坐标和”，而图象上所有点的“坐标和”中的最小值称为图象的“智慧数”．如图：抛物线上有一点，则点的“坐标和”为6，当时，该抛物线的“智慧数”为1．
（1）点在函数的图象上，点的“坐标和”是 ；
（2）求直线的“智慧数”；
（3）若抛物线的顶点横、纵坐标的和是2，求该抛物线的“智慧数”；
（4）设抛物线顶点的横坐标为，且该抛物线的顶点在一次函数的图象上；当时，抛物线的“智慧数”是2，求该抛物线的解析式．
26．（10分）一个不透明的口袋里装有分别标有汉字“魅”、“力”、“宜”、“昌”的四个个球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
（1）若从中任取一个球，球上的汉字刚好是“宜”的概率为多少？
（2）甲同学从中任取一球，记下汉字后放回袋中，然后再从袋中任取一球，请用画树图成列表的方法求出甲同学取出的两个球上的汉字恰能组成“魅力”或“宜昌”的概率p甲；
（3）乙同学从中任取一球，不放回，再从袋中任取一球，请求出乙同学取出的两个球上的汉字恰能组成“魅力”或“宜昌”的概率p乙，并指出p甲、p乙的大小关系．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、A
4、C
5、C
6、B
7、C
8、D
9、C
10、C
二、填空题(每小题3分,共24分)
11、
12、m≤1
13、
14、x≥1且x≠1
15、2
16、⊙O上或⊙O内
17、1．
18、
三、解答题(共66分)
19、（1）；（2），1．
20、（1）；（2）P(这2名同学性别相同) =．
21、（1）；（2）；（3）是，
22、（1）见解析；（2）；（3）
23、（1）28.8；（2）
24、 (1)4；(2)；(3)抛物线向上平移个单位后，向左或向右平移任意个单位都能使得度数由90°变为120°.
25、（1）4；（2）直线“智慧数”等于；（3）抛物线的“智慧数”是；（4）抛物线的解析式为或
26、（1）；（2）；（3） ．