2023-2024学年广东省广州市广州外国语学校数学九年级第一学期期末经典试题含答案

这是一份2023-2024学年广东省广州市广州外国语学校数学九年级第一学期期末经典试题含答案，共9页。试卷主要包含了考生必须保证答题卡的整洁，下列图形，二次函数的图象与轴的交点个数是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．如图，四边形内接于, 为延长线上一点,若，则的度数为（ ）
A．B．C．D．
2．已知正比例函数的图象与反比例函数图象相交于点，下列说法正确的是（ ）
A．反比例函数的解析式是
B．两个函数图象的另一交点坐标为
C．当或时，
D．正比例函数与反比例函数都随的增大而增大
3．用配方法解方程时，配方后所得的方程为（ ）
A．B．C．D．
4．下列图形：①国旗上的五角星，②有一个角为60°的等腰三角形，③一个半径为π的圆，④两条对角线互相垂直平分的四边形，⑤函数y＝的图象，其中既是轴对称又是中心对称的图形有（ ）
A．有1个B．有2个C．有3个D．有4个
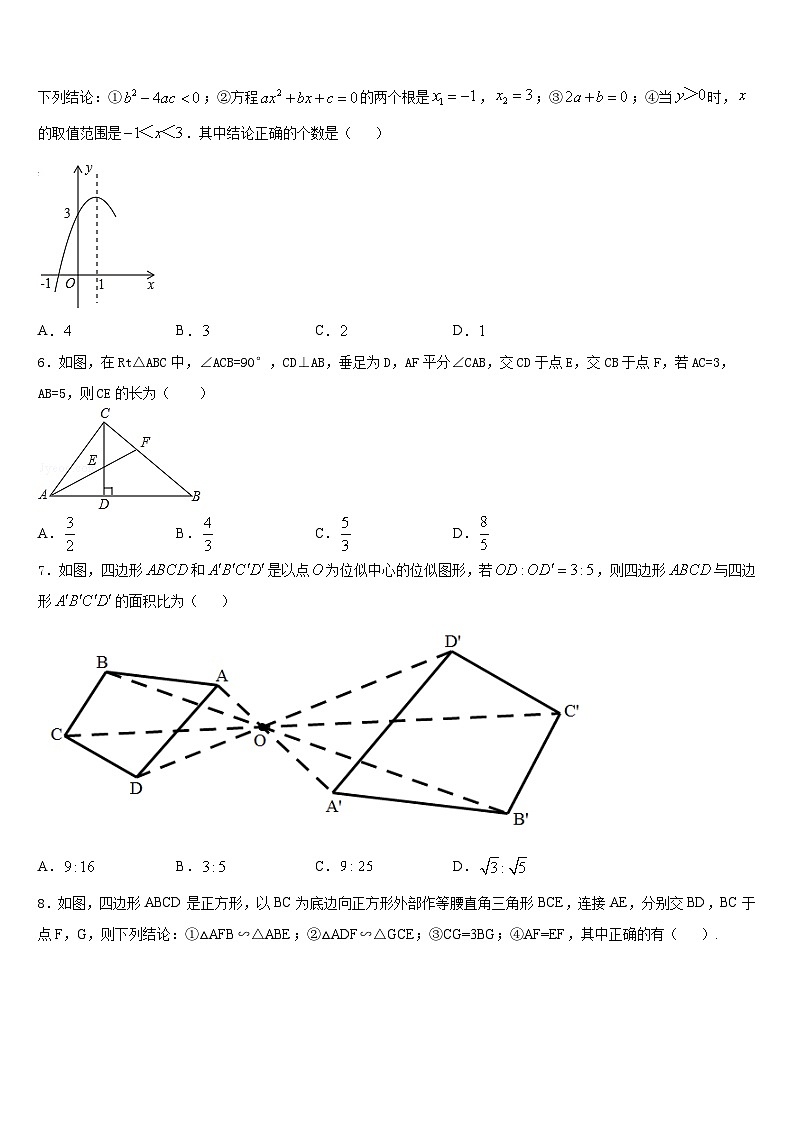
5．如图，抛物线的对称轴为直线，与轴的个交点坐标为，，其部分图象如图所示，下列结论：①；②方程的两个根是，；③；④当时，的取值范围是．其中结论正确的个数是（ ）
A．B．C．D．
6．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F，若AC=3，AB=5，则CE的长为（ ）
A．B．C．D．
7．如图，四边形和是以点为位似中心的位似图形，若，则四边形与四边形的面积比为（ ）
A．B．C．D．
8．如图，四边形ABCD是正方形，以BC为底边向正方形外部作等腰直角三角形BCE，连接AE，分别交BD，BC于点F，G，则下列结论：①△AFB∽△ABE；②△ADF∽△GCE；③CG=3BG；④AF=EF，其中正确的有（ ）.
A．①③B．②④C．①②D．③④
9．如图，在一块斜边长60cm的直角三角形木板（）上截取一个正方形CDEF，点D在边BC上，点E在斜边AB上，点F在边AC上，若CD：CB＝1：3，则这块木板截取正方形CDEF后，剩余部分的面积为（ ）
A．202.5cm2B．320cm2C．400cm2D．405cm2
10．二次函数的图象与轴的交点个数是（ ）
A．2个B．1个C．0个D．不能确定
二、填空题(每小题3分,共24分)
11．已知，且 ，且与的周长和为175 ，则的周长为 _________．
12．如图，公路互相垂直，公路的中点与点被湖隔开，若测得的长为2.4km，则两点间的距离为______km.
13．在矩形中，，以点为圆心，为半径的圆弧交于点，交的延长线于点，连接，则图中阴影部分的面积为：__________．
14．如图，⊙O与直线相离，圆心到直线的距离，，将直线绕点
逆时针旋转后得到的直线刚好与⊙O相切于点，则⊙O的半径= ．
15．在Rt△ABC中，，，，则的值等于__．
16．一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，小文在袋中放入3个白球(每个球除颜色外其余都与红球相同).摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.7左右，则袋中红球约有_____个.
17．如图，在中，，，延长至点，使，则________.
18．如图，在平面直角坐标系中，菱形的边在轴上，与交于点（4，2），反比例函数的图象经过点．若将菱形向左平移个单位，使点落在该反比例函数图象上，则的值为_____________．
三、解答题(共66分)
19．（10分）已知二次函数y＝(x－m)(x＋m＋4)，其中m为常数．
（1）求证：不论m为何值，该二次函数的图像与x轴有公共点．
（2）若A(－1，a)和B(n，b)是该二次函数图像上的两个点，请判断a、b的大小关系．
20．（6分）某鱼塘中养了某种鱼5000条，为了估计该鱼塘中该种鱼的总质量，从鱼塘中捕捞了3次，取得的数据如下：
（1）求样本中平均每条鱼的质量；
（2）估计鱼塘中该种鱼的总质量；
（3）设该种鱼每千克的售价为14元，求出售该种鱼的收入y（元）与出售该种鱼的质量x（kg）之间的函数关系，并估计自变量x的取值范围．
21．（6分）如图1，已知抛物线y＝﹣x2+bx+c交y轴于点A(0，4)，交x轴于点B(4，0)，点P是抛物线上一动点，试过点P作x轴的垂线1，再过点A作1的垂线，垂足为Q，连接AP．
(1)求抛物线的函数表达式和点C的坐标；
(2)若△AQP∽△AOC，求点P的横坐标；
(3)如图2，当点P位于抛物线的对称轴的右侧时，若将△APQ沿AP对折，点Q的对应点为点Q′，请直接写出当点Q′落在坐标轴上时点P的坐标．
22．（8分）如图，△ABC是等腰三角形，且AC=BC，∠ACB=120°，在AB上取一点O，使OB=OC，以O为圆心，OB为半径作圆，过C作CD∥AB交⊙O于点D，连接BD．
（1）猜想AC与⊙O的位置关系，并证明你的猜想；
（2）已知AC=6，求扇形OBC围成的圆锥的底面圆半径．
23．（8分）如图，是的直径，点在的延长线上，平分交于点，且的延长线，垂足为点．
（1）求证：直线是的切线；
（2）若，，求的长．
24．（8分）四张质地相同的卡片如图所示．将卡片洗匀后，背面朝上放置在桌面上．
（1）求随机抽取一张卡片，恰好得到数字2的概率；
（2）小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗？请用列表法或画树状图法说明理由，若认为不公平，请你修改规则，使游戏变得公平．
25．（10分）在平面直角坐标系中（如图），已知二次函数（其中a、b、c是常数，且a≠0）的图像经过点A（0，-3）、B（1，0）、C（3，0），联结AB、AC．
（1）求这个二次函数的解析式；
（2）点D是线段AC上的一点，联结BD，如果，求tan∠DBC的值；
（3）如果点E在该二次函数图像的对称轴上，当AC平分∠BAE时，求点E的坐标．
26．（10分）如图，在锐角△ABC中，小明进行了如下的尺规作图：
①分别以点A、B为圆心，以大于AB的长为半径作弧，两弧分别相交于点P、Q；
②作直线PQ分别交边AB、BC于点E、D．
（1）小明所求作的直线DE是线段AB的 ；
（2）联结AD，AD＝7，sin∠DAC＝，BC＝9，求AC的长．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、D
4、C
5、B
6、A
7、C
8、B
9、C
10、A
二、填空题(每小题3分,共24分)
11、1
12、1.1
13、
14、1．
15、
16、1
17、
18、1
三、解答题(共66分)
19、（1）见解析；（2） ①当n＝－3时，a＝b；②当－3＜n＜－1时，a＞b ；③当n＜－3或n＞－1时，a＜b
20、（1）1.78kg；（2）1kg；（3）y＝14x，0≤x≤1．
21、 (1)y＝﹣x2+3x+4；(﹣1，0)；(2)P的横坐标为或.(3)点P的坐标为(4，0)或(5，﹣6)或(2，6).
22、 (1)见解析;(2).
23、（1）见解析；（2）
24、解：（1）P（抽到2）= ．
（2）不公平，修改规则见解析
25、（1）；（2）；（3）E（2，）
26、（1）线段AB的垂直平分线（或中垂线）；（2）AC＝5．
数量/条
平均每条鱼的质量/kg
第1次捕捞
20
1.6
第2次捕捞
15
2.0
第3次捕捞
15
1.8