2023-2024学年广东省江门市蓬江区数学九上期末联考试题含答案

这是一份2023-2024学年广东省江门市蓬江区数学九上期末联考试题含答案，共7页。试卷主要包含了以为顶点的二次函数是，对于题目“抛物线l1等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1．下列方程中，关于x的一元二次方程是（ ）
A．2x﹣3＝xB．2x+3y＝5C．2x﹣x2＝1D．
2．已知关于x的一元二次方程的一个根为1，则m的值为( )
A．1B．-8C．-7D．7
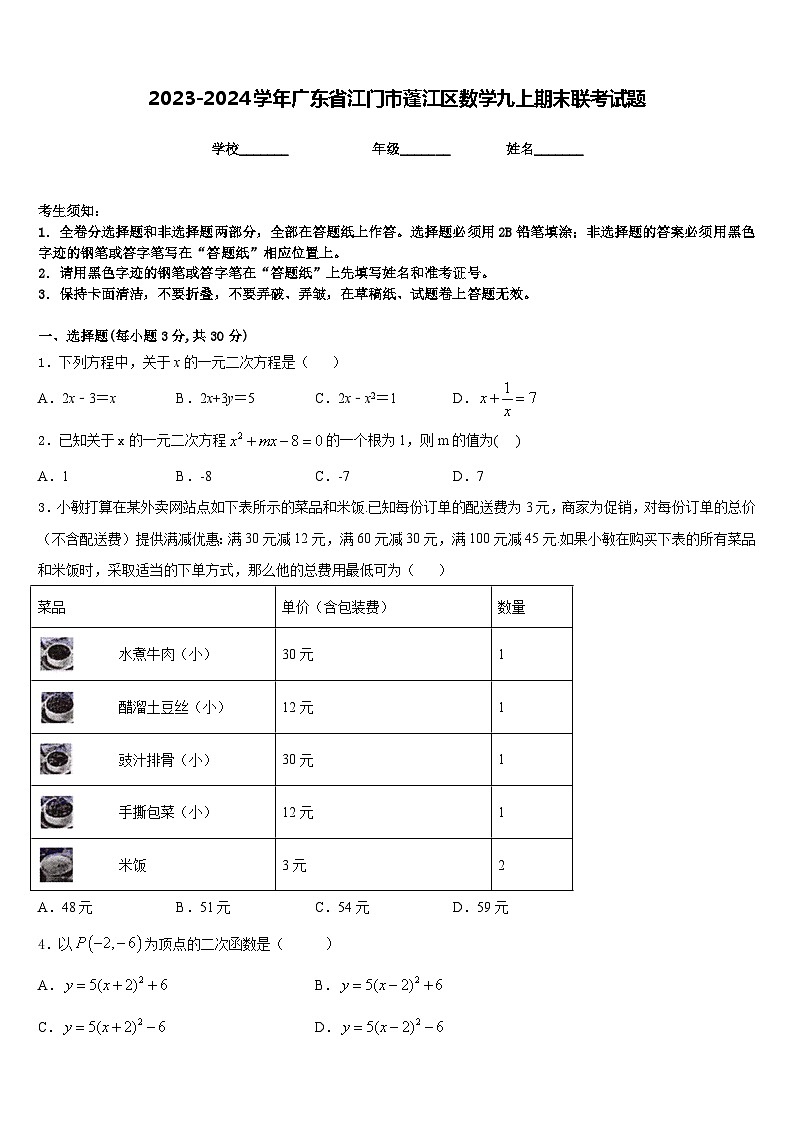
3．小敏打算在某外卖网站点如下表所示的菜品和米饭.已知每份订单的配送费为3元，商家为促销，对每份订单的总价（不含配送费）提供满减优惠：满30元减12元，满60元减30元，满100元减45元.如果小敏在购买下表的所有菜品和米饭时，采取适当的下单方式，那么他的总费用最低可为（ ）
A．48元B．51元C．54元D．59元
4．以为顶点的二次函数是（ ）
A．B．
C．D．
5．一个不透明的袋子中有3个红球和2个黄球，这些球除颜色外完全相同．从袋子中随机摸出一个球，它是黄球的概率为（ ）
A．B．C．D．
6．小明和小华玩“石头、剪子、布”的游戏．若随机出手一次，则小华获胜的概率是（ ）
A．B．C．D．
7．对于题目“抛物线l1：（﹣1＜x≤2）与直线l2：y＝m（m为整数）只有一个交点，确定m的值”；甲的结果是m＝1或m＝2；乙的结果是m＝4，则（ ）
A．只有甲的结果正确
B．只有乙的结果正确
C．甲、乙的结果合起来才正确
D．甲、乙的结果合起来也不正确
8．某次聚会，每两个参加聚会的人都互相握了一次手，有人统计一共握了10次手．求这次聚会的人数是多少？设这次聚会共有人，可列出的方程为（ ）
A．B．C．D．
9．赵州桥的桥拱可以用抛物线的一部分表示，函数关系为，当水面宽度AB为20m时，水面与桥拱顶的高度DO等于（ ）
A．2mB．4mC．10mD．16m
10．已知二次函数y＝ax2+bx+c的图象如图所示，下列结i论：①abc＞1；②b2﹣4ac＞1；③2a+b＝1；④a﹣b+c＜1．其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
二、填空题(每小题3分,共24分)
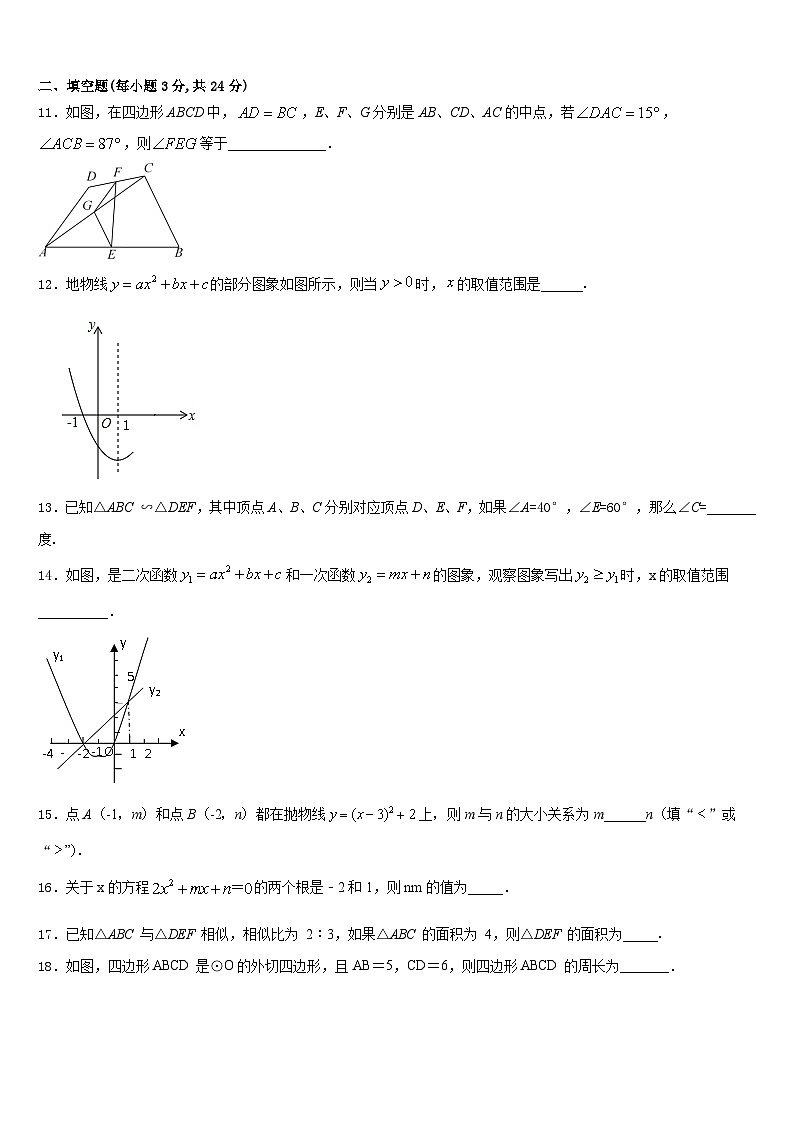
11．如图，在四边形ABCD中，，E、F、G分别是AB、CD、AC的中点，若，，则等于______________．
12．地物线的部分图象如图所示，则当时，的取值范围是______．
13．已知△ABC ∽△DEF，其中顶点A、B、C分别对应顶点D、E、F，如果∠A=40°，∠E=60°，那么∠C=_______度.
14．如图，是二次函数和一次函数的图象，观察图象写出时，x的取值范围__________．
15．点A（-1，m）和点B（-2，n）都在抛物线上，则m与n的大小关系为m______n（填“”或“”）．
16．关于x的方程的两个根是﹣2和1，则nm的值为_____．
17．已知△ABC 与△DEF 相似，相似比为 2：3，如果△ABC 的面积为 4，则△DEF 的面积为_____．
18．如图，四边形ABCD是⊙O的外切四边形，且AB＝5，CD＝6，则四边形ABCD的周长为_______．
三、解答题(共66分)
19．（10分）如图，平面直角坐标中，把矩形OABC沿对角线OB所在的直线折叠，点A落在点D处，OD与BC交于点E．OA、OC的长是关于x的一元二次方程x2﹣9x+18＝0的两个根（OA＞OC）．
（1）求A、C的坐标．
（2）直接写出点E的坐标，并求出过点A、E的直线函数关系式．
（3）点F是x轴上一点，在坐标平面内是否存在点P，使以点O、B、P、F为顶点的四边形为菱形？若存在请直接写出P点坐标；若不存在，请说明理由．
20．（6分）用适当的方法解下列一元二次方程：
（1）2x2＋4x－1＝0；（2）(y＋2)2－(3y－1)2＝0.
21．（6分）甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示．游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．
（1）用列表法（或画树状图）求甲获胜的概率；
（2）你认为这个游戏规则对双方公平吗？请简要说明理由．
22．（8分）某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元，市场调查发现，这种双肩包每天的销售量(个)与y销售单价x(元)有如下关系:，设这种双肩包每天的销售利润为w元．
(1)这种双肩包销售单价定为多少元时，每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元?
23．（8分）如图，在平面直角坐标系中，抛物线y＝﹣x1+1x+a交x轴于点A，B，交y轴于点C，点A的横坐标为﹣1．
（1）求抛物线的对称轴和函数表达式．
（1）连结BC线段，BC上有一点D，过点D作x轴的平行线交抛物线于点E，F，若EF＝6，求点D的坐标．
24．（8分）用适当方法解下列方程．
(1) (2)
25．（10分）（1）；
（2）已知一个几何体的三视图如图所示，求该几何体的体积．
26．（10分）如图，在正方形中，点在边上，过点作于，且.
（1）若，求正方形的周长；
（2）若，求正方形的面积.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、C
4、C
5、B
6、A
7、C
8、D
9、B
10、C
二、填空题(每小题3分,共24分)
11、36°
12、或
13、80
14、．
15、＜.
16、﹣1
17、1
18、1
三、解答题(共66分)
19、（1）A（6，0），C（0，3）；（2）E（，3），y＝﹣x+；（3）满足条件的点P坐标为（6﹣3，3）或（6+3，3）或（，3）或（6，﹣3）．
20、（1）x1＝－1＋，x2＝－1－；（2）y1＝－，y2＝.
21、 (1) ；（2）公平，理由见解析
22、（1）当x=45时，w有最大值，最大值是225;（2）获得200元的销售利润，销售单价应定为40元
23、（1）y＝﹣x1+1x+6；对称轴为x=1；（1）点D的坐标为（1.5，3.5）．
24、（1），；（2），
25、（1）； （2）几何体的体积是1.
26、（1）；（2）.
菜品
单价（含包装费）
数量
水煮牛肉（小）
30元
1
醋溜土豆丝（小）
12元
1
豉汁排骨（小）
30元
1
手撕包菜（小）
12元
1
米饭
3元
2