2023-2024学年广西省来宾市九年级数学第一学期期末达标测试试题含答案

这是一份2023-2024学年广西省来宾市九年级数学第一学期期末达标测试试题含答案，共7页。试卷主要包含了二次函数y＝ax2+bx+c，计算的结果是，已知函数是的图像过点，则的值为，如图，以等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．下列事件是随机事件的是（ ）
A．三角形内角和为度B．测量某天的最低气温，结果为
C．买一张彩票，中奖D．太阳从东方升起
2．等腰三角形底角与顶角之间的函数关系是（ ）
A．正比例函数B．一次函数C．反比例函数D．二次函数
3．二次三项式配方的结果是（ ）
A．B．
C．D．
4． “割圆术”是我国古代的一位伟大的数学家刘徽首创的，该割圆术，就是通过不断倍增圆内接正多边形的边数来求出圆周率的一种方法，某同学在学习“割圆术”的过程中，画了一个如图所示的圆的内接正十二边形，若该圆的半径为1，则这个圆的内接正十二边形的面积为（ ）．
A．1B．3C．3.1D．3.14
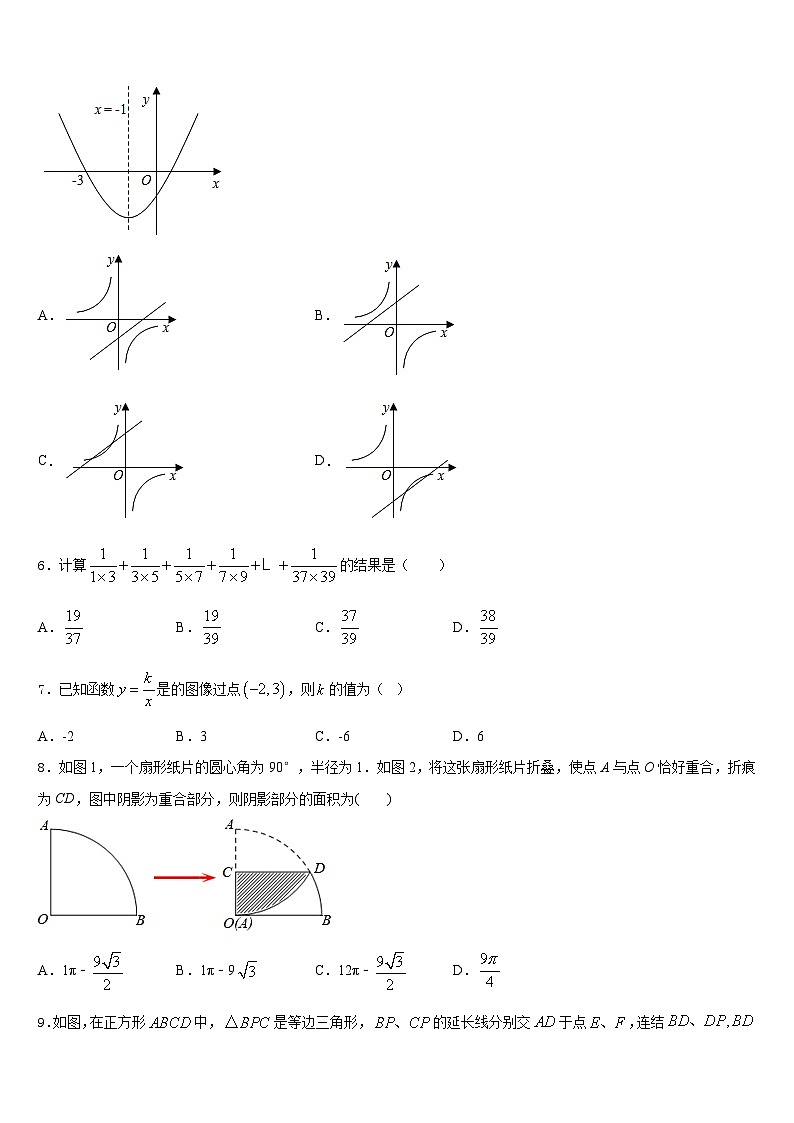
5．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax﹣2b（a≠0）与反比例函数y＝（c≠0）在同一平面直角坐标系中的图象大致是（ ）
A．B．
C．D．
6．计算的结果是（ ）
A．B．C．D．
7．已知函数是的图像过点，则的值为（ ）
A．-2B．3C．-6D．6
8．如图1，一个扇形纸片的圆心角为90°，半径为1．如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为( )
A．1π﹣B．1π﹣9C．12π﹣D．
9．如图，在正方形中，是等边三角形，的延长线分别交于点，连结与相交于点H．给出下列结论，
①△ABE≌△DCF；②△DPH是等腰三角形；③；④，
其中正确结论的个数是（ ）
A．B．C．D．
10．如图，以（1，-4）为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点，则一元二次方程ax2+bx+c=0的正数解的范围是（ ）
A．2＜x＜3B．3＜x＜4C．4＜x＜5D．5＜x＜6
二、填空题(每小题3分,共24分)
11．如图AC，BD是⊙O的两条直径，首位顺次连接A，B，C，D得到四边形ABCD，若AD=3，∠BAC=30°，则图中阴影部分的面积是______．
12．如图，AB是⊙O的直径，AC是⊙O的切线，连结OC交⊙O于点D，连结BD，∠C＝30°，则∠ABD的度数是_____°．
13．等边三角形ABC绕着它的中心，至少旋转______度才能与它本身重合
14．关于x的一元二次方程x2+nx﹣12＝0的一个解为x＝3，则n＝_____．
15．二次函数y=x2﹣2x+3图象的顶点坐标为_____．
16．方程（x﹣1）2=4的解为_____．
17．在△ABC中，∠ABC=90°，已知AB=3，BC=4，点Q是线段AC上的一个动点，过点Q作AC的垂线交直线AB于点P，当△PQB为等腰三角形时，线段AP的长为_____．
18． “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FE⊥AD，EG=15里，HG经过A点，则FH=__里.
三、解答题(共66分)
19．（10分）如图 ，梯形ABCD中，，点在上，连与的延长线交于点G．
（1）求证：；
（2）当点F是BC的中点时，过F作交于点，若，求的长．
20．（6分）在2019年国庆期间，王叔叔的服装店进回一种女装，进价为400元，他首先在进价的基础上增加100元，由于销量非常好，他又连续两次涨价，结果标价比进价的2倍还多45元，求王叔叔这两次涨价的平均增长率是百分之多少？
21．（6分）如图，⊙O的直径AB为10cm，弦BC为6cm，D，E分别是∠ACB的平分线与⊙O，直径AB的交点，P为AB延长线上一点，且PC＝PE．
（1）求AC、AD的长；
（2）试判断直线PC与⊙O的位置关系，并说明理由．
22．（8分）如图1，抛物线平移后过点A（8，,0）和原点，顶点为B，对称轴与轴相交于点C，与原抛物线相交于点D．
（1）求平移后抛物线的解析式并直接写出阴影部分的面积；
（2）如图2，直线AB与轴相交于点P，点M为线段OA上一动点，为直角，边MN与AP相交于点N，设，试探求：
①为何值时为等腰三角形；
②为何值时线段PN的长度最小，最小长度是多少．

23．（8分）如图，在菱形中， 点是边上一点，延长至点,使， 连接求证:．
24．（8分）某学校为了美化校园环境，向园林公司购买一批树苗.公司规定：若购买树苗不超过60棵，则每棵树售价120元；若购买树苗超过60棵，则每增加1棵，每棵树售价均降低0.5元，且每棵树苗的售价降到100元后，不管购买多少棵树苗，每棵售价均为100元.
（1）若该学校购买50棵树苗，求这所学校需向园林公司支付的树苗款；
（2）若该学校向园林公司支付树苗款8800元，求这所学校购买了多少棵树苗.
25．（10分）伴随经济发展和生活水平的日益提高，水果超市如雨后春笋般兴起．万松园一水果超市从外地购进一种水果，其进货成本是每吨0.4万元，根据市场调查，这种水果在市场上的销售量y（吨）与销售价x（万元）之间的函数关系为y＝-x＋2.6
（1）当每吨销售价为多少万元时，销售利润为0.96万元？
（2）当每吨销售价为多少万元时利润最大？并求出最大利润是多少？
26．（10分）某地2016年为做好“精准扶贫”，投入资金1000万元用于异地安置，并规划投入资金逐年增加，2018年在2016年的基础上增加投入资金1250万元．
（1）从2016年到2018年，该地投入异地安置资金的年平均增长率为多少？
（2）在2018年异地安置的具体实施中，该地计划投入资金不低于400万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天补助5元，按租房400天计算，试求今年该地至少有多少户享受到优先搬迁租房奖励？
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、B
4、B
5、D
6、B
7、C
8、A
9、A
10、C
二、填空题(每小题3分,共24分)
11、
12、30°
13、120
14、1
15、（1，2）．
16、x1=3，x2=﹣1
17、或1．
18、1.1
三、解答题(共66分)
19、（1）证明见解析；（2）2cm
20、
21、（1）AC＝8cm；AD＝cm；（2）PC与圆⊙O相切，理由见解析
22、（1）平移后抛物线的解析式，= 12；（2）①，②当＝3时，PN取最小值为．
23、见解析．
24、（1）这所学校需向园林公司支付的树苗款为6000元；（2）这所中学购买了80棵树苗.
25、（1）当每吨销售价为1万元或2万元时，销售利润为 0.96万元；（2）每吨销售价为1.5万元时，销售利润最大，最大利润是1.21万元．
26、（1）从2016年到2018年，该地投入异地安置资金的年平均增长率为50%；（2）今年该地至少有1400户享受到优先搬迁租房奖励．