
2023-2024学年江苏省扬州市仪征市、高邮市九上数学期末联考试题含答案
展开学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.已知线段MN=4cm,P是线段MN的黄金分割点,MP>NP,那么线段MP的长度等于( )
A.(2+2)cmB.(2﹣2)cmC.(+1)cmD.(﹣1)cm
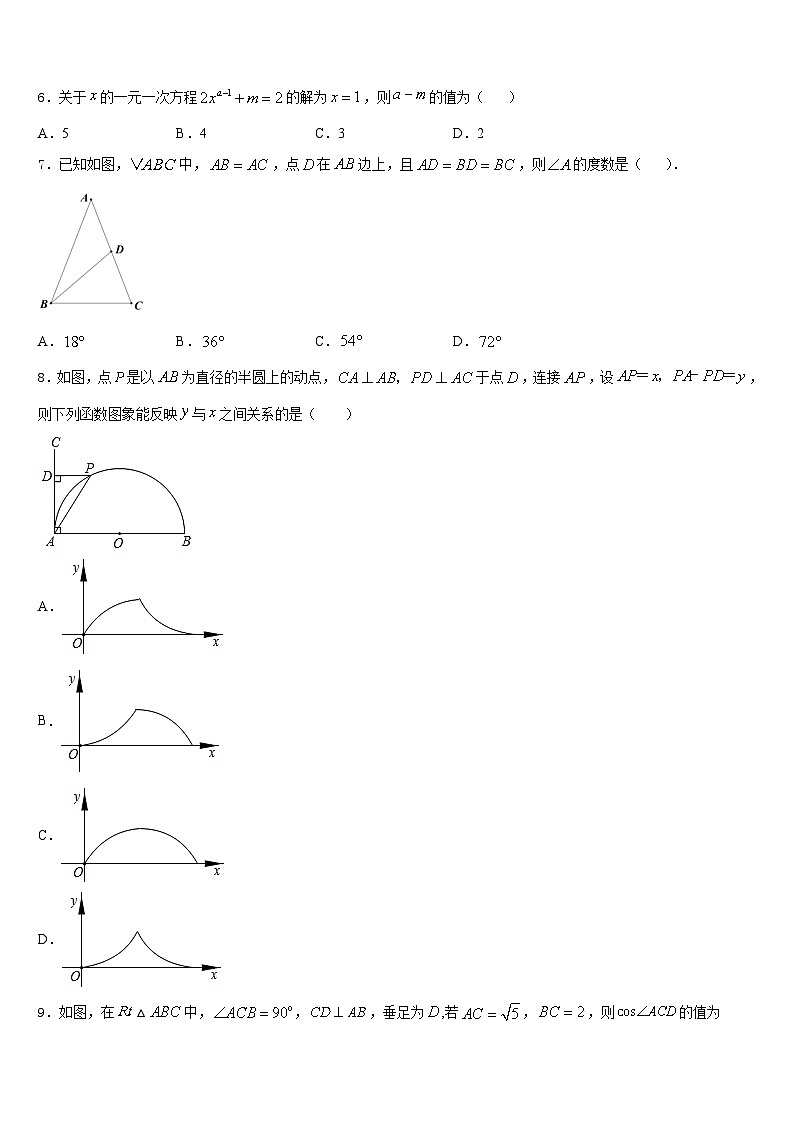
2.如图,小颖身高为160cm,在阳光下影长AB=240cm,当她走到距离墙角(点D)150cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为( )
A.50B.60C.70D.80
3.数据4,3,5,3,6,3,4的众数和中位数是( )
A.3,4B.3,5C.4,3D.4,5
4.如图所示,△的顶点是正方形网格的格点,则的值是( )
A.B.C.D.
5.体育课上,某班两名同学分别进行5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的( )
A.平均数B.频数C.中位数D.方差
6.关于的一元一次方程的解为,则的值为( )
A.5B.4C.3D.2
7.已知如图,中,,点在边上,且,则的度数是( ).
A.B.C.D.
8.如图,点是以为直径的半圆上的动点,于点,连接,设,则下列函数图象能反映与之间关系的是( )
A.
B.
C.
D.
9.如图,在△中,,,垂足为,若,,则的值为( )
A.B.
C.D.
10.要使有意义,则x的取值范围为( )
A.x≤0B.x≥-1C.x≥0D.x≤-1
二、填空题(每小题3分,共24分)
11.如图,扇形ABC的圆心角为90°,半径为6,将扇形ABC绕A点逆时针旋转得到扇形ADE,点B、C的对应点分别为点D、E,若点D刚好落在上,则阴影部分的面积为_____.
12.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
13.已知抛物线的对称轴是直线,其部分图象如图所示,下列说法中:①;②;③;④当时,,正确的是_____(填写序号).
14.如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=________.
15.若关于x的方程x2-kx+9=0(k为常数)有两个相等的实数根,则k=_____.
16.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.
17.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,若AD=3,CE=5,则CD等于_____.
18.若一个正六边形的周长为24,则该正六边形的面积为 ▲ .
三、解答题(共66分)
19.(10分)解方程:
(1)x2﹣4x+2=0;
(2)
20.(6分)一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量(件与销售价(元/件)之间的函数关系如图所示.
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)求每天的销售利润W(元与销售价(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
21.(6分)如图,在中,,,夹边的长为6,求的面积.
22.(8分)已知反比例函数的图象经过点A(2,6).
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于哪些象限?y随x的增大如何变化?
(3)点B(3,4),C(5,2),D(,)是否在这个函数图象上?为什么?
23.(8分)方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)作出△ABC关于y轴对称的,并写出的坐标;
(2)作出△ABC绕点O逆时针旋转90°后得到的,并求出所经过的路径长.
24.(8分)如图,已知抛物线与轴相交于、两点,与轴相交于点,若已知点的坐标为.
(1)求抛物线的解析式;
(2)求线段所在直线的解析式;
(3)在抛物线的对称轴上是否存在点,使为等腰三角形?若存在,求出符合条件的点坐标;若不存在,请说明理由.
25.(10分)小王去年开了一家微店,今年1月份开始盈利,2月份盈利2400元,4月份盈利达到3456元,且从2月份到4月份,每月盈利的平均增长率相同,试求每月盈利的平均增长率.
26.(10分)我县寿源壹号楼盘准备以每平方米元均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望,房地产开发商为了加快资金周转,对价格进行两次下调后,决定以每平方米元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘均价购买一套平方米的住房,开发商给予以下两种优惠方案供选择:
①打折销售;
②不打折,一次性送装修费每平方米元.
试问哪种方案更优惠?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、A
4、B
5、D
6、D
7、B
8、C
9、D
10、B
二、填空题(每小题3分,共24分)
11、3π+9.
12、这个“果圆”被y轴截得的线段CD的长3+.
13、①③④.
14、65°
15、±1
16、
17、
18、
三、解答题(共66分)
19、(1);(1)x1=﹣3,x1=1.
20、(1) (2),,144元
21、△ABC的面积是.
22、 (1);(2)这个函数的图象位于第一、三象限,在每一个象限内,y随x的增大而减小;(3)点B,D在函数的图象上,点C不在这个函数图象上.
23、 (1)作图详见解析;(﹣5,﹣4);(2)作图详见解析;.
24、(1);(2);(3)存在,(2,2)或(2,-2)或(2,0)或(2,)
25、
26、(1)10%;(2)选择方案①更优惠.
江苏省扬州市仪征市、高邮市2023-2024学年数学九年级第一学期期末学业质量监测试题含答案: 这是一份江苏省扬州市仪征市、高邮市2023-2024学年数学九年级第一学期期末学业质量监测试题含答案,共7页。试卷主要包含了如图,在中,,,则的值是,在下列各式中,运算结果正确的是,已知甲、乙两地相距100,如果,那么下列各式中不成立的是等内容,欢迎下载使用。
2023-2024学年江苏省扬州市高邮市汪曾祺学校九上数学期末复习检测试题含答案: 这是一份2023-2024学年江苏省扬州市高邮市汪曾祺学校九上数学期末复习检测试题含答案,共9页。试卷主要包含了如图,点A,如图所示的几何体的左视图为等内容,欢迎下载使用。
2023-2024学年江苏扬州市仪征市九上数学期末检测试题含答案: 这是一份2023-2024学年江苏扬州市仪征市九上数学期末检测试题含答案,共8页。












